动态规划题目分析和解法

在正式介绍动态规划之前，应当先回顾了分治，回溯和递归。在课上讲到，“动态规划”和前面三者其实没有本质区别，都是把问题进行拆分，寻找规律。比如分治其实是递归的特殊形式，很多题目子问题都是有自相似性的，关键在于怎么把大问题分解成小的子问题。

 

养成数学归纳法思想，也就是先把基础条件想明白然后解决，比如n=1怎么样，n=2的时候又怎么样，然后推导到n和n+1的情况。数学归纳法的思想好比是爆竹，想要整串都能爆炸，我们需要推导所有的最后都能爆炸。

 

动态规划具体是什么意思？有一个例子其实很生动。比如我们在纸上写了很多个”1+1+1+1+1…”，第一眼看过去，谁都不能知道到底写了多少个1.但是如果我们已经计算好了比如之前一共写了8个1，那么只要再写一个1，我们马上就知道现在一共写了9个1，这就是动态规划。动态规划是一个能够让我们“记忆”之前的成果并且把它们运用在后面的运算中的一个方法，能够让程序“记住”之前所得到的答案。动态规划可以说是用空间换时间的一种方式。

 

对于一个动态规划问题，我们往往需要从两个方面进行考虑，即：找出问题之间的联系以及记录答案。这里的难点实际是找出问题之间的联系，因为记录答案可以用比较简单的数据结构顺带完成。

 

解决动态规划问题一般需要四个步骤：

• 问题拆解，找到问题之间的具体联系
• 状态定义
• 递推方程推导
• 代码实现

 

上述步骤中前两步是最关键的。如果前两步骤顺利完成，后面递推方程的推导是非常简单的。尤其对于面试题，只要找到了合适的状态定义，递推方程往往不会很难，竞赛的话递推方程就可能比较难了。

 

状态定义其实是需要思考在解决一个问题的时候，我们都做了什么事情，然后得出了什么样的答案。对于这个问题，当前问题的答案就是当前的状态。经过了前面两句话的拆解，可以发现两个相邻的问题的联系其实是：

后一个问题的答案 = 前一个问题的答案+1

这里，状态的每次变化就是+1.

 

定义好了状态递推方程就可以变得非常简单。

 

动态规划的四步其实是互相递进的，状态的定义(第二步)离不开问题的拆解(第一步)、递推方程推导(第三步)离不开状态的定义(第二步)，最后的代码实现(第三步)的核心其实就是递推方程(第四步)。

 

LeetCode上面有一些很经典的问题.

 

第70题爬楼梯。

我们可以按照上面的四步进行分析：

1. 问题拆解

我们应当习惯用自底向上的思路方式去做（超哥推荐的），也就是从终点开始想。如果我们要到达第n个台阶，按照题意我们会先到达第n-1或者底n-2级台阶。因此第n个问题可以拆解成第n-1和n-2个子问题，第n-1和n-2又可以继续往下拆，直到第0个问题，也就是上楼梯的起点。

 

1. 状态定义

在问题拆解的时候已经提到了，第n个楼梯会和第n-1和第n-2个楼梯有关联。而两者具体的联系是什么呢？可以这样思考，第n-1个问题中的答案其实是从起点到达第n-1个楼梯的路径总数，n-2同理。而从第n-1个楼梯可以到达第n个台阶，从第n-2个也可以。而且从第n-1到达第n级台阶与从n-2到达第n级台阶，这两者之间的路径不可能有重复。因此我们可以把第i个状态定义为：“从起点到达第i个楼梯的路径总数”，状态之间的联系其实是相加的关系。

1. 递推方程

只要有了正确靠谱的状态定义，递推方程并不难得到。

 

因为在“状态定义”中我们已经定义好了状态，也知道第i个状态可以由第i-1个状态和第i-2个状态通过相加得到，因此递推方程可以得到：

dp[i]=dp[i-1]+dp[i-2]

1. 代码实现

在递推方程中可以看到，我们需要有一个类似“空集”的初始值来方便我们计算。这个起始位置是不用考虑真正用于计算的第一个情况的。所以这里的爬楼梯问题的初始值是不需要移动的位置：dp[0]=0，第1层楼梯只能从起始位置到达，因此dp[1]=1，第2层楼梯可以从起始位置和初始位置到达，因此dp[2]=2，有了这些初始值，后面就可以用递推方法得到。

 

注意，在代码实现的时候，可以不需要和第二步分析状态定义的时候用自底向上的方式。

第二道题，LeetCode120，三角形最小路径和

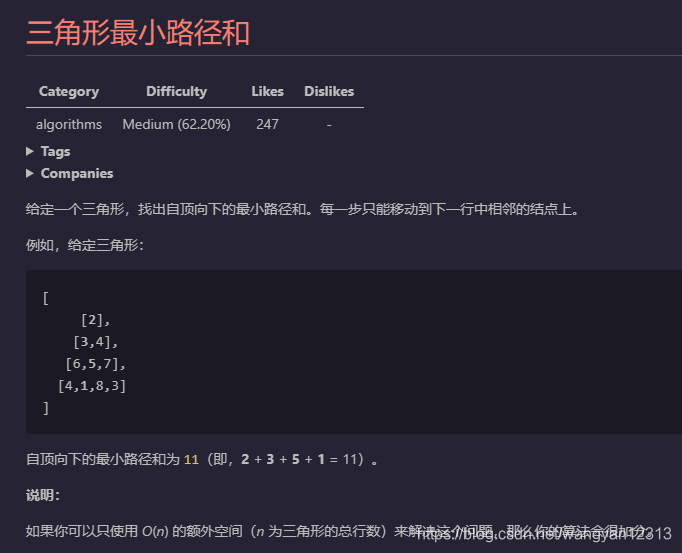
用四个步骤进行分析：

1. 问题拆解

这里要求出最小的路径和， 路径是这里分析的重点，路径是由一个个元素组成的，和之前爬楼梯类似，[i][j]可以看做是位置元素。经过这个位置元素，肯定要经过[i-1][j]或者[i][j-1]，因此经过一个元素的路径可以通过这个元素上面的一个或者两个元素的路径的和得到。

1. 状态定义

状态的定义一般会和问题需要求解的答案联系在一起，这里其实有两种方式，一种是考虑路径从上到下，另一种是考虑路径从下到上。因为元素本身不会变，所以路径的方向不同也不会影响最后求得的路径和，如果是从上到下，你会发现，在考虑下面元素的时候，其实元素的路径只会从[i-1][j]获得，每行当中的最后一个元素的路径只会从[i-1][j-1]获得，但是中间的所有元素的值的获得有规律可寻么？没有，所以从上到下很难实现一个统一的公式。

 

因此我们考虑从下到上的方式，状态的定义就变成了“最后一行元素到当前元素的最小路径和”，对于[0][0]这个元素来说，它的内容就是我们的最终答案。

1. 递推方程

已经定义了状态，所以可以得到递推方程：

dp[i][j]=Math.min(dp[i+1][j],dp[i+1][j+1])+triangle[i][j]

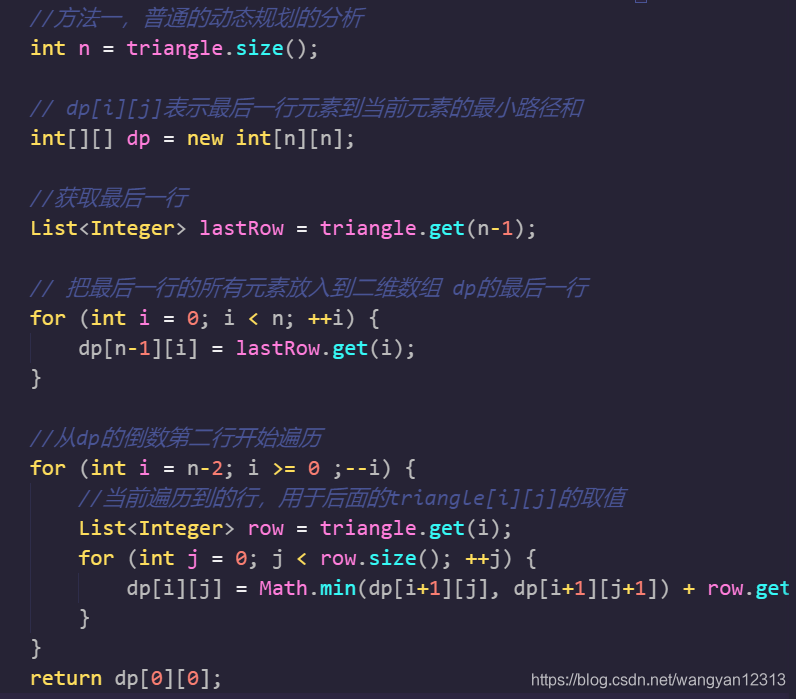
1. 代码实现

这里初始化时，我们需要将最后一行的元素填入到状态数组中，然后就是按照前面的分析策略，从下到上计算即可。

 

事实上在看了很多道动态规划的题目之后我有这样的发现，虽然动态规划理论上主要是通过空间换时间，但是很多时候，问题的维度是二维的时候，往往可以考虑优化成一维空间来解决。而一维空间的问题，往往可以优化成常数级空间来解决。

 

曾经在72题解中LeetCode题解中看到某位同学使用动态规划对自己微信推送进行修改的经历，突然发现这种情景竟然可以如此切合实际……