AI算力基础 -- MIT课程《Understanding Deep Neural Networks》

原创 已于 2022-05-15 18:07:55 修改 · 2.3k 阅读 · 17 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#编码学 #深度学习 #计算机视觉

于 2021-11-28 18:22:36 首次发布
本文介绍了深度神经网络在CPU/GPU平台上的高效处理方法，如矩阵乘法优化、FFT/Strassen/Winograd转换，以及针对稀疏性和精度降低的算法设计。章节详细探讨了批处理大小、数据重用、算法与硬件协同设计，涵盖了深度卷积、灵活性和可扩展性，以及其他平台如DNN加速器和新兴技术。

阅读总结

深度神经网络的高效处理（硬件）《Efficient Processing of Deep Neural Networks》读书笔记
原书：《Efficient Processing of Deep Neural Networks》Vivienne Sze, Yu-Hsin Chen, Tien-Ju Yang, Joel S. Emer（Morgan&Claypool Publishers - Synthesis Lectures On Computer Architecture）出版时间：Jun 2020
作者 MIT Vivienne Sze.

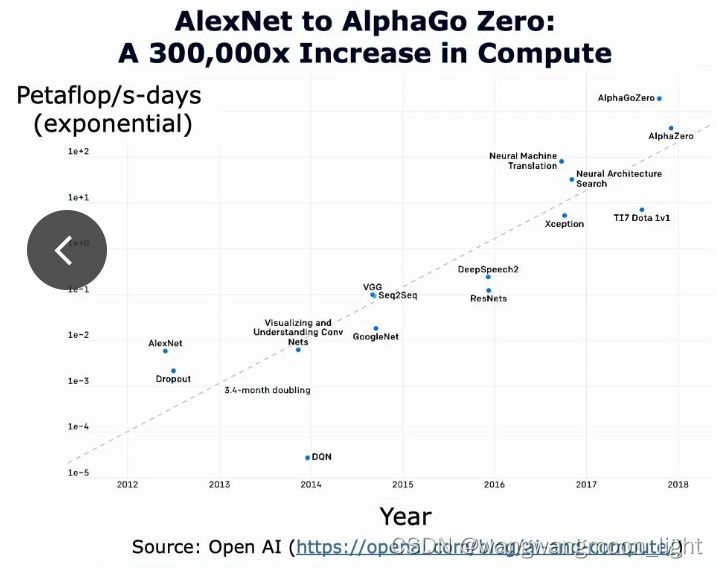
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
Batch Size
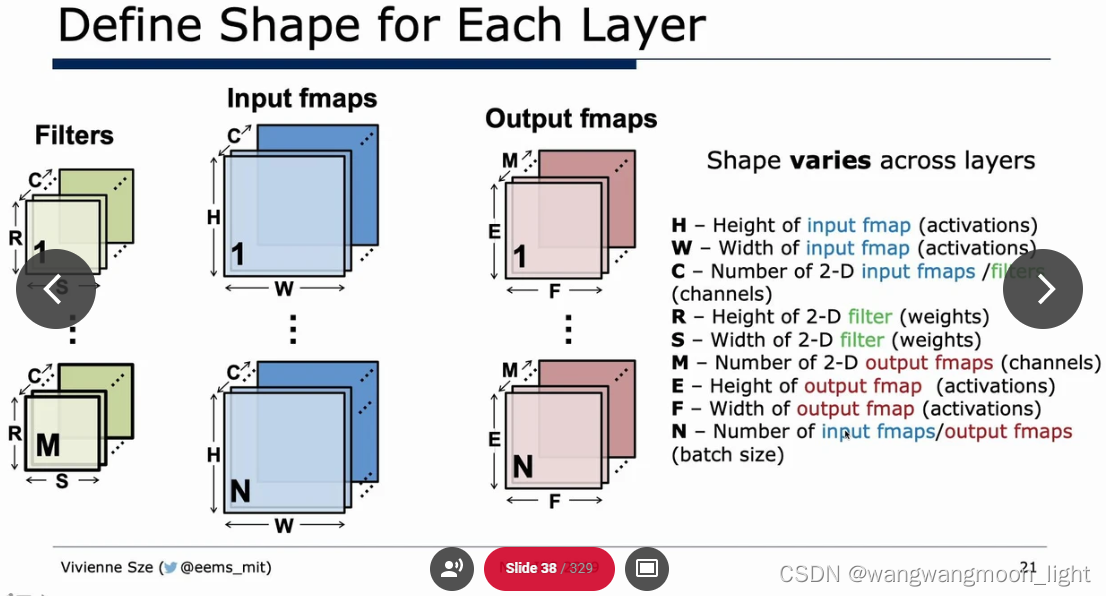
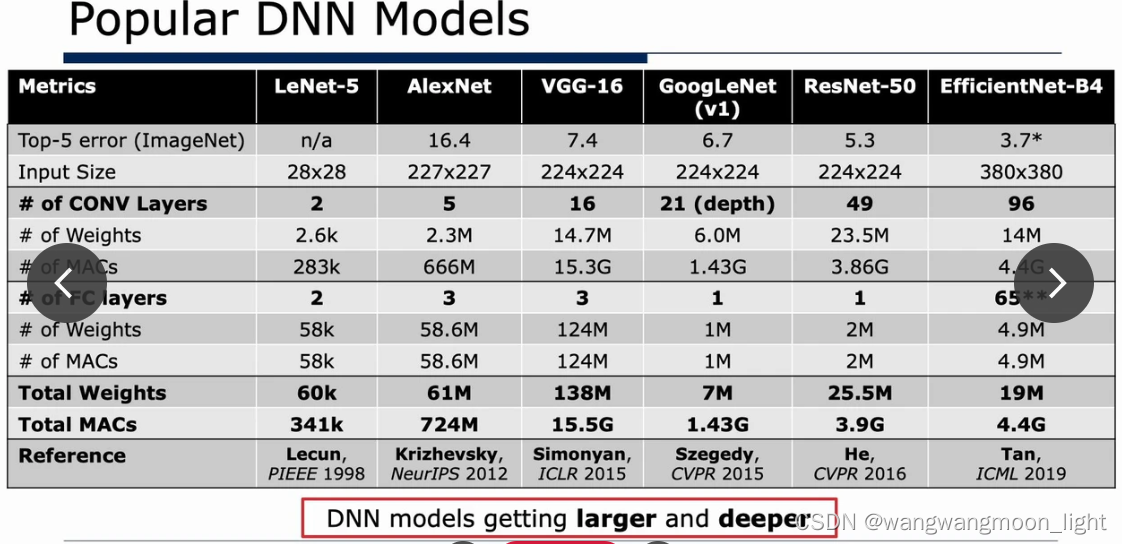
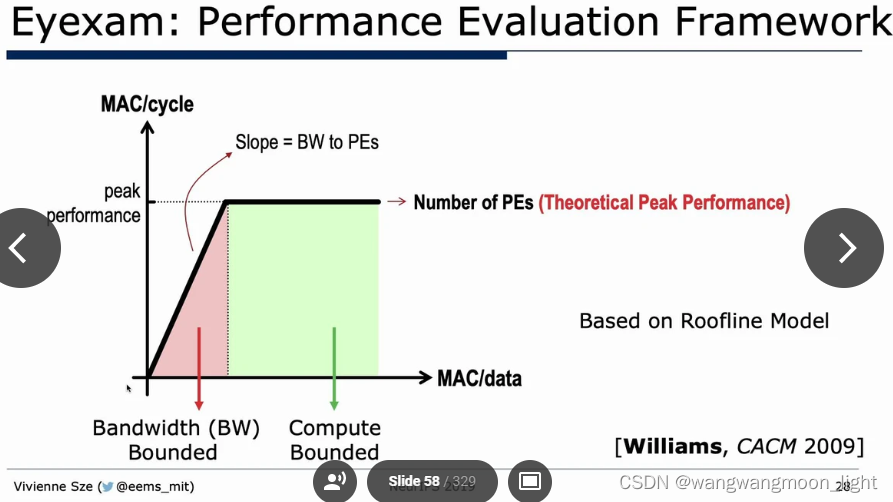
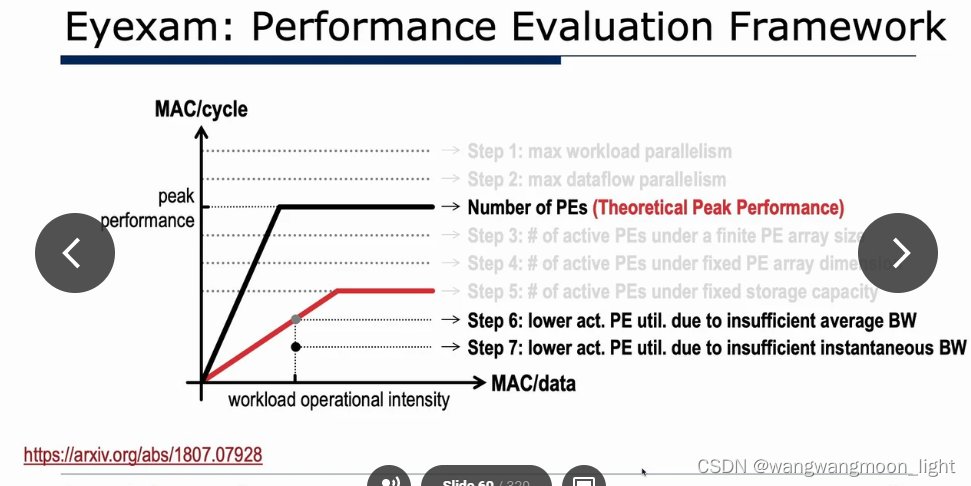
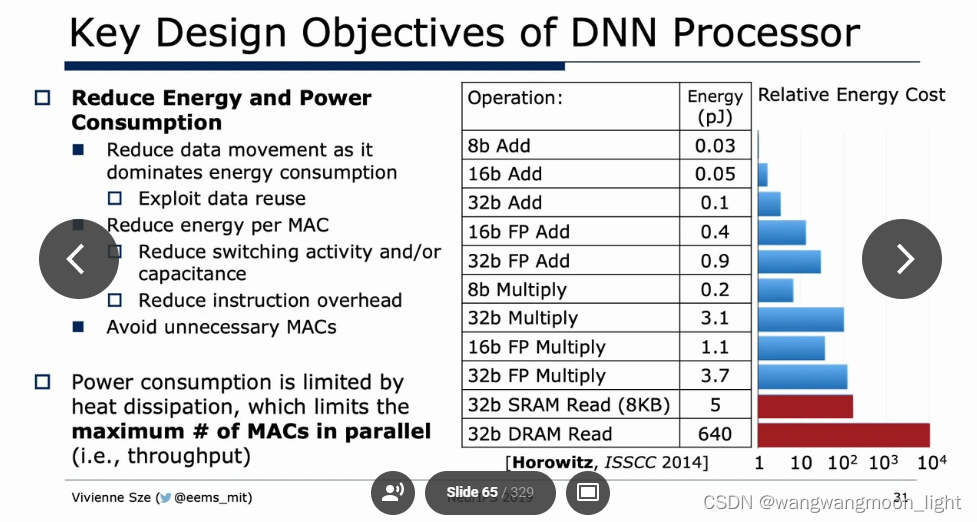
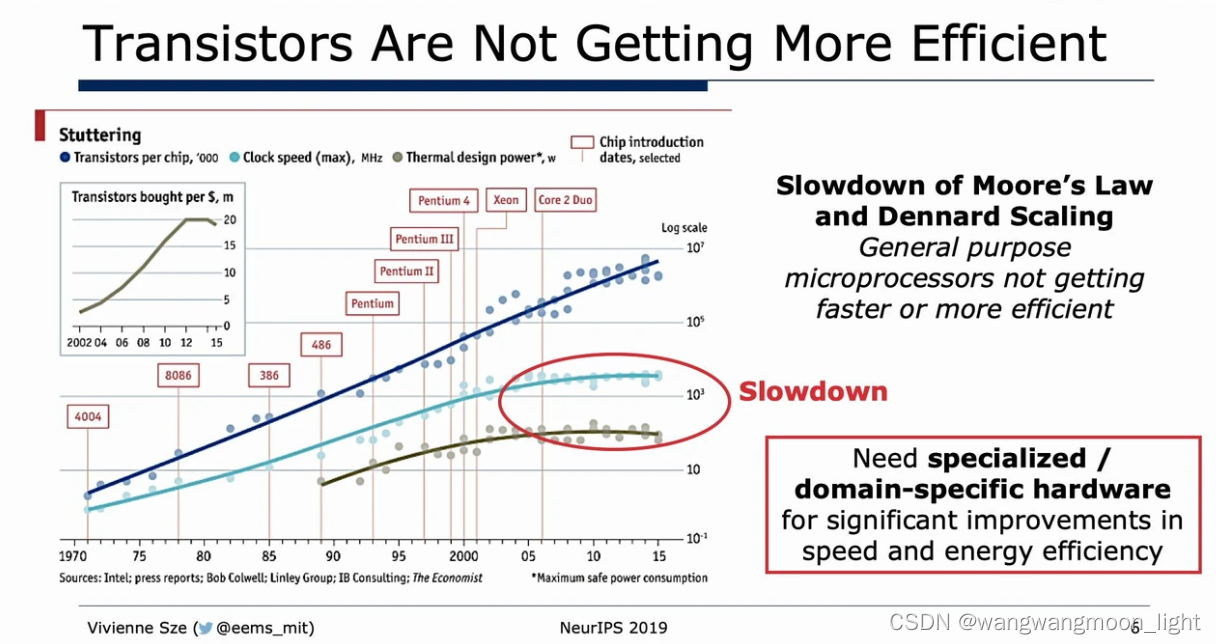
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

一、CPU && GPU Platform

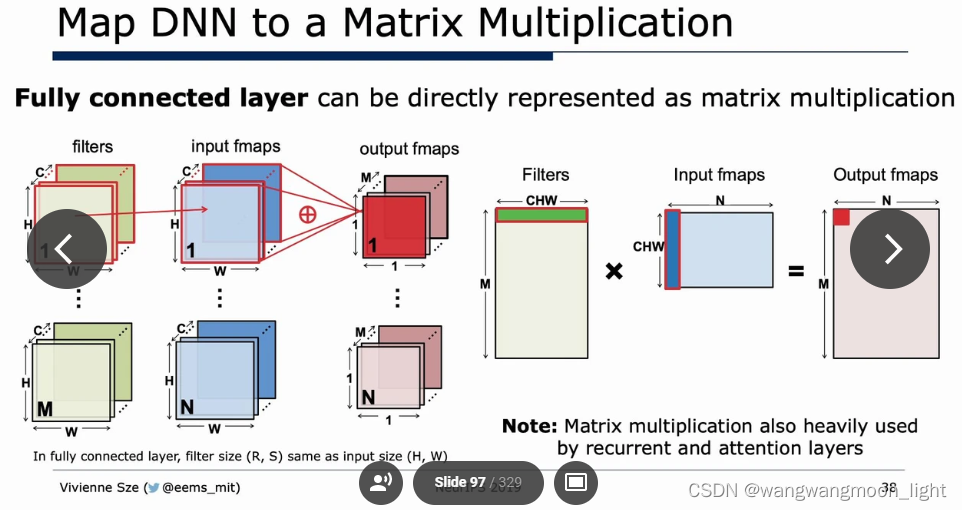
在这里插入图片描述
全连接层可以直接转为矩阵乘：
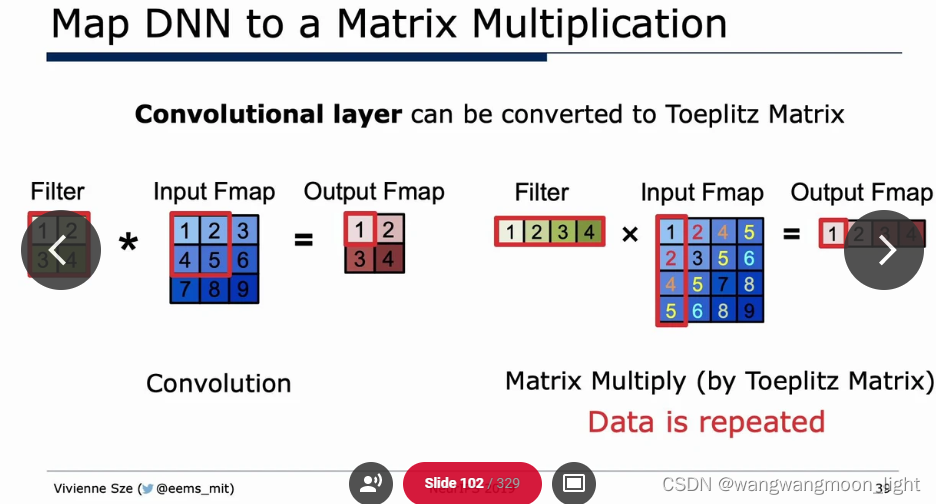
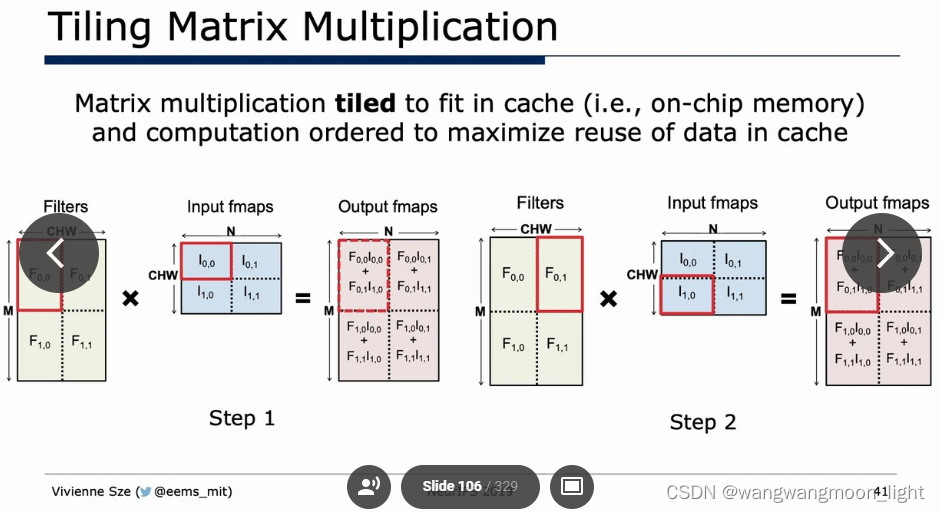
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
高斯算法：
在这里插入图片描述
FFT/Strassen/Winograd：
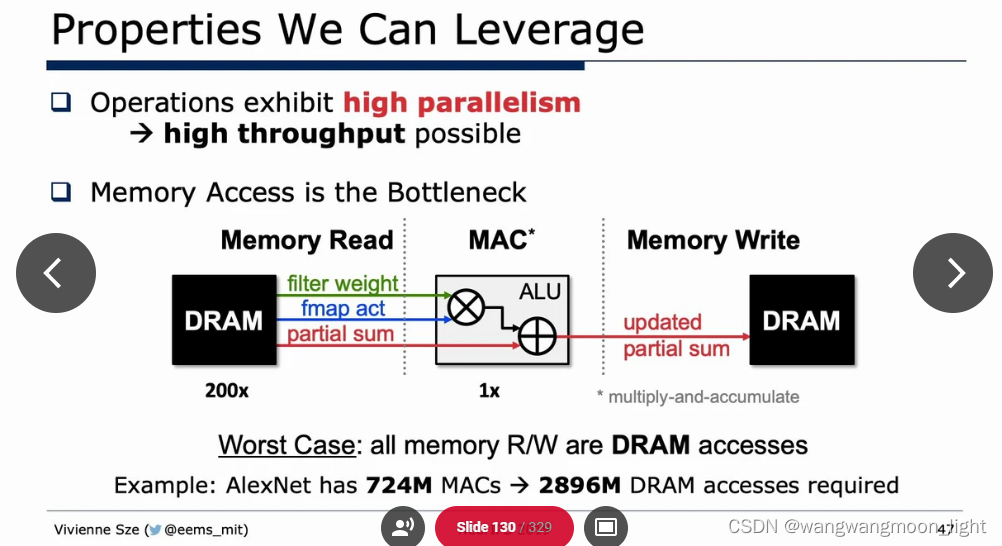
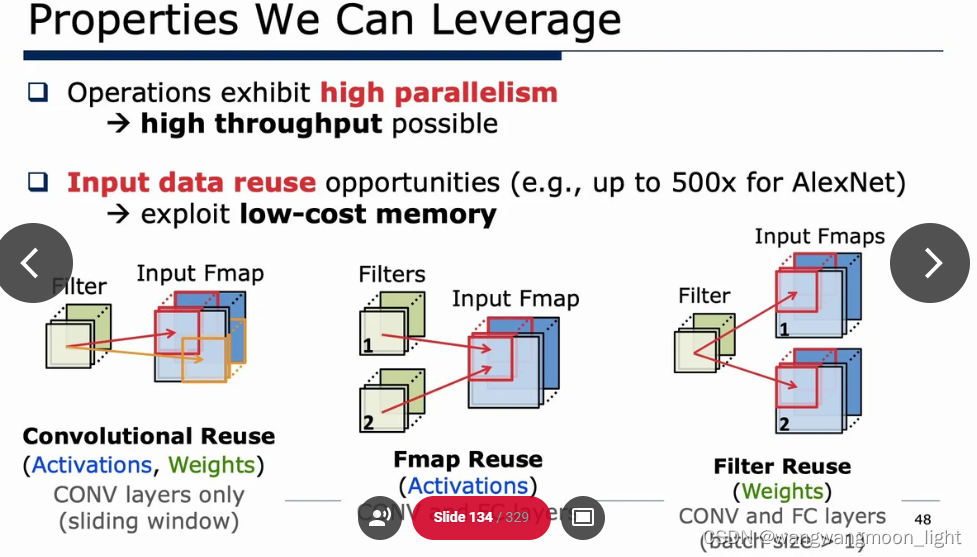
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

Properties We Can Leverage:

四份数据需要 RW, 所以下述倍数为4.
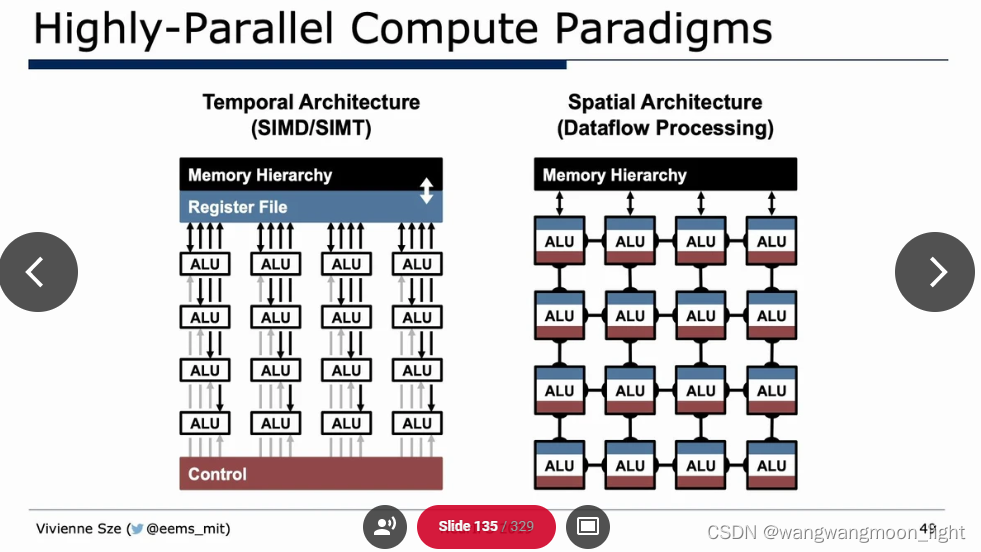
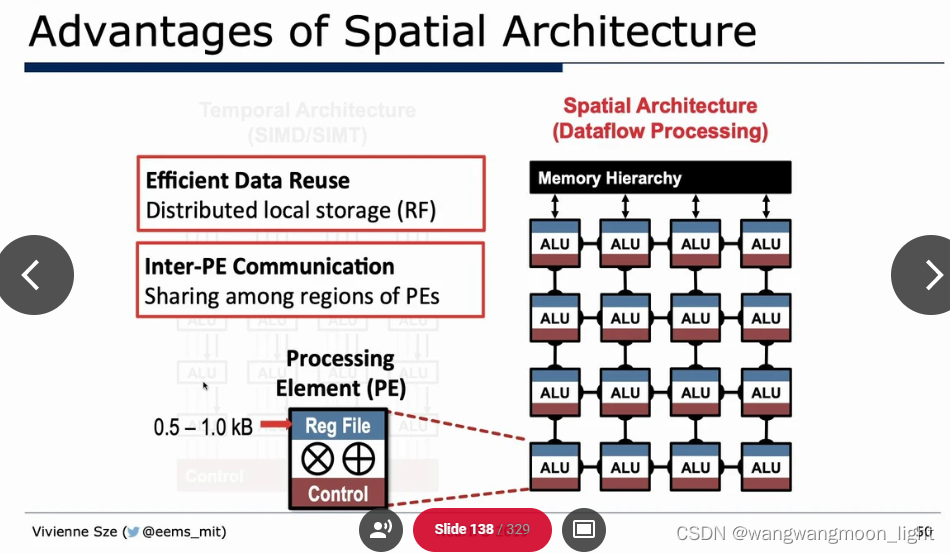
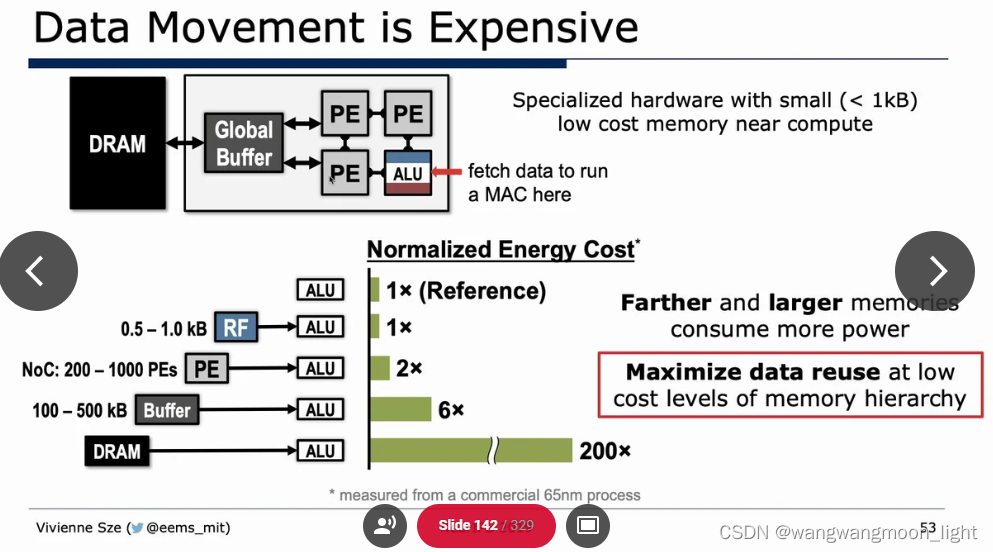
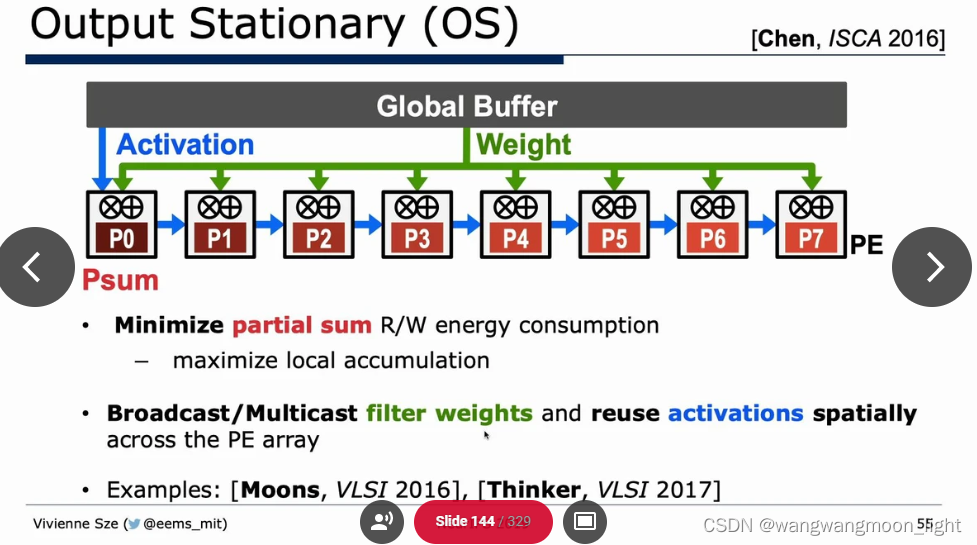
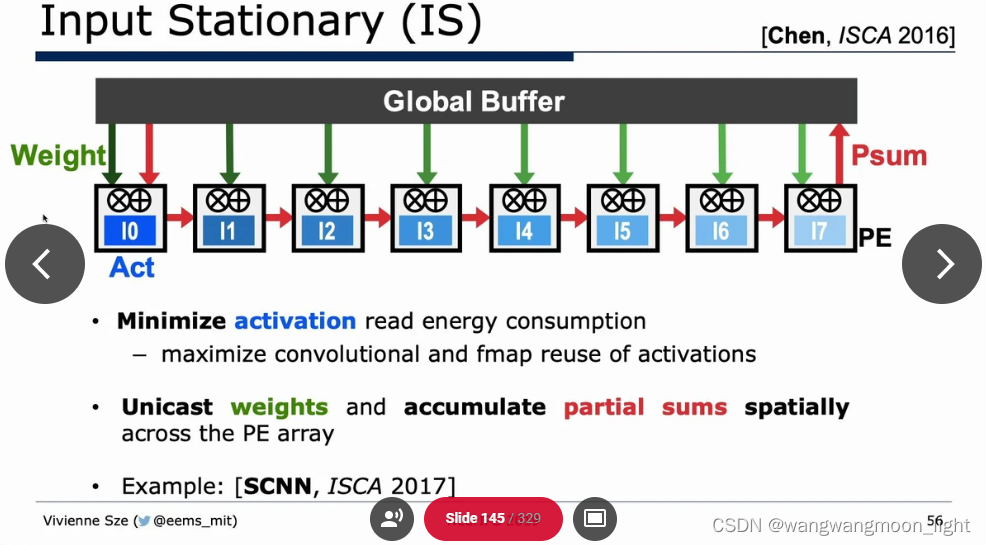
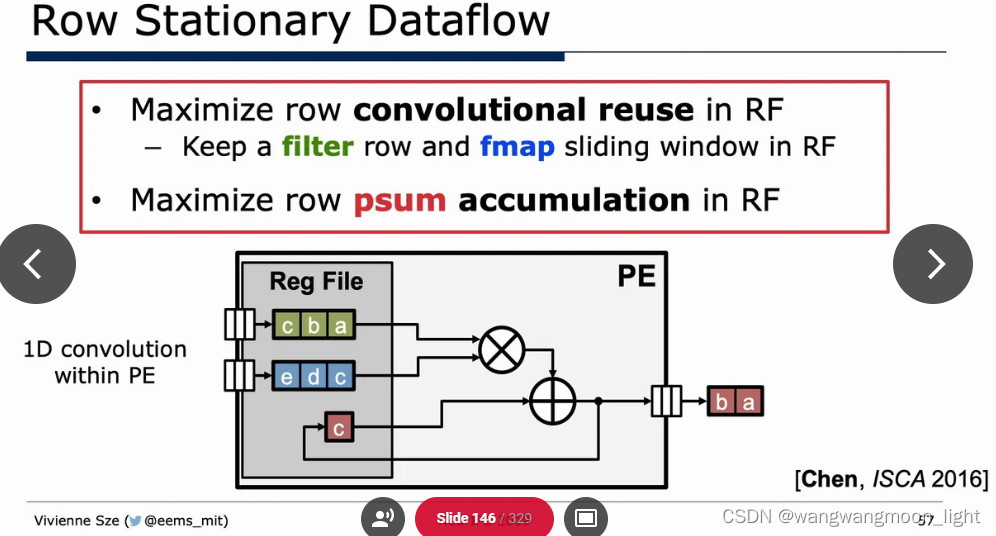
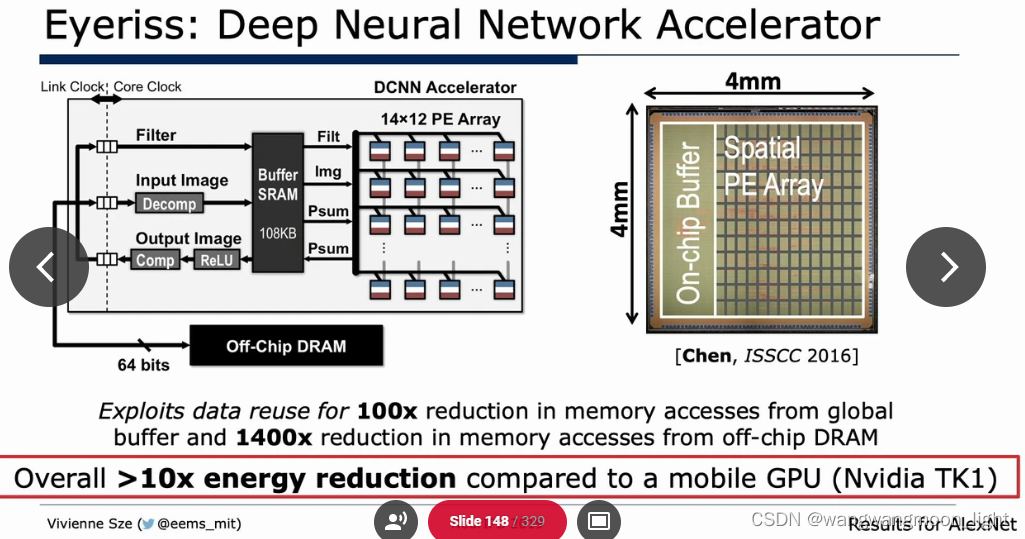
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

Algorithm & Hardware Co-Design:

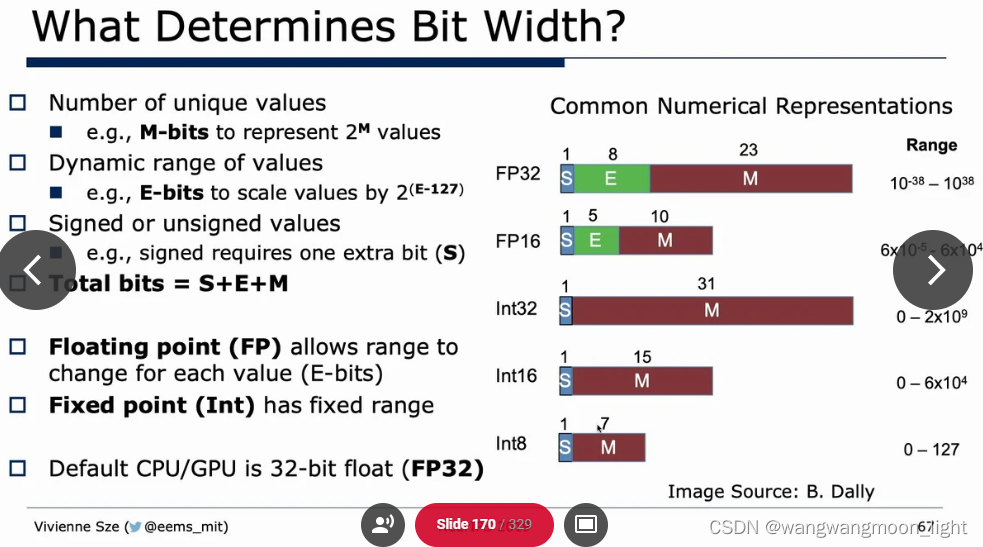
在这里插入图片描述

Reduce Precision:

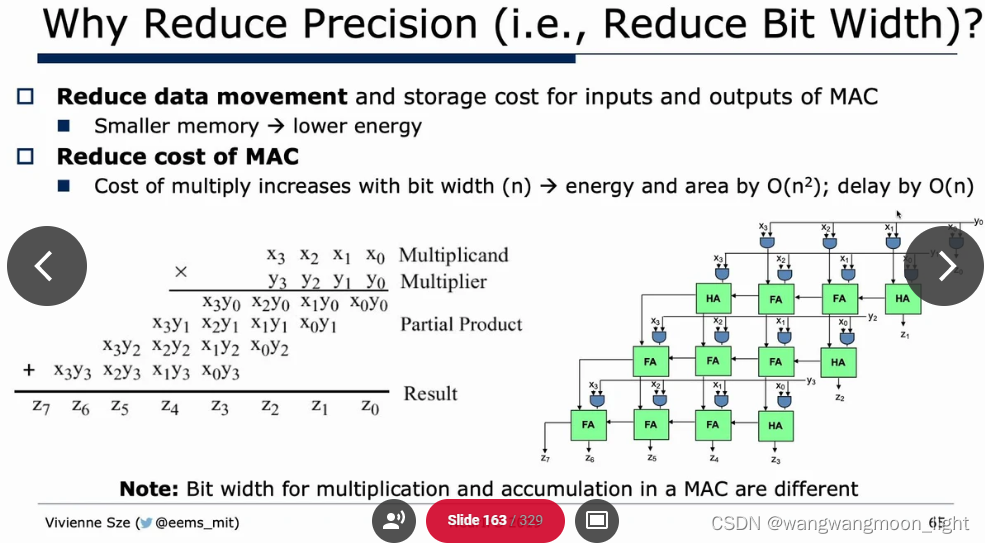
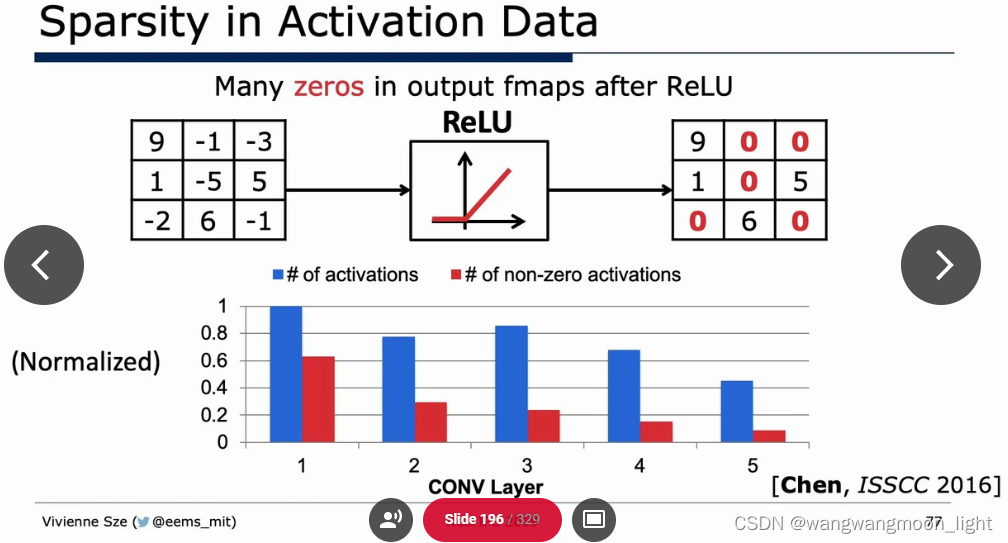
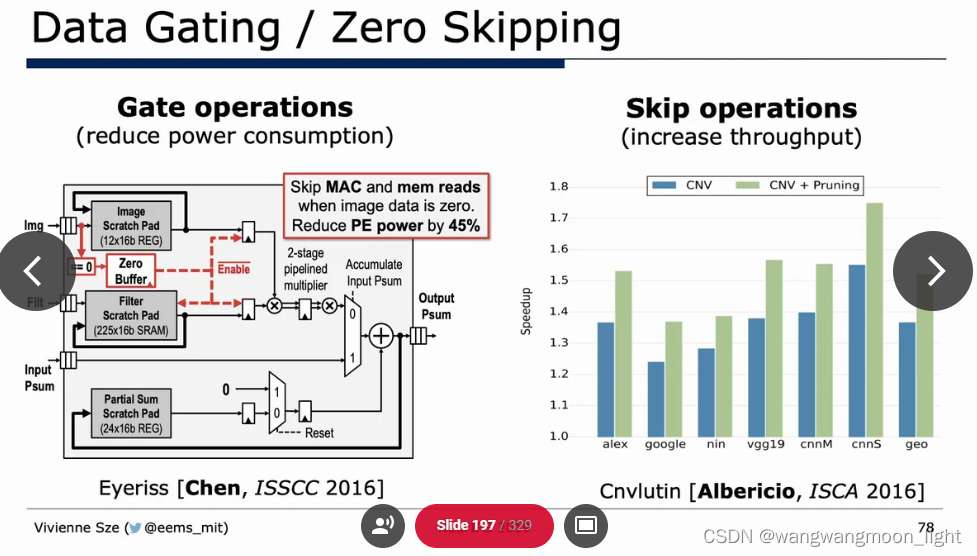
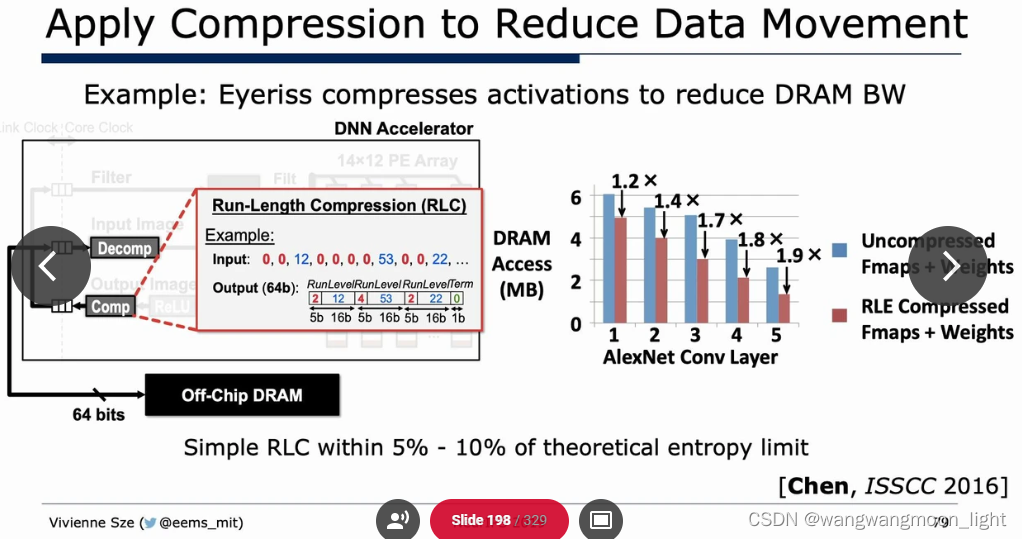
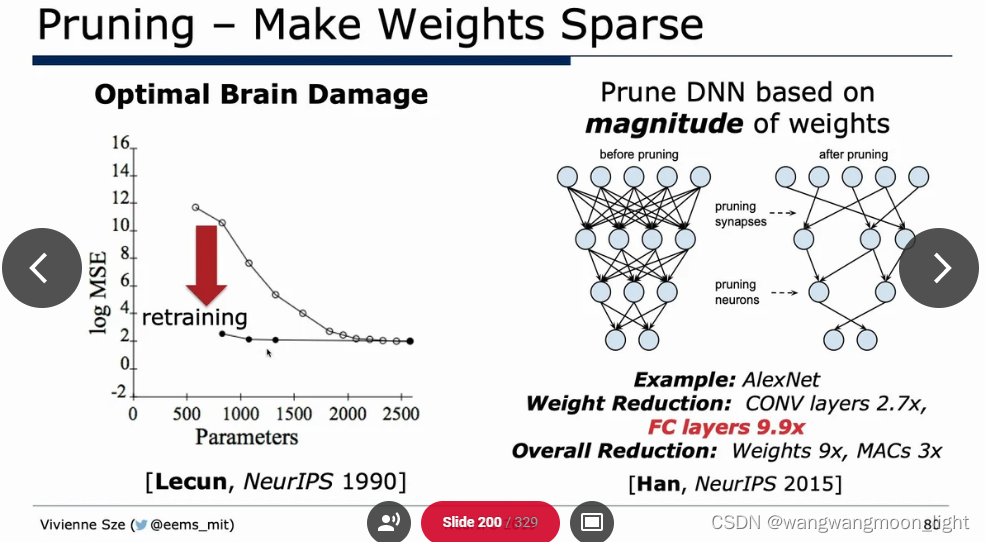
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

Sparsity:

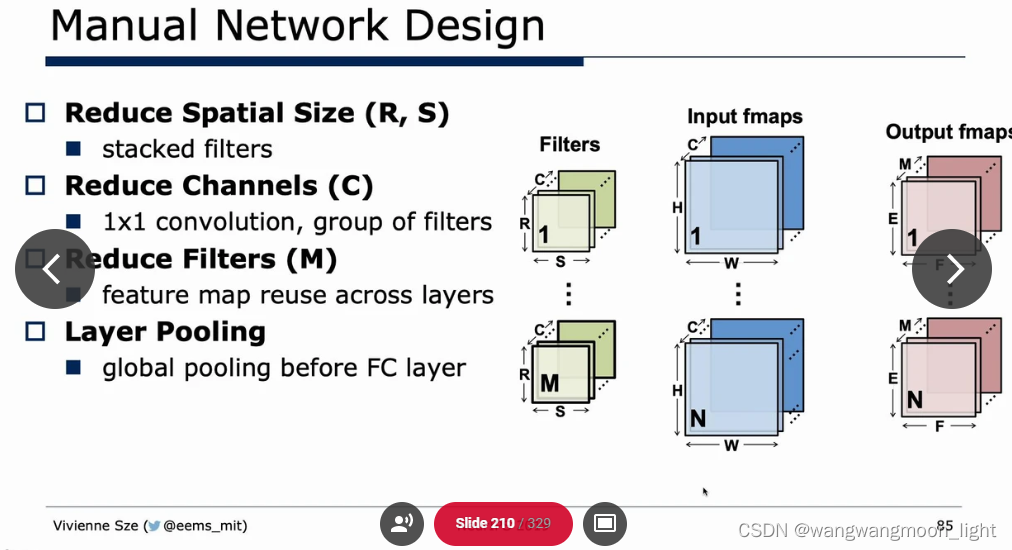
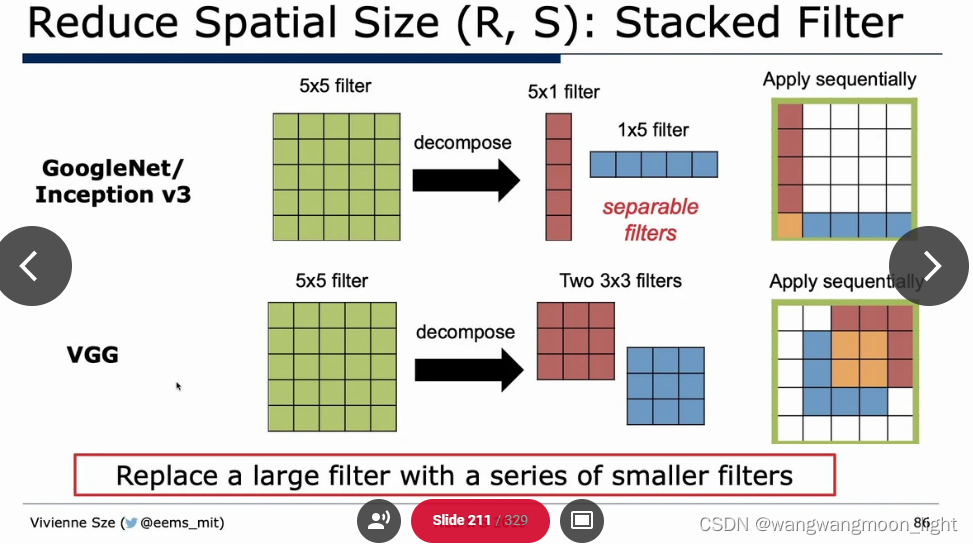
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

Efficient network architecture:

Sparsity: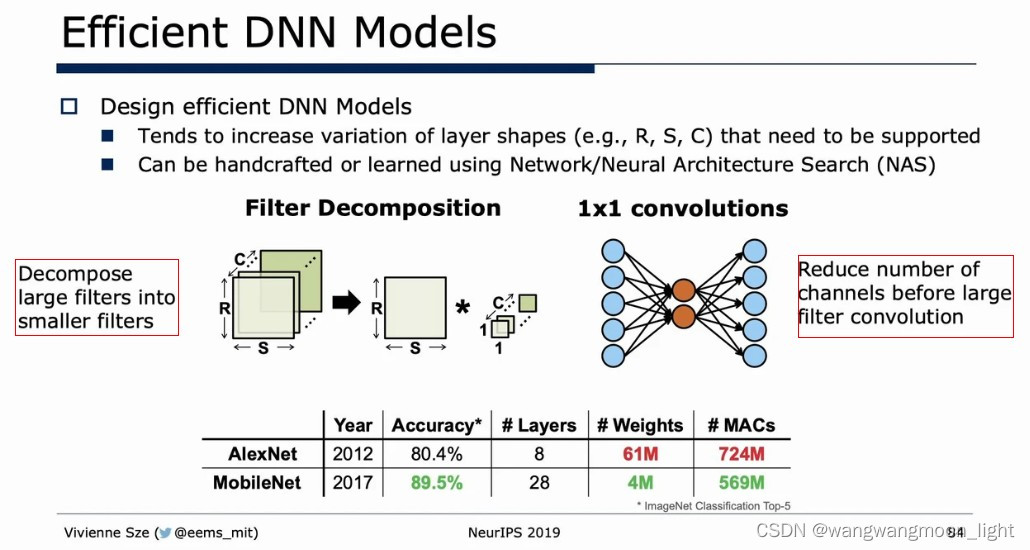请添加图片描述

在这里插入图片描述
在这里插入图片描述
Depthwise convolution:
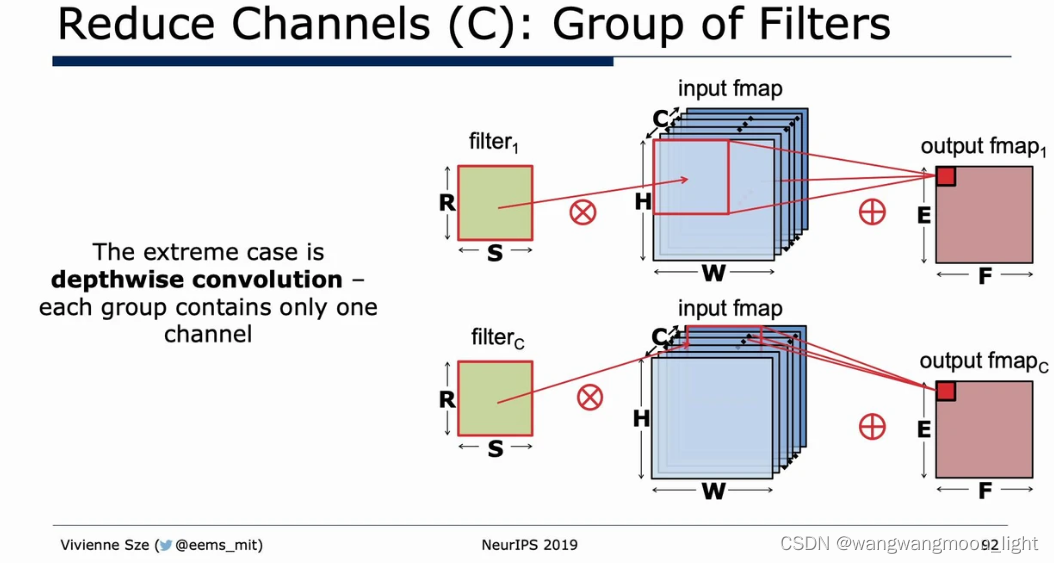
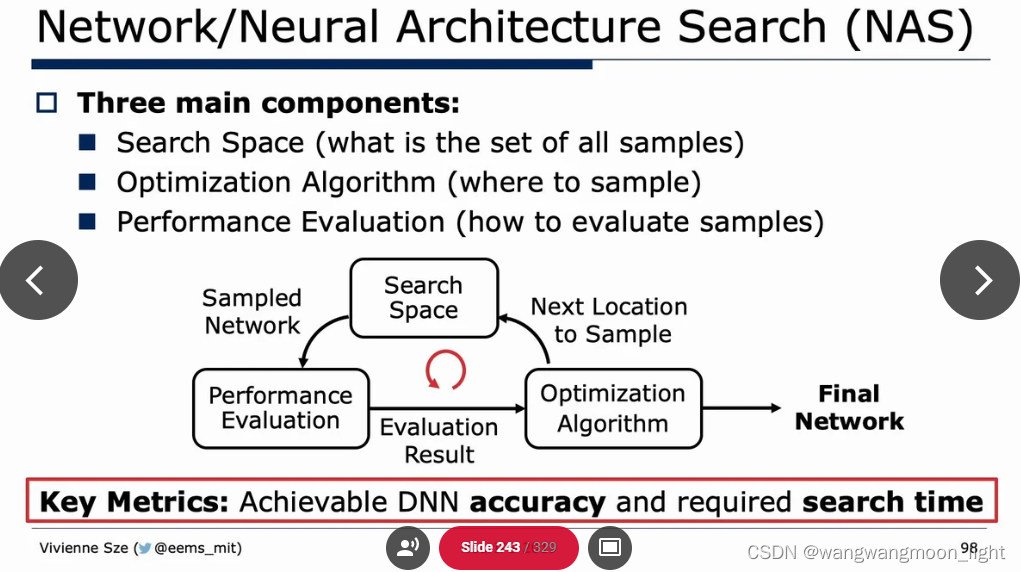
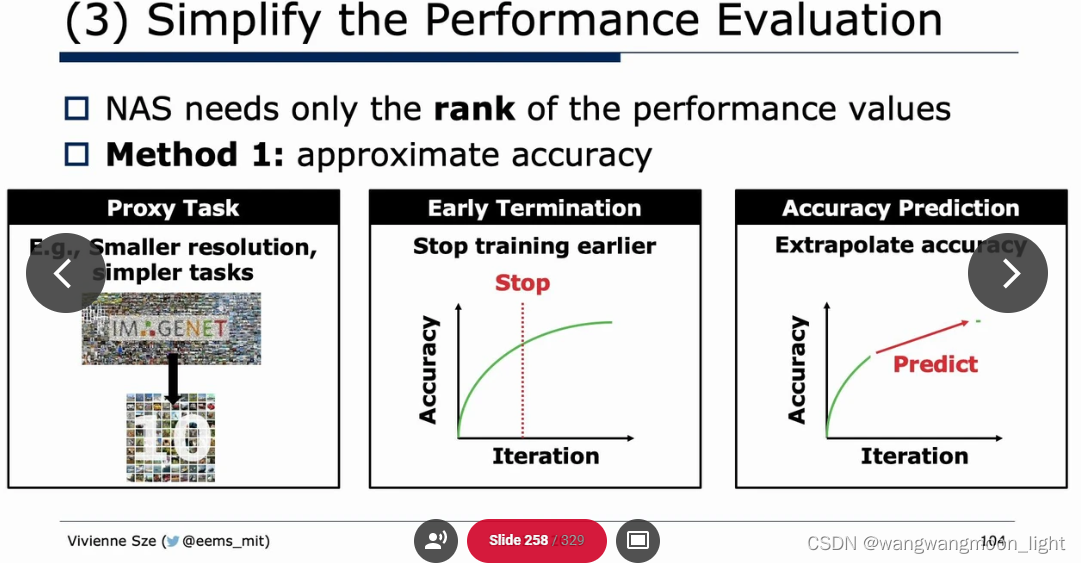
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

最低0.47元/天 解锁文章
Efficient Processing of Deep Neural Networks A Tutorial and Survey
03-16
该文档是顶会深度学习与硬件加速综述，对从本世纪初到现在的深度学习发展以及对应的硬件加速方法做了比较清晰的概述，非常具有代表性
深度学习国外综述论文 Efficient Processing of Deep Neural Networks: A Tutorial and Survey
09-05
非常全面的国外综述论文，对深度学习各个反向理论有一个全面的介绍！
Understanding Neural Networks Through Deep Visualization 论文笔记
Jayxbx的博客
05-02 1671
0 摘要 近年来，在训练大型深度神经网络方面取得了巨大进展，其中包括训练卷积神经网络识别自然图像。 然而，我们对这些模型如何工作的理解，特别是他们在中间层执行的计算，已经落后了。通过开发更好的可视化和解释神经网络的工具，这一领域的进展将进一步加速。 我们在这里介绍两种工具。 第一种是在处理图像或视频时，将训练过的每个图层上产生的激活可视化的工具。我们发现，随着用户输入的改变，通过查看实时的激活值...
AI算力加速：效率翻倍的入门学习指南
最新发布
zctzctzct123的博客
09-21 1032
第一部分：理解 AI 算力基础 - 效率的引擎第二部分：设计领域算力加速实战 - 告别漫长渲染第三部分：办公场景算力加速实战 - 智能自动化解放双手第四部分：创作领域算力加速实战 - 激发无限灵感第五部分：通用算力加速策略与未来展望
论文学习1----理解深度学习需要重新思考泛化Understanding deep learning requires rethinking generalization
I am what i am
06-14 2885
——论文地址：Understanding deep learning requires rethinking generalization1、有关新闻1.1 新闻一：参考1：机器之心尽管深度人工神经网络规模庞大，但它们的训练表现和测试表现之间可以表现出非常小的差异。传统的思考是将小的泛化误差要么归结为模型族的特性，要么就认为与训练过程中的正则化技术有关。通过广泛的系统性实验，我们表明这些传统的方法并
(MIT)Deep learning 学习笔记（1）
logicor的博客
03-20 846
从今天每天会定量学习DEEP LEARNING。MIT这本书可以说是DEEP LEARNING 方向的启蒙，这个博客系列将会是我学习笔记。 开篇就告诉了我们，这本书是为了想了解深度学习的年轻本科生或者像我这种想从图像算法转行做DL的人准备的。 人类的文化形成了近千年，人的意识早就抽象的不能早抽象了，虽然是由神经元的简单连接、刺激，但是人类的思维已经复杂到连人类自己都无法模拟了。国外曾经有人多次尝试通
Efficient processing of deep neural networks: A tutorial and survey
W0n9_的博客
01-15 1832
深度神经网络的高效处理：教程和综述 摘要 深度神经网络(DNN)目前广泛应用于计算机视觉、语音识别和机器人等人工智能(AI)领域。虽然DNN在许多AI任务上提供了最先进的精确度，但它以高计算复杂度为代价。因此，对于DNN在AI系统中的广泛部署而言，实现DNN的有效处理以提高能源效率和吞吐量而又不牺牲应用精度或增加硬件成本的技术至关重要。本文旨在提供一个有关实现DNN高效处理目标的最新进展的综合教程和综述。 具体来说，它将提供DNN的概述，讨论支持DNN的各种硬件平台和体系结构，并重点介绍仅通过硬件设计更改或
Meta-Learning in Neural Networks: A Survey元学习最新综述（翻译）
热门推荐
qq_38680752的博客
06-02 1万+
近年来，元学习领域，即“为学习而学习”，已经引起了人们极大的兴趣。与传统的人工智能方法不同，传统的人工智能方法是使用固定的学习算法从头开始解决给定的任务，元学习的目的是改进学习算法本身，考虑到多次学习的经验。这个范例提供了一个机会来解决深度学习的许多传统挑战，包括数据和计算瓶颈，以及泛化的基本问题。在这项调查中，我们描述了当代元学习的景观。我们首先讨论元学习的定义，并将其定位于相关领域，如转移学习、多任务学习和超参数优化。然后我们提出了一种新的分类方法，它提供了当今元学习方法的更全面的细分。我们综述了元学习
Deep learning_CNN_Review：A Survey of the Recent Architectures of Deep Convolutional Neural Networks—...
Alliswell_WP
11-08 2744
CNN综述文章的翻译 [2019 CVPR] A Survey of the Recent Architectures of Deep Convolutional Neural Networks 翻译 综述深度卷积神经网络架构：从基本组件到结构创新 目录 摘要 1、引言 2、CNN基本组件 2.1 卷积层 2.2 池化层 2...
大数据AI人工智能与 GPU、TPU 超级算力融合引领人类智能时代技术革命原理与应用实践
AI天才研究院
09-01 2157
在21世纪的第三个十年,我们正站在人类智能时代的门槛上。这个新时代的到来,得益于大数据、人工智能(AI)以及GPU(图形处理器)和TPU(张量处理器)等超级算力的融合与发展。这些技术的结合不仅推动了科技的进步,更是引领着一场深刻的技术革命,正在重塑我们的社会、经济和生活方式。大数据为AI提供了海量的训练素材,使得机器学习模型能够从中提取出有价值的模式和知识。而AI算法的不断优化和创新,则让我们能够更有效地利用这些数据,实现更智能、更精准的决策和预测。
Graph Neural Networks: A Review of Methods and Applications（图神经网络：方法与应用综述）
weixin_41697507的博客
07-06 5886
Graph Neural Networks: A Review of Methods and Applications Jie Zhou , Ganqu Cui , Zhengyan Zhang , Cheng Yang, Zhiyuan Liu, Lifeng Wang, Changcheng Li, Maosong Sun Abstract—Lots of learning tasks req...
AI算力平台如何支持深度学习模型的部署（非常详细）从零基础到精通，收藏这篇就够了！
Python_0011的博客
06-21 625
包括算法开发、模型训练和推理部署等。
MIT深度神经网络硬件架构设计教程
09-03
MIT EYERISS芯片设计指导教程，基于FPGA/ASIC神经网络设计的干货
Efficient Processing of Deep Neural Networks: A Tutorial and Survey
05-08
This article aims to provide a comprehensive tutorial and survey about the recent advances towards the goal of enabling efficient processing of DNNs. Specifically, it will provide an overview of DNNs, discuss various hardware platforms and architectures that support DNNs, and highlight key trends in reducing the computation cost of DNNs either solely via hardware design changes or via joint hardware design and DNN algorithm changes.
论文阅读笔记（五十三）：Understanding Deep Convolutional Networks
sunshine_010的博客
05-14 1279
Abstract Deep convolutional networks provide state of the art classifications and regressions results over many high-dimensional problems. We review their architecture, which scatters data with a cas...
【人工智能】“AI + 算力 = 最强龙头”，你怎么看？
wzk4869的博客
06-19 5339
【人工智能】“AI + 算力 = 最强龙头”，你怎么看？
Efficient parametrization of multi-domain deep neural networks
sinat_30618203的博客
08-12 972
常见的迁移学习任务 1、multi-task model 同时适用于多个task 2、multi-domain model 同时适用于多个domain 3、extensible model 模型可随时间进化，通过之前学习的知识来迁移到新的任务和domain上 创新 定义网络为；w是universal v...
论文阅读记录(Efficient Processing of Deep Neural Networks: A Tutorial and Survey)(毕设笔记5)
fenggang2333的博客
02-03 830
论文阅读(Efficient Processing of Deep Neural Networks: A Tutorial and Survey)(毕设笔记5) section 1: 导言 section 2: 介绍DNN的历史和应用，说明DNN的重要性 section 3: 概述了DNN的基本组成部分，介绍了一些流行的DNN模型 section 4: 介绍了用于DNN研究和开发的各种资源 section 5: 介绍了处理DNN的硬件平台，和各种用于提高吞吐量和能效的优化 section 6: 讨论了混合信
神经网络和深度学习-第4周 deep-neural-network
you1314520me的专栏
05-28 1626
NoteThis is my personal note at the 4th week after studying the course neural-networks-deep-learning and the copyright belongs to deeplearning.ai.01_deep-neural-networkWelcome to the fourth week of th...
tensorflow-deep-neural-networks-master
08-29
tensorflow-deep-neural-networks-master是一个基于TensorFlow的深度神经网络的代码库。TensorFlow是一个开源的机器学习框架，它提供了一套丰富的工具和库，用于构建和训练各种类型的神经网络模型。这个代码库中的...
评论 1
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值