1.8 LeetCode总结（树）_二叉树类

原创

已于 2025-10-12 22:49:47 修改 · 817 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #职场和发展

于 2020-03-02 22:51:25 首次发布

本文深入探讨二叉树的多种遍历方法，包括前序、中序、后序及层序遍历，并解析二叉树的翻转、对称性判断、深度计算等核心算法。同时，讲解了如何解决诸如平衡二叉树、二叉树坡度、合并二叉树等进阶问题，以及二叉树展开为链表和二叉搜索树的第k大节点等挑战性任务。

编程总结

每每刷完一道题后，其思想和精妙之处没有地方记录，本篇博客用以记录刷题过程中的遇到的算法和技巧

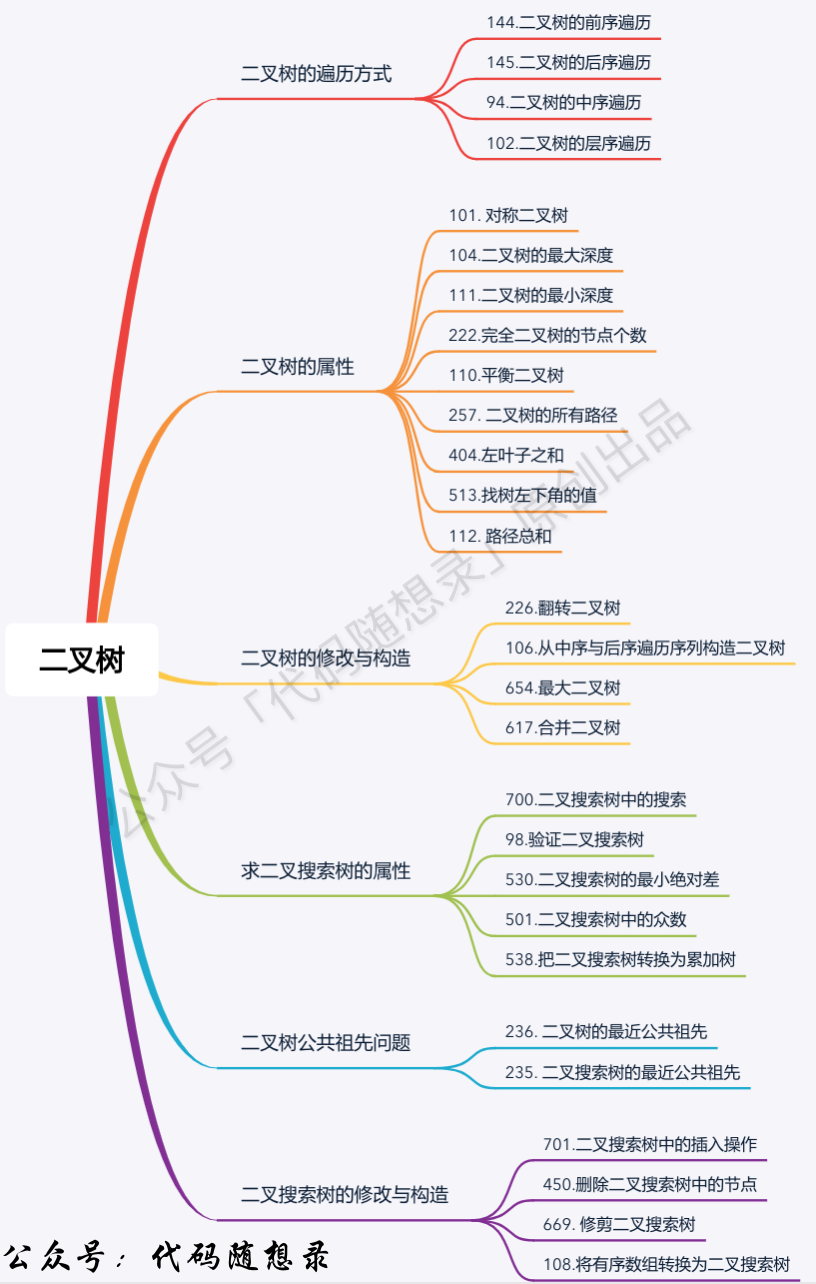
在这里插入图片描述

二叉树的遍历方式

前中后序遍历–递归法_一刷(80%)

确定递归函数的参数和返回值

确定终止条件

确定单层递归的逻辑

// 前序 根左右
void PreOrder(struct TreeNode *root, int *ret, int *retIndex)
{
   
   
    if (root == NULL) {
   
   
        return;
    }
    ret[(*retIndex)++] = root->val; // 根计算
    PreOrder(root->left, ret, retIndex); // 左
    PreOrder(root->right, ret, retIndex); // 右
}
// 中序 左根右
void inorder(struct TreeNode *root, int *res, int *resSize) 
{
   
   
    if (root == NULL) {
   
   
        return;
    }
    inorder(root->left, res, resSize); // 左
    res[(*resSize)++] = root->val; // 根
    inorder(root->right, res, resSize); // 右
}
// 后序  左右根
void postorder(struct TreeNode *root, int *res, int *resSize)
{
   
   
    if (root == NULL) {
   
   
        return;
    }
    postorder(root->left, res, resSize);
    postorder(root->right, res, resSize);
    res[(*resSize)++] = root->val;
}
// 调用函数
int *preorderTraversal(struct TreeNode *root, int *returnSize)
{
   
   
    int retIndex = 0;
    int *ret = (int *)malloc(sizeof(int) * 100);
    memset(ret, 0, sizeof(int) * 100);
    PreOrder(root, ret, &retIndex);
    *returnSize = retIndex;
    return ret;
}

102. 二叉树的层序遍历 – BFS__一刷(80%)

在这里插入图片描述

注意结果res的手法处理，同样重要

思路：BFS

int **levelOrder(struct TreeNode *root, int *returnSize, int **returnColumnSizes)
{
   
   
    if (root == NULL) {
   
   
        *returnSize = 0; // 代码入口如果是空的话，应该给设定返回值为0,不能只简单的返回NULL就结束
        return NULL;
    }
    struct TreeNode *queue[2001];
    int tail = 0, head = 0, len = 0;
    int idx = 0;
    int **res = (int **)malloc(sizeof(int *) * 2001);
    *returnColumnSizes = (int *)malloc(sizeof(int) * 2001);
    queue[tail++] = root; // 1. 根节点入队列
    *returnSize = 0;
    while ((tail - head) > 0) {
   
    // 队列不为空
        len = tail - head;
        idx = 0;
        res[*returnSize] = (int *)malloc(sizeof(int) * len);
        for (int i = 0; i < len; i++) {
   
   
            struct TreeNode *tmp = queue[head++]; // 出队列
            res[*returnSize][idx++] = tmp->val;
            if (tmp->left != NULL) {
   
   
                queue[tail++] = tmp->left;
            }
            if (tmp->right != NULL) {
   
   
                queue[tail++] = tmp->right;
            }
        }
        (*returnColumnSizes)[*returnSize] = len;
        *returnSize = *returnSize + 1;
    }
    return res;
}
int main()
{
   
   
    struct TreeNode root, left, right;
    struct TreeNode r_left, r_right;
    left    = (struct TreeNode) {
   
    9,  NULL, NULL };
    r_right = (struct TreeNode) {
   
    7,  NULL, NULL};
    r_left  = (struct TreeNode) {
   
    15, NULL, NULL };
    right   = (struct TreeNode) {
   
    20, &r_left, &r_right };
    root    = (struct TreeNode) {
   
    3,  &left,   &right };
    int returnSize;
    int *returnColumnSizes;
    int **ret = levelOrder(&root, &returnSize, &returnColumnSizes);
    for (int i = 0; i < returnSize; i++) {
   
   
        for (int j = 0; j < returnColumnSizes[i]; j++) {
   
   
            printf("%d ", ret[i][j]);
        }
        printf("\n");
    }
    return 0;
}

226. 翻转二叉树_一刷(80%)

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。
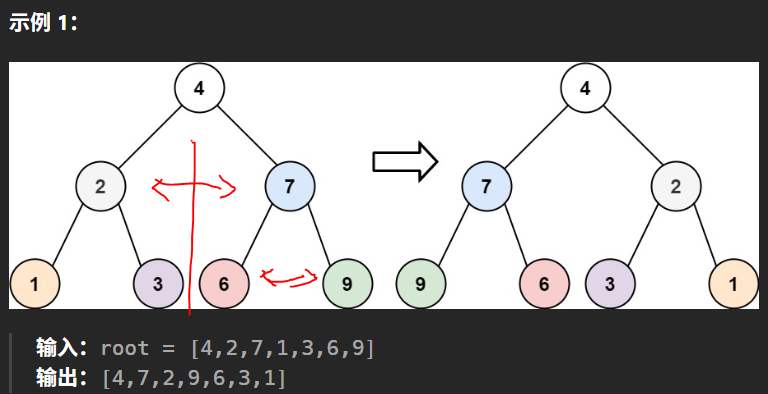
在这里插入图片描述

90% of our engineers use the softwar you wrote(Homebrew), but you can’t invert a binary tree on a whiteboard so fuck off.

思路：前序遍历，两两交换节点

1）确认返回是 TreeNode
2）确定终止条件
3）交换两两节点
前序遍历：

struct TreeNode *invertTree(struct TreeNode *root)
{
   
   
    if (root == NULL) {
   
     // 1.递归终止条件
        return NULL;
    }
    // 前序遍历，根左右
    // 交换 root 的左右孩子
    struct TreeNode *left  = root->left;
    struct TreeNode *right = root->right;
    root->left = right; // 先递下去，归的时候遇到节点时，交换其左右节点
    root->right = left; // 本质时交换每个除根节点外节点的左右子节点
    invertTree(root->left);
    invertTree(root->right);
    return root;
}
int main()
{
   
   
    struct TreeNode root, left, right;
    struct TreeNode r_left, r_right;
    struct TreeNode l_left, l_right;
    r_right = (struct TreeNode) {
   
    6,  NULL, NULL};
    r_left  = (struct TreeNode) {
   
    9,  NULL, NULL };
    l_right = (struct TreeNode) {
   
    3,  NULL, NULL };
    l_left  = (struct TreeNode) {
   
    1,  NULL, NULL };
    left    = (struct TreeNode) {
   
    2,  &l_left, &l_right };
    right   = (struct TreeNode) {
   
    7,  &r_left