【读论文04】-生长型滑坡预测- BG-CNN-LSTM

【读论文04】–滑坡位移预测-Biological growth models and CNN-LSTM

先用生物生长模型（BG）提取滑坡位移时序的蠕变特征（位移、速度、加速度等），再将这些特征作为输入，结合外部环境因素（如降雨、库水位），输入到CNN-LSTM模型中进行动态预测。

摘要

存在问题：受复杂外部因素影响，储集层滑坡的位移-时间曲线表现出短期和长期的多样性和动力复杂性。现有的方法，包括回归模型和神经网络模型，由于没有考虑滑坡蠕变特征，很难进行多特征耦合位移预测。
解决方法：本文将滑坡蠕变特性与非线性智能算法相结合，提出了一种基于生物生长模型（BG）、卷积神经网络（CNN）和长短期记忆网络（LSTM）相结合的动态智能滑坡位移预测方法。
具体措施：这种预测方法改进了三种不同的生物生长模型，从而有效地提取了滑坡蠕变特征参数。同时，它整合了外部因素 （降雨量和水库水位） 构建了用于数据增强的内部和外部综合数据集，并将其输入到改进的 CNN-LSTM 模型中。此后，利用 CNN 的鲁棒特征提取能力和空间平移不变性，该模型自主捕获滑坡位移的短期局部波动特征，并结合 LSTM 对长期非线性时间数据的高效处理来提高预测性能。
效果：对三峡库区凉水井滑坡的评价表明，BG-CNN-LSTM在处理各类滑坡时表现出较高的预测精度和优异的泛化能力。该研究为实现多特征耦合滑坡的全过程、实时、高精度位移预测提供了一种创新方法。

引言

引出问题
三峡库区地质条件复杂，滑坡灾害频发，常造成人员伤亡和财产损失。这些滑坡的累积位移曲线呈现多样化特征，并随时间动态演变。因此，开发一种能够准确预测长期动态变化、同时捕捉短期局部形变的滑坡预测模型，对灾害防治和风险管理至关重要。
存在缺陷
传统滑坡预测方法主要基于蠕变理论的三阶段模型，虽然在滑坡加速变形阶段预测效果较好，但对初期和稳定阶段的长期变形预测能力不足。这一局限性制约了滑坡灾害的精准预警和防控效果。
引出研究内容
滑坡变形演化过程除与蠕变过程相似外，还具有类似生物生长、发育和成熟的规律特征。因此，生物生长模型也可用于滑坡变形预测，常用的包括Pearl模型、Gompertz模型、Verhulst模型和Weibull模型等。这些模型在滑坡预测和地面沉降预报等领域已有应用，但主要适用于短期预测，难以处理非线性问题，适用范围有限。本文利用生物生长模型进行曲线拟合的优势，提取滑坡蠕变的特征参数。
目前研究存在缺点
近年来，研究者们开发了多种考虑库水位波动、降雨等外部因素的智能滑坡预测模型。回归模型（如逻辑回归、广义回归神经网络和灰色预测模型）已被广泛应用，但这些线性模型难以捕捉滑坡位移的非线性变化特征。神经网络模型（包括支持向量机、长短期记忆网络和极限学习机）虽然有所改进，但单一的机器学习方法仍难以自主学习和提取滑坡变形的局部波动规律。混合模型（如CNN-BiGRU和CEEMDAN-GRU组合）能更好地反映滑坡非线性特征，但在参数蠕变特性捕捉、滑坡运动行为与外部因素协同预测，以及对持续演变的不同类型滑坡实现高精度预测等方面仍存在挑战。

（说明：
1. 采用"总-分"结构，先概述研究背景，再分类阐述模型特点与局限
2. 使用"虽然…但…“等转折句式突出技术瓶颈
3. 专业术语保留英文缩写并标注中文全称
4. 通过"协同预测”"持续演变"等术语体现学术性
5. 最终落脚于当前模型的核心挑战，为后续研究创新做铺垫）

本文方法
综合来看，蠕变理论、生物生长模型和非线性智能模型均具备滑坡位移预测能力，但普遍存在适用性受限和动态预测精度不足等局限。蠕变理论能准确刻画滑坡变形特征，生物生长模型擅长从运动学角度阐释滑坡变形趋势并提取蠕变特征参数，非线性智能模型则可系统考虑滑坡位移的多元影响因素。
本研究提出了一种基于生物生长模型与CNN-LSTM的滑坡位移动态预测新方法：首先利用生物生长模型提取滑坡蠕变特征，构建融合内外因的综合增强数据集；继而通过CNN模型强大的特征提取能力、参数共享和空间平移不变性优势，有效捕捉滑坡变形的局部特征并灵活处理动态位移数据；同时借助LSTM模型精准关联多因素对滑坡变形的影响，其任意非线性动态系统逼近能力则助力实现滑坡动态非线性预测。最终将该创新模型应用于凉水井滑坡位移预测，并进行误差与精度分析。

（技术亮点说明：
1. 采用"总-分-总"结构，先归纳现有方法优劣，再分层阐述新方法技术路线
2. 使用"特征提取"“参数共享”“动态逼近"等专业术语保持学术严谨性
3. 通过"融合内外因”"综合增强数据集"等表述突出方法创新性
4. 运用分号结构清晰展示CNN与LSTM的协同机制
5. 结尾强调实证应用与验证环节，体现研究完整性）

2 方法论

基于生物生长模型和CNN-LSTM的滑坡位移动态智能预测方法包含两大核心模块：首先是对三种典型生物生长曲线模型的改进及滑坡蠕变特征分析；其次是构建新型CNN-LSTM融合模型进行滑坡位移预测。

2.1 生物生长模型

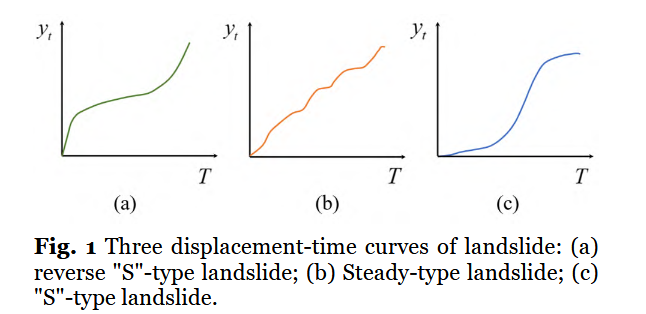
由于滑坡位移监测数据随时间演变呈现非线性趋势，其累积位移曲线可视为非线性时间序列曲线。受多种外部因素和数据采集时序影响，监测系统记录的累积位移曲线可能表现出多样化特征（Miao等，2018）。本文重点研究三类典型累积位移曲线：反"S"型滑坡、稳态型滑坡和"S"型滑坡，如图1所示。

2.1.1 Verhulst反函数及其改进方法

针对部分滑坡位移-时间曲线与Verhulst反函数曲线高度吻合的特点（完整呈现滑坡三阶段蠕变特征），本研究采用Verhulst反函数模型拟合反"S"型滑坡位移监测数据（图1a），以分析滑坡蠕变特征并预测其发展趋势。
某些滑坡的位移-时间曲线与Verhulst逆函数曲线相似，表现出完整的三个阶段蠕变特征（初始、稳定、加速阶段）。原始VIF模型的通用表达式为：
$$y=\frac{\alpha \mu }{1+e^{-v\left(x-x_0\right)}}+\lambda$$
其中，$(x_0,\mu ,v,\lambda )$为待定参数。
模型改进：
• 为提高VIF模型与“反S型”滑坡变形曲线的匹配性，提出改进公式：
$$S(t)=c\times \ln \frac{at+b}{b-t}$$
参数$a,b,c$需通过拟合确定。改进后的模型特点：
◦ 当滑坡变形趋近无穷时，时间(t)趋近于(b)，即累积位移趋势线为(t=b)。
◦ 通过一阶和二阶导数可进一步得到滑坡的蠕变速率$V^{\prime }(t$)和加速度$a^{\prime }(t)$。

2.1 . 2 Gompertz函数及其改进

Gompertz 曲线常用于描述生物生长趋势，其基本表达式为：
$$y=e^{(k+a{b}^t)}$$
其中，(a, b, k) 为待定参数。
模型改进
• 为使 Gompertz 模型更适用于稳定型滑坡（位移随时间趋于稳定），提出改进公式：
$$S(t)=K{e}^{-a{e}^{-bt}}$$
其中，(a, b, K) 为待定参数。改进后的模型特点：
• 当时间 $(t\to \infty )$，累积位移 $(S(t))$ 趋近于$(K)$，即趋势线为 $(S(t)=K)$。
• 通过求导可进一步分析滑坡的蠕变速率和加速度特征。

2.1.3 Weibull函数及其改进

该小节介绍了Weibull 生长模型及其改进方法，用于拟合S型滑坡（S-type landslide）的位移监测数据，主要内容如下： Weibull 曲线是一种灵活的生长模型，其基本表达式为：
$$y=a-(a-b)e^{-(kx{)}^c}$$
其中，(a, b, c, k) 为待定参数，且：
• 当 (a > b) 时，(c > 0)（适用于增长型曲线）；
• 当 (a < b) 时，(c < 0)（适用于衰减型曲线）。
模型改进
• 为使 Weibull 模型更适用于S型滑坡（位移初期增长缓慢，中期加速，后期趋于稳定），提出改进公式：
$$S(t)=a-(a-b)e^{-(kt{)}^c}$$
其中，(a, b, c, k) 为待定参数。改进后的模型特点：
• 初始时刻（(t = 0)）：位移 (S(t) = b)，反映滑坡初始变形状态。
• 长期趋势$（(t\to \infty )）$：位移 (S(t)) 趋近于 (a)，即趋势线为 (S(t) = a)。
• 通过求导可进一步分析滑坡的蠕变速率和加速度特征。

2.2 CNN - LSTM滑坡位移预测模型

2.2.1 CNN（卷积神经网络）

1. 卷积层的作用

• 特征提取：通过卷积运算（数学表达式如下）从输入数据中提取局部特征和高维空间的相关性：
$$F\otimes w=\sum _{k=1}^M\sum _{j=1}^{W_j}\sum _{i=1}^{H_i}\left(F^k(i,j)w^k(i,j)\right)$$
其中，(F) 为输入数据，(w) 为卷积核权重，(M)、(H_i)、(W_j) 分别表示卷积核的通道数、高度和宽度。
• 参数共享与平移不变性：卷积核在输入数据上滑动计算，减少参数量并保持对局部特征的稳定识别能力。

2. 池化层的作用

• 特征降维：通过最大池化（Max Pooling）等操作压缩数据维度，保留关键特征并减少计算复杂度。
• 特征不变性：增强模型对输入数据微小变化的鲁棒性（如位移监测数据的波动）。

2.2.2 LSTM（长短期记忆网络）

• LSTM是RNN（循环神经网络）的改进变体，专门用于处理时序数据的长期依赖问题。
• 相较于传统RNN，LSTM通过引入门控机制（遗忘门、输入门、输出门）有效缓解了梯度消失/爆炸问题。

2.2.3 CNN-LSTM

在图2中显示的增强的CNN-LSTM模型框架主要由数据输入层，CNN卷积层，池层，LSTM层和结果输出层组成。该模型的内部体系结构的结构如下：首先，综合数据集经过标准化并被送入CNN卷积层。这些层采用多种卷积，同时采用宽核来适应提取特征。此后，提取的特征通过最大良好层进行维数，从而确保了基本特征的保存。随后，这些减少尺寸的特征将输入到LSTM层中，以促进顺序特征的训练和获取。该模型采用ADAM算法进行反向传播，迭代更新模型参数。最后，执行数据输出以实现精确的滑坡位移预测。

2.3 BG-CNN-LSTM滑坡位移预测模型

首先，组织滑坡位移监测数据;Gompertz 模型、Weibull 模型和 VIF 模型用于拟合不同类型滑坡的曲线。确定了每个模型的最佳参数，从而获得了滑坡蠕变的特征参数，包括位移和速度。这三种不同的生物生长模型为识别边坡变形阶段和预测滑坡位移提供了基础模型。值得注意的是，预测未来蠕变特征的参数是通过用三个模型训练历史数据获得的，提供预测性见解，同时作为数据增强的过程。

接下来，使用内部和外部因素作为输入变量构建智能动态 CNN-LSTM 模型。内部因素指标包括从上述三个模型（位移、速度和加速度）获得的滑坡蠕变特征参数，而外部因素指标包括相应的水库水位和降雨监测数据。这些变量用于训练集成的 BG-CNN-LSTM 模型以匹配目标变量。这个综合模型在准确预测不同类型滑坡的位移方面具有重要的应用价值，尤其是那些具有动态变化的滑坡。

最后，为了评估预测模型的性能，本研究引入了平均绝对误差 （MAE）、平均绝对百分比误差 （MAPE） 和均方根误差 （RMSE）。MAE 表示预测值与实际值之间绝对差值的平均值。MAPE 表示预测值和实际值之间的百分比差异，然后取这些百分比差异的平均值。它通常以百分比表示。RMSE 表示观测值和预测值之间差值的二阶矩的平方根。在考虑误差方向时，MAE、MAPE 和 RMSE 的值较低表示模型的预测性能越准确、越好。

3 案例研究：凉水井滑坡

3.1 研究区域

3.1.1 地质条件

凉水井滑坡是三峡库区具有代表性的典型大型滑坡,其基本特征如下：

参数	数值	备注
长度	434 m	前缘至后缘水平距离
宽度	348 m	横向展布范围
平均厚度	34.5 m	滑体体积计算关键参数
面积	11.82×10⁴ m²	约17.7个标准足球场面积
体积	407.79×10⁴ m³	属特大型滑坡
前缘高程	100 m	常年处于库水位以下
后缘高程	319.5 m	最大高差达220 m
平均坡度	24°	原始坡面角度30°-35°
滑动方向	N偏北向	与长江流向呈锐角相交

3.1.2 监控系统

滑坡区域共安装了 26 个 GPS 位移监测点、9 个 GNSS 位移监测点、6 个地裂缝监测点，以及降水和水库水位测量设备。

3.2 变形特征

三峡水库试验蓄水后，凉水井滑坡由于水位上升而经历了不同程度的地表变形。在低水位和强降雨期间，滑坡变形加剧。主要表现为滑坡后部表面张力裂缝完全贯穿、滑坡中部侧向表面张力裂缝、中前部剪切裂缝、两侧倾斜裂缝。

3.2.1 累积地表位移

1. 水库水位影响
   • 高水位期（10月~1月）：水位约175m，位移增长平缓
   • 水位下降期（1月~5月）：位移增长率显著提高
   • 低水位期（5月~6月）：水位约145m，位移增速减缓
   • 水位上升期（6月~10月）：位移增长较稳定

2. 降雨影响
   • 雨季（3月~10月）：降雨量增加，位移增长率略高于其他时段
   • 水位下降+强降雨叠加：导致滑坡位移突变（如2012年3~6月JC15/JC24监测点）

3. 位移曲线特征
   • GNSS-3：反“S”型曲线（初始快→中期慢→后期加速）
   • JC15：稳定增长趋势（近似线性）
   • JC24：“S”型曲线（初始慢→中期加速→后期减缓）

3.2.2 相对表面位移分析

1. 监测点分布与数据特征

• 监测点位置：GNSS-4（下部）、GNSS-5（中部）、GNSS-6（上部）沿同一剖面布置
• 时间范围：2019年6月~2023年2月
• 相对位移定义：相邻监测点间的位移差值（如GNSS-4与GNSS-6的位移差）

2. 变形阶段划分

阶段	环境条件	位移特征	典型值
稳定阶段	低降雨量 + 库水位稳定	相对位移变化小（<5mm）	日均变化≤0.5mm
振荡阶段	强降雨 + 库水位升降	位移活跃，短期突变显著	峰值38.5mm（GNSS-4-6） 短期变化达18mm

3. 诱发因素影响

• 关键发现：
• 库水位下降期间，相对位移响应最显著（Pearson相关系数 -0.8~-0.9）
• 降雨与位移变化的滞后效应约3~7天
• 机制解释：
• 水位下降→坡体渗透压力增大→局部剪切变形加剧
• 降雨入渗→滑带土软化→抗剪强度降低

3.2.3 地表裂缝宽度

凉水井滑坡的地表裂缝宽度在监测期内整体呈扩大趋势，变化速度相对稳定。其中，滑坡后方的LF01监测点在2013年经历了两次突变，伴随水库水位显著下降和强降雨。裂缝宽度的累积变化最大出现在LF04监测点，达到94 mm，且靠近JC23监测点，地表位移更为明显。分析表明，裂缝宽度的变化对外部影响因素（如水位变化和降雨）响应较快，而表面位移的响应存在滞后性。

4 结果与分析

4.1 诱导因子分析与特征选择总结

对滑坡触发因素的相关性分析有助于筛选最优输入特征，以提高滑坡位移预测的准确性。研究表明，在雨季，凉水井滑坡的位移增量与降雨强度呈正相关关系，但存在一定的滞后效应。此外，水库水位波动同样影响滑坡变形，尤其是在水位下降时变形加速。由于滑坡体内的地下水作用，水库水位变化也存在滞后效应。因此，为解决多个因素及其滞后效应的复杂影响，预测模型需综合考虑降雨量、水库水位及其波动等输入变量。

随后，本文使用 Pearson 相关系数对三个主要影响因素中的 10 个子因素进行了相关性分析（图 11）。相关性较低的因素可能会引入噪声并降低预测的可靠性和准确性。因此，本文去除了相关性低的因子，最终选择了 9 个最优输入特征。这些特征包括 6 个外部触发因素 （Input2-Input7） 和 3 个表征滑坡蠕变行为的参数 （Input8-Input10） （图 12）

综上所述，本文将 6 个选定的外部触发因素与表征滑坡蠕变行为的 3 个参数整合在一起，形成一个全面的数据集。该数据集随后被用于训练 BG-CNN-LSTM 模型。输出变量是凉水井滑坡随时间变化的位移。

4.2 使用 BG-CNN-LSTM 进行滑坡位移预测

VIF、Gompertz 和 Weibull 模型用于拟合来自三种不同类型滑坡的变形位移数据。该过程旨在推导滑坡蠕变的特征参数，并确定滑坡变形破坏的阶段和类型。
对于 GNSS-3 监测点，实测滑坡位移数据对应于反向 “S” 型位移-时间曲线，并使用 VIF 模型进行拟合。
在 JC15 监测点的情况下，测得的位移数据与稳态型位移-时间曲线一致，并使用 Gompertz 模型进行拟合。
对于 JC24 监测点，实测位移数据符合“S”型位移-时间曲线，使用 Weibull 模型执行拟合。

举例来说，以稳定增长型滑坡为例，监测时间的增加导致模型曲线拟合精度的逐渐提高。如图 13 所示，它展示了在同一监测点上不同监测持续时间的 Gompertz 模型曲线拟合。因此，在选择监控数据时，建议选择相对较长的监控数据作为训练集。这种选择提高了拟合未来滑坡预测的蠕变特征参数的精度。我们选择使用初始 80% 的历史数据进行拟合和训练。

本研究从三个监测点中选择 3 个不同的时间跨度，以验证模型使用不同持续时间的数据集预测滑坡位移的普遍性和稳健性。该策略旨在探索模型在不同时间尺度上的性能，以确保其稳定性。此外，随着监测时间跨度的变化，可以将新的监测数据集成到相应的增长曲线模型中，以获得更新的滑坡蠕变特征参数。然后，这些参数可用于更新 BG-CNN-LSTM 动态智能预测模型。这种动态性使模型能够更灵活地适应不断变化的数据条件，从而增强其在预测中的泛化能力。

通过对 3 个监测点进行曲线拟合，得到训练集的起始和结束时间节点以及关键时间节点的蠕变特征参数，如表 1 所示。此外，它还显示了滑坡位移拟合的开始和结束时间节点，以及接近零的关键中间时间节点加速度。

可以得出结论，整体平滑拟合曲线模型能够较好地拟合滑坡位移，但不能反映滑坡位移的局部波动特征。此外，从拟合曲线模型得到的滑坡蠕变特征参数在预测监测期外的位移时可能具有显著的不确定性。因此，通过综合利用拟合过程中得到的滑坡蠕变特征参数和选择的最优输入变量，结合三个观测点的监测数据，开发并训练了BG-CNN-LSTM模型。根据经验，80% 的数据用于模型训练，20% 用于验证。

需要注意的是，滑坡验证集的蠕变特征参数来自训练集中的历史数据。该过程涉及通过生物生长模型将 80% 的历史位移数据合并到训练集中，作为数据增强过程。通过整合蠕变理论，确定了滑坡的变形阶段和未来变形趋势。获得的蠕变特性，然后，利用参数来预测未来的滑坡位移，提供预测性见解，同时增强模型的可解释性。

本研究使用 TCN-LSTM 模型、CNN-LSTM 模型和 BG-CNN-LSTM 动态智能系统三个增长曲线模型预测三个监测点的滑坡位移，如图 14 所示。分析表明，与增长曲线模型、TCN-LSTM模型和CNN-LSTM模型相比，在处理多类型滑坡数据时，BG-CNN-LSTM模型产生的预测结果与实际监测数据紧密吻合，表现出卓越的动态非线性预测性能和最高的准确性。与增长曲线模型不同，BG-CNN-LSTM模型更精确地捕捉了降雨量和库水位对滑坡变形的影响，有效地呈现了滑坡变形的短期波动特征。此外，与 CNNLSTM 和 TCN-LSTM 模型相比，BG-CNN-LSTM 模型结合了生物生长曲线来提取滑坡的蠕变特征参数，并进行数据增强以解决各种类型或阶段的滑坡。此外，它还集成了运动学因素和外部影响因素，显著提高了滑坡位移预测的准确性和鲁棒性。

BG-CNN-LSTM 模型的预测结果以及相关的误差值如图 15 所示。与实际测量值相比，三个监测点的位移预测表现出最小的差异。误差结果清楚地表明，在快速位移变化的阶段，BG-CNNLSTM 模型可以更准确地捕捉位移的局部波动，标准误差限制在较短的范围内。例如，在 JC24 监测点，2013 年 5 月和 8 月发生的两次突变的预测标准误差均低于其他三个模型的预测标准误差。此外，BG-CNN-LSTM 模型可以更精确地学习滑坡变形的细微波动，在大多数情况下保持相对较小且稳定的标准误差。

4.3 模型性能及准确率分析

TCN-LSTM模型、CNN-LSTM模型、BG-CNN- LSTM的预测误差结果三个测点（GNSS-3、JC15、JC24）的 动态智能系统如图 16 所示。分析小提琴图的结果，可以观察到，在三个模型中， BG-CNN-LSTM 模型表现出最佳的预测性能，数据分布最接近监测值，准确性最高。对于其他两种模型，在滑坡变形相对稳定的时期，CNN-LSTM 模型和 TCN-LSTM 模型更有效地捕捉了滑坡变形的演变趋势，表现出明显高于 BG 模型的预测准确性。图 16 中的阴影区域对应于滑坡位移频繁波动的时期，例如，在 2022 年 3 月、4 月和 5 月的 GNSS-3 监测点，由于库水位下降和频繁的集中降雨，滑坡位移变形表现出频繁的波动。在此期间，BG-CNN-LSTM模型的预测结果与监测数据最接近、最集中，预测精度最高，其次是CNN-LSTM模型和TCNLSTM模型，而VIF模型的预测精度最低。

预测模型的 MAE、MAPE 和 RMSE 结果如图 17 所示。从图中的误差分析可以得出结论，BGCNN-LSTM动态智能系统在四种模型中具有最小的预测误差和最高的精度，表明性能优越。具体而言，GNSS-3 监测点的 4 个模型的误差度量值差异最小，这可归因于在该监测点观察到的相对较小的滑坡位移。对于 JC15 监测点，4 种模型的 MAE、MAPE 和 RMSE 值差异最大。BGCNN-LSTM 模型的 MAPE 为 1.2%，比 CNN-LSTM 模型低 2.8%，比 TCNLSTM 模型低 2.9%，比 VIF 模型低 5.1%。RMSE 为 12.3，CNN-LSTM 下降了 30.5，TCN-LSTM 下降了 31.2，VIF 下降了 48.6。对于 JC24 监测点，BG-CNN-LSTM模型的MAE、MAPE和RMSE值显著低于其他两种模型，其他三种模型的差异相对较小。同时，模型的预测精度受监测点数据类型和监测时间长度的影响。然而，在不同情况下，BG-CNN-LSTM模型与其他两种模型相比，表现出明显更高的预测精度和鲁棒性，表明BG-CNN-LSTM具有较强的泛化能力。

5 讨论

本文介绍了一种创新方法，即 BG-CNN-LSTM 动态智能方法，用于预测凉水井滑坡的位移。

三种不同类型的生物生长曲线模型已集成到山体滑坡预测框架中。通过曲线拟合，得到滑坡蠕变特性参数（位移、速度和加速度）。然后将这些参数与外部触发因素（如水库水位波动和降雨量）相结合，以构建一个集成的数据集。该数据集被输入到 CNN-LSTM 模型中，以创建一个动态的智能预测系统。该方法同时考虑了滑坡的内在蠕变特性和外部触发因素，并将其整合到改进的 CNN-LSTM 模型中。这种方法为物理模型和深度学习模型的有机集成提供了一种新颖的视角。结果表明，与其他模型相比，这种方法提供了卓越的预测性能。

针对不同类型和阶段的滑坡，可以优化 BG 模型以提取蠕变特征参数并预测未来的变形趋势，从而显着增强滑坡位移预测的适应性。该方法集成了卷积神经网络 （CNN） 和长短期记忆 （LSTM） 网络，利用 CNN 强大的局部特征提取功能和 LSTM 对序列数据中的长期依赖关系进行建模的能力。它有效地捕捉了滑坡的蠕变特性，并从库层水位波动和降雨等外部因素中提取特征，表现出优异的时间序列预测性能。此外，该模型的参数共享和并行化特性增强了其检测实时局部波动的能力，有效地缓解了过度拟合，并提高了预测的稳健性和泛化能力。

由于监测周期的不同，累积滑坡位移曲线的特点可能会发生相应变化。在这种情况下，可以将新的监测数据输入到相应的增长曲线模型中，以获得修改后的模型参数。同时，水库水位波动、降雨量等新触发因素信息可用于更新BGCNN-LSTM动态智能系统。因此，通过不断整合复杂的多因素监测数据，BG-CNN-LSTM 模型从静态预测过渡到动态预测，增强了其对不断变化的条件的适应性。这种动态特性使模型能够更灵活地适应不断变化的数据条件，从而提高预测准确性和泛化能力。实时更新功能使 BG-CNN-LSTM 模型能够有效地解决实际应用中的波动和不确定性，从而产生更可靠的预测。

在未来的研究中，进一步的研究可能集中在增强多样化的生物生长模型，以提取滑坡的蠕变特征，同时实现与其他深度学习模型的更有效整合。此外，我们的目标是将这个综合模型扩展到更广泛的滑坡工程案例，利用广泛的监测数据来验证模型的预测性能。这种方法将为实际工程应用提供更可靠的理论支持和实际解决方案。

6 结论

本文将滑坡蠕变特性与非线性智能模型相结合，提出了BG-CNN-LSTM动态智能滑坡位移预测方法。本研究的主要结论如下：

（1）所提方法引入了蠕变理论，该理论考虑了滑坡变形特征和变形阶段，并改进了三个生物生长模型，能够更精确地提取滑坡蠕变参数，描述滑坡的未来运动趋势，提供预测性见解。

（2） 改进的 CNN-LSTM 模型首次被引入滑坡位移预测中。这种方法可以更有效地捕捉短期的剧烈波动和长期依赖性，从而更准确地预测未来的滑坡位移。

（3）提出了 BG-CNN-LSTM 动态智能滑坡位移预测方法。该方法将生物生长模型提取的滑坡蠕变特征参数与外部影响因子相结合，构建内外部综合数据集，并进行数据增强。同时，BG-CNN-LSTM不断更新新的监测信息，使预测系统由静态变为动态，可以更灵活地适应到具有长期动态变化的各种类型的位移数据。因此，它增强了模型在复杂滑坡环境中预测的稳健性。

（4）利用BG-CNN-LSTM预测三峡库区凉水井滑坡的位移。误差分析表明，BG-CNN-LSTM 表现出最高的预测准确性，超过了 BG、TCN-LSTM 和 CNN-LSTM 模型的预测性能。BG-CNN-LSTM 为预测多特征耦合滑坡中的位移提供了一种新的方法。

[1] Wang Z, Fang X, Zhang W, et al. Dynamic intelligent prediction approach for landslide displacement based on biological growth models and CNN-LSTM[J]. Journal of Mountain Science, 2025, 22(1): 71-88.