高频刷题-5. Longest Palindromic Substring

https://leetcode.com/problems/longest-palindromic-substring/

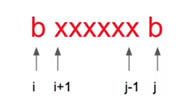
首先的一个概念是，上图是一个回文，有且仅有第i个字符 == 第j个字符 && 从i+1到j-1范围内的字符串也是回文。

也可以说，回文是中心对称的，即要么为中心对称(有中心节点)，要么为轴对称(没有中心节点)。

方法1: 动态规划

 

这样我们就可以推导出DP的状态方程:

我们维护一个二维数组 dp，其中 dp[i][j] 表示字符串区间 [i, j] 是否为回文串，当 i = j 时，只有一个字符，肯定是回文串，如果 i = j + 1，说明是相邻字符，此时需要判断 s[i] 是否等于 s[j]，如果i和j不相邻，即 i - j >= 2 时，除了判断 s[i] 和 s[j] 相等之外，dp[i + 1][j - 1] 若为真，就是回文串，通过以上分析，可以写出递推式如下：

 

dp[i, j] = 1                                  if i == j

 

      = s[i] == s[j]                          if j = i + 1

 

      = s[i] == s[j] && dp[i + 1][j - 1]          if j > i + 1     

 

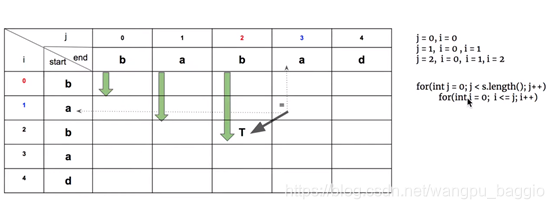
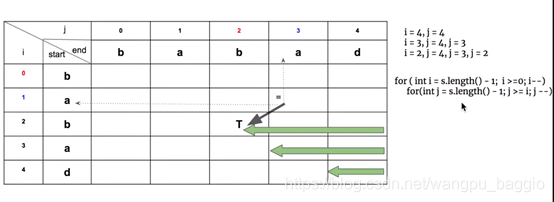
还有需要注意的是循环，因为计算下图[1, 3]位置的DP值时，需要用到[2, 2]的DP值。所以必须先有[2, 2]的值被计算出来。则循环需要有以下两种:

public String longestPalindrome(String s) {
        int len = s.length();
        boolean[][] dp = new boolean[len][len];
        char[] chars = s.toCharArray();
        String maxStr = "";

        for (int i = 0; i < len; i++) {
            dp[i][i] = true;
            maxStr = s.substring(i, i + 1);
        }

        for (int i = len - 1; i >= 0; i--)
            for (int j = i + 1; j < len; j++) {
                if (j == i + 1) {
                    if (chars[i] == chars[j]) {
                        dp[i][j] = true;
                        if (maxStr.length() < j - i + 1)
                            maxStr = s.substring(i, j + 1);
                    }
                } else if (i < len -1 && j > 1) {
                    dp[i][j] = dp[i+1][j-1] && (chars[i] == chars[j]);
                    if (dp[i][j]) {
                        if (maxStr.length() < j - i + 1)
                            maxStr = s.substring(i, j + 1);
                    }
                }
            }
        return maxStr;
    }

方法2: 中心扩展

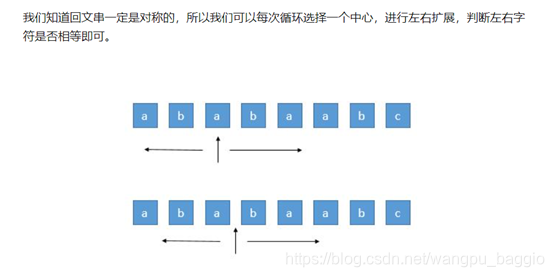
扩展的时候有两种可能性，1）扩展的是一个实际的值(回文为奇数)，2）扩展的起点是两个值的中间(回文为偶数)。因此扩展的时候，我们需要考虑这两种情况。这样遍历一次，每次计算i和i 到 i + 1两种情况下扩展的回文最大长度，将长度赋值到一个全局变量中。要特别注意扩展的结果和最后返回的start，end的index 下标。

private int[] range = new int[2];  // 记录最大回文的左右侧index
    
    public String longestPalindrome(String s) {
        
        int len = s.length();
        
        for (int i = 0; i < len; i++) {
            expandFromMiddle(s, len, i, i);
            expandFromMiddle(s, len, i, i + 1);
        }
        return s.substring(range[0], range[1]);  // 注意substring是[)的，不包含结束index的这个字符
    }

    // 从start 到 end 为中心的字符串，扩展出的回文长度
    private void expandFromMiddle(String s, int len, int start, int end) {

        int left = start, right = end;

        while(left >=0 && right < len && s.charAt(left) == s.charAt(right)) {
            left--;
            right++;
        }

        // 注意此时left 已经从回文中出去了一个，所以要 + 1； 
        // right也出去了一个，但是最终substring 只不包含range[1]的，所以不需要处理
        if (right - left  - 1 > range[1] - range[0]) {
            range[0] = left + 1;
            range[1] = right;
        }
    }

遍历一次，但是每一次经过了扩展计算，所以时间复杂度还是O(n^2)。

 

注意这里有个优化点，我们的expandFromMiddle()函数传递的是string s。JAVA中对象传递是引用的拷贝，所以每次调用这个方法都copy一份string，极大的影响执行时间，我们可以在开始的时候把string转成数组，这样传递的就是引用。所以可以减少拷贝的时间。

执行结果非常优：

private int[] range = new int[2];  // 记录最大回文的左右侧index
    
    public String longestPalindrome(String s) {
        
        int len = s.length();
        char[] ch = s.toCharArray(); // 转成数组，传递到函数中
        
        for (int i = 0; i < len; i++) {
            expandFromMiddle(ch, len, i, i);
            expandFromMiddle(ch, len, i, i + 1);
        }
        return s.substring(range[0], range[1]);  // 注意substring是[)的，不包含结束index的这个字符
    }

    // 从start 到 end 为中心的字符串，扩展出的回文长度
    private void expandFromMiddle(char[] ch, int len, int start, int end) {

        int left = start, right = end;

        while(left >=0 && right < len && ch[left] == ch[right]) {
            left--;
            right++;
        }

        // 注意此时left 已经从回文中出去了一个，所以要 + 1； 
        // right也出去了一个，但是最终substring 只不包含range[1]的，所以不需要处理
        if (right - left  - 1 > range[1] - range[0]) {
            range[0] = left + 1;
            range[1] = right;
        }
    }