本文详细介绍了八种经典的排序算法：冒泡排序、选择排序、直接插入排序、希尔排序、快速排序等，并提供了每种算法的基本思想、实现原理及特点。
目录
8 大排序算法
冒泡排序
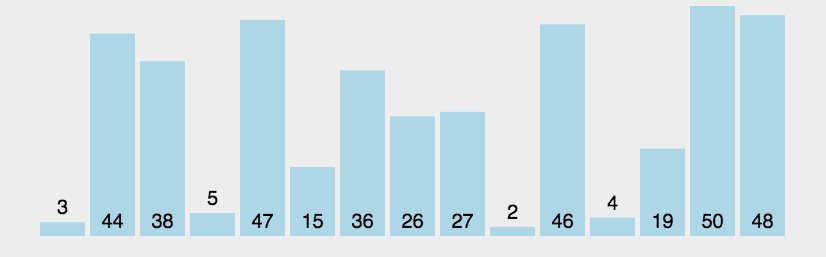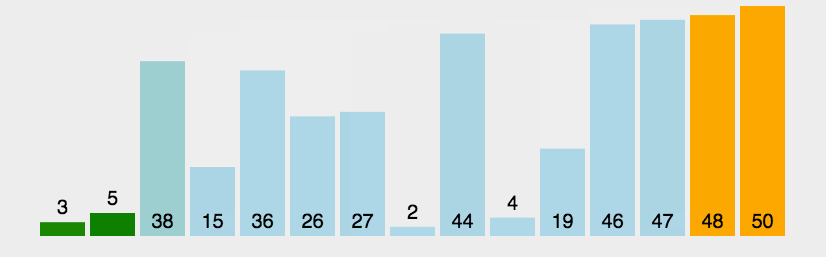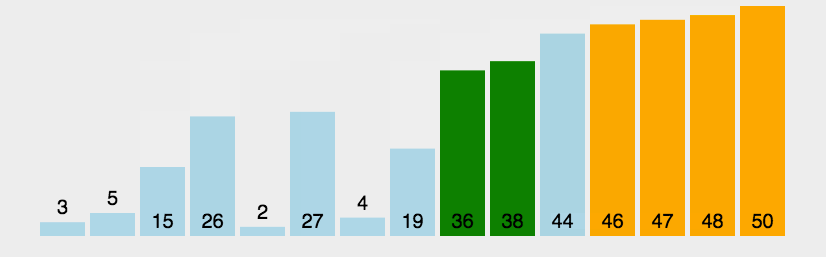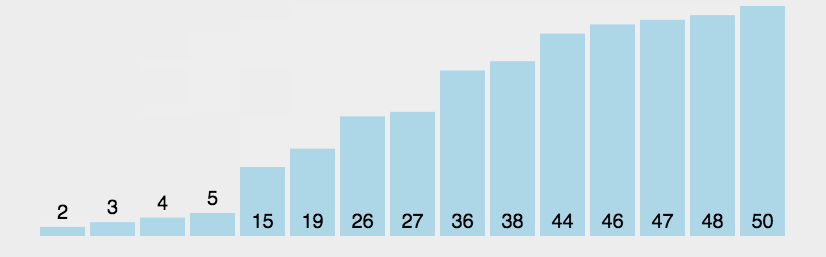
1、思想：每一趟将待排序序列中最大元素移到最后（反之也可以移动到最前），剩下的为新的待排序序列，重复上述步骤直到排完所有元素。
2、冒泡排序原理：
| ①、比较相邻的元素，如果第一个比第二个大，就交换他们两个。 ②、对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数（也就是第一波冒泡完成）。 ③、针对所有的元素重复以上的步骤，除了最后一个。 ④、持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。 |
3、特点：效率低，实现简单
/**
* 冒泡排序
* 1、比较相邻的元素。如果后一个比前一大，就交换位置。
* 2、最多比较的次数是：1+2+3+4+...+numbers.length-1
*
* @param numbers 需要排序的整型数组
*/
public static int[] bubbleSort(int[] numbers) {
//存放临时值
int temp;
int size = numbers.length;
for (int i = 0; i < size - 1; i++) {
for (int j = 0; j < size - 1 - i; j++) {
//< 表示倒序，> 表示顺序
if (numbers[j] < numbers[j + 1]) {
temp = numbers[j];
numbers[j] = numbers[j + 1];
numbers[j + 1] = temp;
}
}
}
return numbers;
}
选择排序
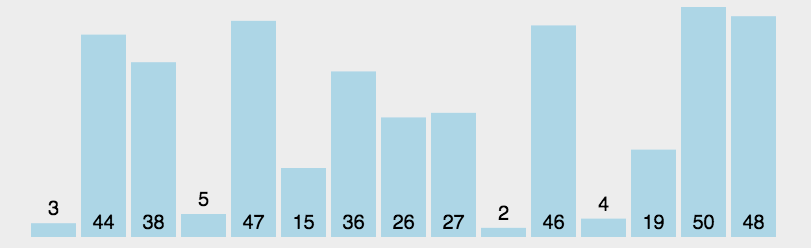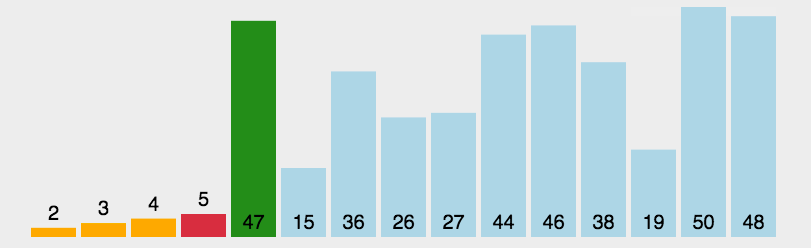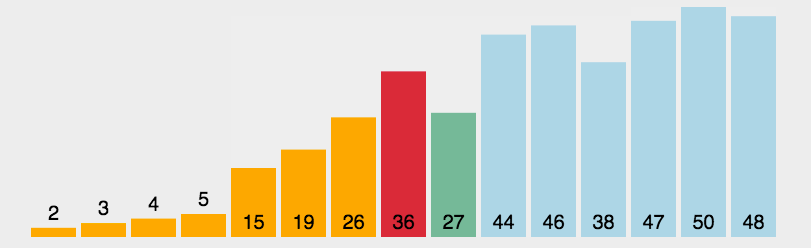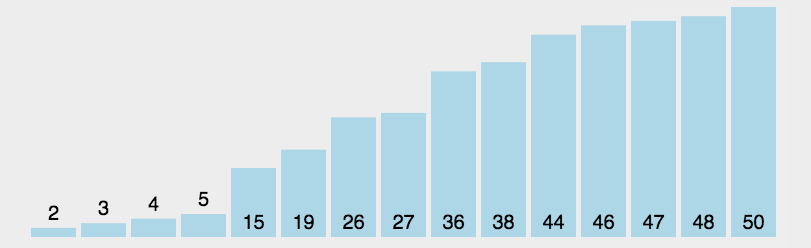
1、选择排序（Selection sort）是一种简单直观的排序算法。
2、选择排序原理：
| ①、初始时在序列中找到最小（大）元素，放到序列的起始位置作为已排序序列 ②、再从剩余未排序元素中继续寻找最小（大）元素，放到已排序序列的末尾 ③、以此类推，直到所有元素均排序完毕。 |
/**
* 假设待排序数组：{1, 23, 22, 12, 8}
* 选择排序
* 从左往右以第一个为基准，后面的元素轮流从末尾向前进行比对是否小于基准值，如果小于，则替换它们（同理也可以是大于）
* 第一轮排序，以"1"为基准，排序后：{1, 23, 22, 12, 8}
* 第二轮排序，以"23"为基准，排序后：{1, 8, 22, 12, 23}
* 第三轮排序，以"22"为基准，排序后：{1, 8, 12, 22, 23}
* 第四轮排序，以"22"为基准，排序后：{1, 8, 12, 22, 23}
*
* @param numbers
*/
public static int[] selectSort(int[] numbers) {
int size = numbers.length;
int temp;//存放比对过程中的临时值
for (int i = 0; i < size - 1; i++) {
int k = i;//k 位置表示临时的最小/大值
for (int j = size - 1; j > i; j--) {
if (numbers[j] < numbers[k]) {
k = j;
}
}
if (i != k) {
temp = numbers[i];
numbers[i] = numbers[k];
numbers[k] = temp;
}
System.out.println(Arrays.toString(numbers));
}
return numbers;
}直接插入排序
/**
* 直接插入排序
* 将第一个数和第二个数排序，然后构成一个有序序列
* 将第三个数插入进去，构成一个新的有序序列。
* 对第四个数、第五个数……直到最后一个数，重复第二步。
*
* @param numbers
*/
public static void insertSort(int[] numbers) {
//数组长度，将这个提取出来是为了提高速度。
int length = numbers.length;
int insertNum;//要插入的数
//插入的次数
for (int i = 1; i < length; i++) {
//要插入的数
insertNum = numbers[i];
//已经排序好的序列元素个数
int j = i - 1;
//序列从后到前循环，将大于insertNum的数向后移动一格
while (j >= 0 && numbers[j] > insertNum) {
//元素移动一格
numbers[j + 1] = numbers[j];
j--;
}
//将需要插入的数放在要插入的位置。
numbers[j + 1] = insertNum;
}
}希尔排序
/**
* 希尔排序
* 1、将数的个数设为n，取k=n/2，将下标差值为k的数分为一组，构成有序序列。
* 2、再取k=k/2 ，将下标差值为k的书分为一组，构成有序序列。
* 3、重复第二步，直到k=1执行简单插入排序。
*
* @param numbers
*/
public static void shellSort(int[] numbers) {
if (numbers == null || numbers.length <= 0) {
return;
}
int d = numbers.length;
while (d != 0) {
d = d / 2;
//分的组数
for (int x = 0; x < d; x++) {
//组中的元素，从第二个数开始
for (int i = x + d; i < numbers.length; i += d) {
//j为有序序列最后一位的位数
int j = i - d;
//要插入的元素
int temp = numbers[i];
//从后往前遍历。
for (; j >= 0 && temp < numbers[j]; j -= d) {
//向后移动d位
numbers[j + d] = numbers[j];
}
numbers[j + d] = temp;
}
}
}
}快速排序
/**
* 快速排序（效率最高，速度快）
* 1、选择第一个数为p，小于p的数放在左边，大于p的数放在右边。
* 2、递归的将p左边和右边的数都按照第一步进行，直到不能递归。
*
* @param numbers ：待排序的数组
* @param start ：排序的起始位置，比如 0
* @param end ：排序的结束位置，比如 numbers.length - 1
*/
public static void quickSort(int[] numbers, int start, int end) {
if (numbers == null || numbers.length <= 0 || start >= end) {
return;
}
// 排序的第一个数值作为基准值
int base = numbers[start];
// 记录临时中间值
int temp;
int i = start, j = end;
do {
while ((numbers[i] < base) && (i < end)) {
i++;
}
while ((numbers[j] > base) && (j > start)) {
j--;
}
if (i <= j) {
temp = numbers[i];
numbers[i] = numbers[j];
numbers[j] = temp;
i++;
j--;
}
} while (i <= j);
if (start < j) {
quickSort(numbers, start, j);
}
if (end > i) {
quickSort(numbers, i, end);
}
}
笛卡尔积
/**
* 笛卡尔积 演示 1
*
* @param allList ：格式 List<List<T>>，对每一个 List 子集合求笛卡儿积。从头开始，每两个求一次。
* 如 原数据：[[1, 2], [1, 2], [1, 2, 3], [1]]
* 笛卡尔积：
* [1, 1, 1, 1]
* [1, 1, 2, 1]
* [1, 1, 3, 1]
* [1, 2, 1, 1]
* [1, 2, 2, 1]
* [1, 2, 3, 1]
* [2, 1, 1, 1]
* [2, 1, 2, 1]
* [2, 1, 3, 1]
* [2, 2, 1, 1]
* [2, 2, 2, 1]
* [2, 2, 3, 1]
* @return
*/
public static List<List> descartes1(List<List> allList) {
if (allList == null || allList.isEmpty()) {
return new ArrayList<>();
}
if (allList.size() == 1) {
return allList.get(0);
}
// 组合的最终结果
List<List> result = new ArrayList();
// 第一个子集合，第1和第2个子集合合并后，list0 会变成 List<List> 格式.
List preList = allList.get(0);
for (int i = 1; i < allList.size(); i++) {
List list_i = allList.get(i);
// 前一个集合与后一个合并后的结果，一直到合并完成。
List tempList = new ArrayList();
// 每次先计算两个集合的笛卡尔积，然后用其结果再与下一个计算
for (int j = 0; j < preList.size(); j++) {
for (int k = 0; k < list_i.size(); k++) {
// 用于组装前一个集合中的每个元素与下一个求笛卡尔积
List cut = new ArrayList();
// 第1个集合和第2个集合合并时，preList 是 List，然后与第3个集合合并时，preList 是 List<List>
if (preList.get(j) instanceof List) {
cut.addAll((List) preList.get(j));
} else {
cut.add(preList.get(j));
}
cut.add(list_i.get(k));
tempList.add(cut);
}
}
// 第1个与第2个合并完成后，preList 就变成了 List<List>，然后继续与后面的子集合求笛卡尔积.
preList = tempList;
if (i >= allList.size() - 1) {
result = tempList;
}
}
return result;
}src/main/java/org/example/collection/List2Test.java · 汪少棠/java-se - Gitee.com
父子级递归
1、Java 实现树型数据递归，类似 Oracle 的 start with...connect by prior。
/**
* 查询某个节点下面的全部子孙节点(不含自己)——向下递归
*
* @param id ：节点ID
* @param treeDataList ：需要遍历的数据
* @return ：返回自己下面的全部子孙节点
*/
public List<TreeDataDO> getChildNodes(String id, List<TreeDataDO> treeDataList) {
List<TreeDataDO> returnDataList = new ArrayList<>();
for (TreeDataDO treeDataDO : treeDataList) {
if (StrUtil.equals(treeDataDO.getPid(), id)) {
// 添加子节点
returnDataList.add(treeDataDO);
// 递归添加子节点下面的子节点
returnDataList.addAll(getChildNodes(treeDataDO.getId(), treeDataList));
}
}
return returnDataList;
}
/**
* 查询某个节点上面的全部父、祖父节点(不含自己)——向上递归
*
* @param pid ：父节点ID
* @param treeDataList ：需要遍历的数据
* @return ：返回自己上面的全部父节点(包含父节点的父节点)
*/
public static List<TreeDataDO> getParentEleList(String pid, List<TreeDataDO> treeDataList) {
List<TreeDataDO> returnDataList = new ArrayList<>();
/**
* Optional.ofNullable(xxx).orElse(new ArrayList<>())：如果集合为null则返回一个空集合
* filter：返回条件成立的元素
* forEach：遍历集合
*/
Optional.ofNullable(treeDataList).orElse(new ArrayList<>())
.stream()
.filter(treeDataDO -> StrUtil.equals(treeDataDO.getId(), pid))
.forEach(treeDataDO -> {
// 添加父节点
returnDataList.add(treeDataDO);
// 递归添加父节点上面的父节点
returnDataList.addAll(getParentEleList(treeDataDO.getPid(), treeDataList));
});
return returnDataList;
}树型JSON数据：src/test/resources/data/recursionTreeData.json · 汪少棠/java-se - Gitee.com。
递归演示源码：src/test/java/org/example/se/RecursionTreeTest.java · 汪少棠/java-se - Gitee.com。
扫一扫
2075
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
