多标准优化的主动学习算法（Active learning through multi-standard optimization）——MSAL

主动学习的样本选择策略

主动学习在训练集中已标注数据上学习得到的知识作为先验信息，利用该先验知识对测试分布中未标注数据包含的信息进行判断，选择对模型训练最有力的数据集进行标注，已达到减少分类模型训练过程所需标注代价的目的。

目前，针对不同的应用领域，已经出现大量样本选择方法的研究工作。根据样本选择方法选取未标注样本的方式不同，可以将主动学习分为三种：成员查询综合（Membership Query Synthesis）、基于流（Stream-based）的主动学习和基于池（Pool-based）的主动学习。其中，基于池的样本选择方法应用最为广泛。而在基于池的主动学习中，主要有两种样本选择标准：信息量和代表性。

1. 信息量（Informativeness）
   衡量一个样本降低统计模型不确定性的能力。某个样本包含的信息越多，其信息熵越大，类别的不确定性也越高。查询最有信息性的实例是目前基于池的主动学习中最流行的选择策略，经典的算法包括委员会查询（Query-by-committee），最佳实验设计（Optimal experimental design）和不确定性抽样（Uncertainty sampling）等。
   有利于信息性的样本选择策略无法利用大量未标记的数据，查询样本的选择仅仅由少量已标记的样本来确定；容易选取离群点和异常点，而忽略分布密集区域类别很确定的样本，容易出现样本偏差和不理想的结果。
2. 代表性
   衡量一个样本是否能很好地代表未标记数据的整体输入模式。有利于代表性样本的方法，利用未标记数据的结构信息，其性能很大程度上取决于聚类结果的质量，可能需要在发现最优决策边界之前查询相对大量的样本，收敛缓慢。
3. 信息性+代表性
   黄圣军老师于2014年在顶会ICONIP上发表过一篇文章《Active learning by querying informative and representative examples》，该方法综合考虑了样本的信息性与代表性。我们使用作者提供给的代码，对选择到的训练集进行数据可视化后发现，该方法容易选到几个高相似度的训练样本，在一定程度上造成了标记浪费。
   因此，基于该发现，本文提出的算法在选择训练集样本时，额外考虑了训练集内部的差异性。

针对上述不足，本文提出了多标准优化的主动学习方法MSAL：

1. 改善有利于信息量的方法在选择样本时，倾向于选择离群点的可能性，避免出现样本偏差；
2. 改善有利于代表性的方法在选择样本点时，主要依赖于聚类结果的质量，倾向于选择聚类中心，在得到最有决策边界前需要查询大量实例，造成收敛缓慢的情况；
3. 选择样本时，考虑待选点与已选点之间的差异性，避免在同一类中重复选择不必要的样本，目的是提高所选择样本的多样性，减小标记代价，组成一个分类效果更好的训练集。

MSAL的样本选择策略

该约束优化问题提供了一种系统的方式来组合实例的信息性，代表性和多样性。
$$\{\begin{array}{r}\underset{x\in D_u}{\max }f(x)p(x)\\ s.t.g(x)-\beta \ge 0\end{array}$$其中 $f(x)$ 表示信息性， $p(x)$ 表示代表性， $g(x)$ 表示差异性， $\beta$ 表示差异性阈值。
首先，通过一个运行实例完整演示MSAL的流程：从210个实例中选择3%作为训练集。顶部显示输入的是 Seeds 数据集，该数据集通常用于标准的机器学习任务中。中间部分显示了多标准优化的主动学习方法，该算法综合考虑了实例的信息性，代表性和多样性。
经由数据可视化证明，仅考虑信息性或代表性，选择的实例或是片面的，无法代表整个数据集，或是标记冗余，浪费标注代价。
选择信息性与代表性乘积最大的实例，如果该实例满足差异性约束，则查询它的标签。
当给定的 $N$ 个标签用尽，循环终止。
底部显示的是输出，主动学习的输出为 $N$ 个关键实例的集合。
根据所选择的关键实例，使用最近邻（$k$-Nearest Neighbors，kNN）算法对剩余实例进行分类，得到分类准确率。
由此，所有的标记都被查询或预测完毕。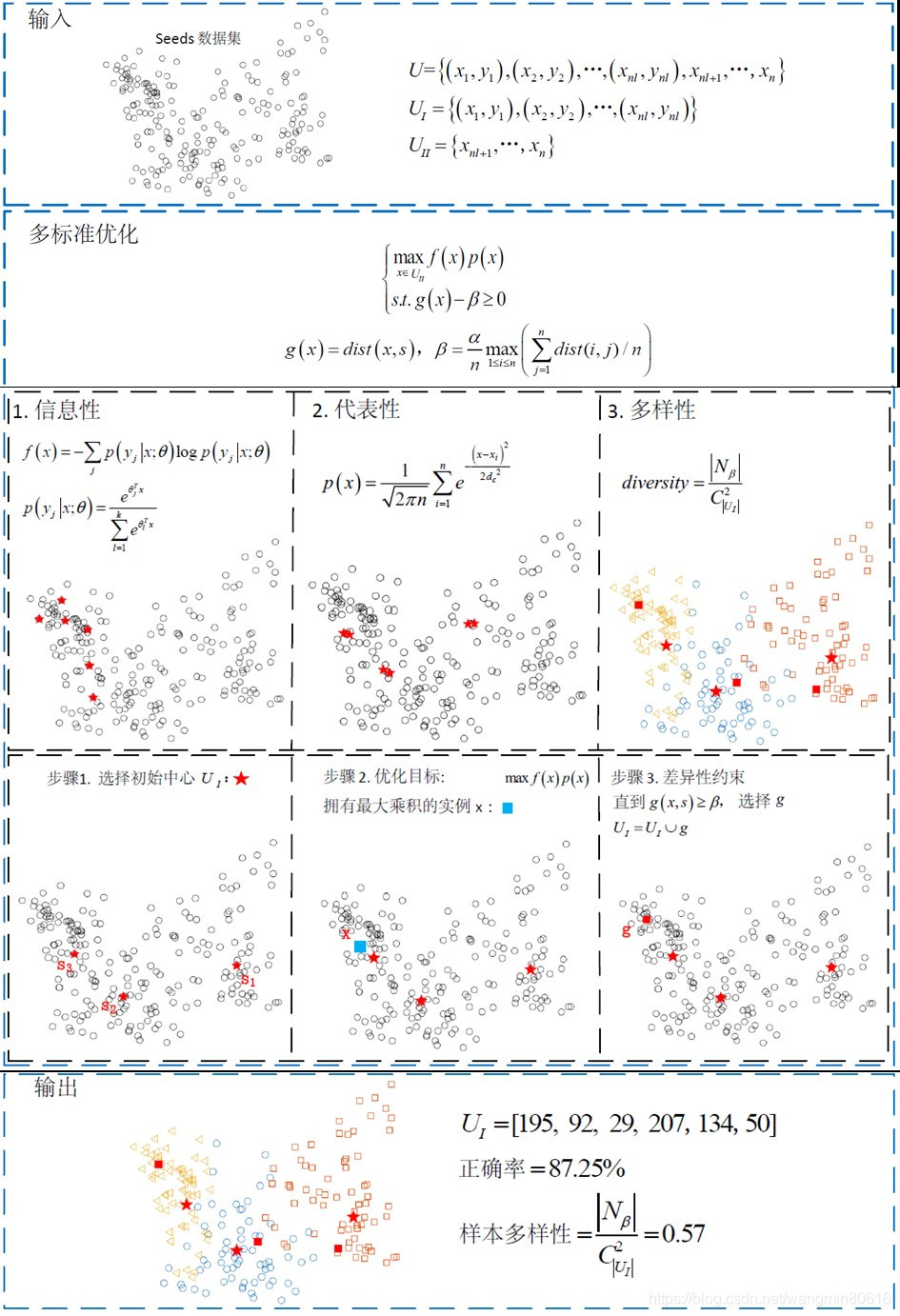

符号	意义	符号	意义
$U$	数据集 U =[$U_{\mathrm{I}}$, $U_{\mathrm{I}\mathrm{I}}$]	$s$	最近被标记的关键实例
$U_{\mathrm{I}}$	已标记数据集合	$f(x)$	实例 $x$ 的信息性
$U_{\mathrm{I}\mathrm{I}}$	未标记数据集合	$p(x)$	实例 $x$ 的代表性
$n$	数据集个数	$g(x)$	$x$ 的约束函数
$nl$	有标记的实例个数	$\beta$	差异阈值
$N$	专家可以提供的标签数量	$N_{\beta }$	显著差异集
$g$	满足差异性约束的实例

接下来，详细介绍信息性$f(x)$， 代表性$p(x)$ ， 训练集差异性$g(x)$ 的量化方法。

1. 信息性

信息量可以用来减少模型的不确定性。本文使用信息熵来测量实例 $x$ 的信息性。定义如下：
$$f(x)=-\sum _{j}P(y_j|x;\theta )\log P(y_j|x;\theta )$$其中 $P(y_j|x;\theta )$ 表示实例 $x$ 属于第 $j$ 个类别的概率。
考虑到多分类的问题，本文使用 soft-max 回归来计算某个实例的分类概率 $P(y_j|x;\theta )$。
令任意实例 $x$， $x$ 属于第 $j$ 个类别的概率 $y_j$ 等于
$$P(y_j|x;\theta )=\frac{e^{{\theta }_j^{T}x}}{{\sum }_{l=1}^k{e}^{{\theta }_l^{T}x}}$$计算 $P(y_j|x;\theta )$ 的关键在于参数 $\theta$ 的值，解决办法主要包括一下三个步骤。
步骤 1：决定代价函数 $J(\theta )$。
代价函数 $J(\theta )$ 表示预测值和真实值之间的偏差，代价函数表示为
J ( θ ) = − 1 n l [ ∑ i = 1 n l ∑ j = 1 k 1 { y i = j } log ⁡ e θ j T x i ∑ l = 1 k e θ l T x i ] J(\theta) = - \frac 1 {nl} \left[\sum_{i=1}^{nl} \sum_{j=1}^k 1\{ y_i = j\} \log \frac{e^{\theta_j^T x_i}}{\sum_{l=1}^k e^{\theta_l^T x_i}} \right] J(θ)=−nl1​[i=1∑nl​j=1∑k​1{ yi​=j}log∑l=1k​eθlT​xi​eθjT​xi​​]其中 i ∈ { 1 , 2 , ⋯   , n l } , j ∈ { 1 , 2 , ⋯   , k } i \in \{1, 2, \cdots, {nl}\}, j \in \{1, 2, \cdots, k\} i∈{ 1,2,⋯,nl},j∈{ 1,2,⋯,k}，$i$ 表示第$i$个实例，$j$ 表示类别。
1 { ⋅ } 1\{\cdot\} 1{ ⋅} 是一个指示函数，当判决正确时，结果为 1；其他情况，结果为 0。
步骤 2：通过获取最优参数 $\theta$ 来计算代价函数 $J(\theta )$。
为了最小化代价函数，必须要获取最优参数 $\theta$ 。
本文使用例如梯度下降或者柯西-牛顿（Quasi-Newton）这样的迭代优化算法来计算 $J(\theta )$。
通过一些推导，可以得到代表损失函数偏导数的梯度。 ∇ θ j J ( θ ) = − 1 n l ∑ i = 1 n l [ x i ( 1 { y i = j } − P ( y i = j ∣ x i ; θ ) ) ] {\nabla_{ {\theta_j}}}J(\theta) = - \frac{1}{nl}\sum_{i = 1}^{nl} {\left[{ {x_i}(1\{ {y_i} = j\} - P({y_i} = j\left| { {x_i};\theta} \right.))} \right]} ∇θj​​J(θ)=−nl1​i=1∑nl​[xi​(1{ yi​=j}−P(yi​=j∣xi​;θ))]通过迭代求解参数 ${\theta }_j$ ，可以获得收敛到 $J(\theta )$ 的模型参数，其中 ${\alpha }^{\prime }$ 是步长。$${\theta }_j:={\theta }_j-{\alpha }^{\prime }{\nabla }_{{\theta }_j}J(\theta ),j=1,2,\dots ,k$$步骤 3：计算假设函数 $h_{\theta }(x)$。
对每一个输入 $x$，假设函数都会给出分别属于类别 j j