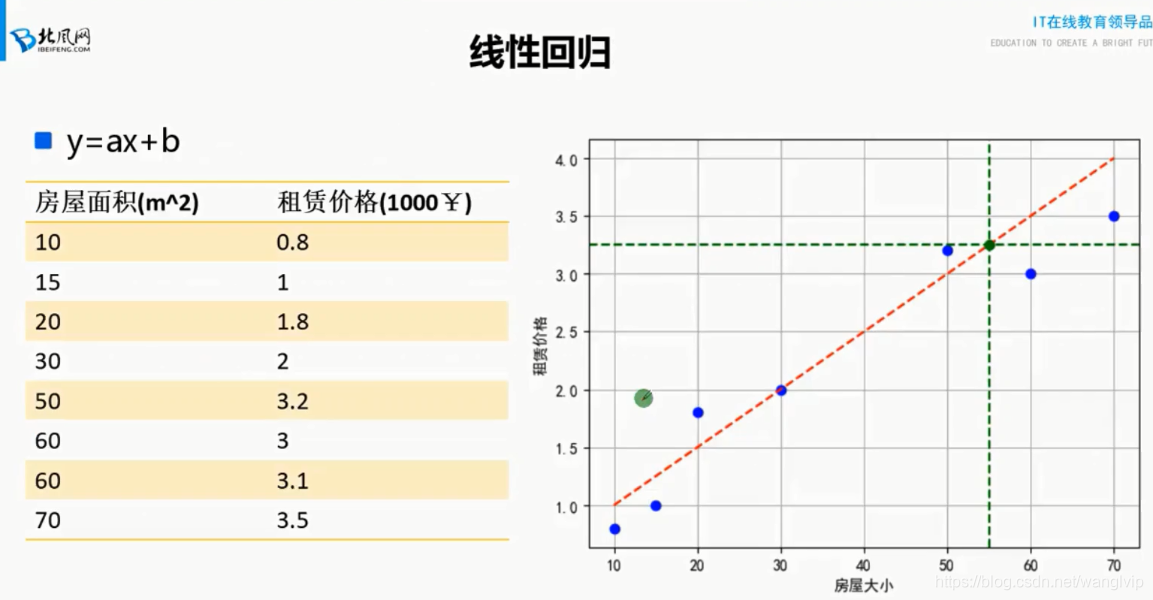
线性回归--上

线性回归：
    线性：函数(模型)参数的最高次项等于1(这也是数学中线性函数和非线性函数的概念)
    回归：最终要求计算出θ值，并选择最优的θ值构成算法公式

 

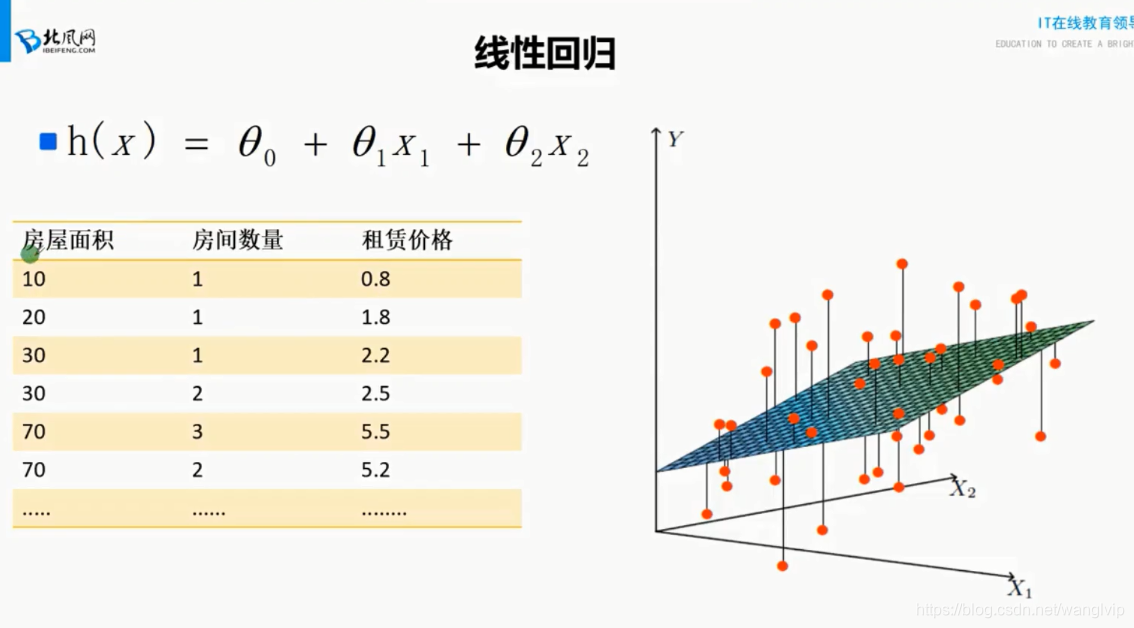
线性回归：
    实质上就是找x和y之间的线性关系，由于x(特征变量)和y(预测值)都是已知的,
    那么找的就是的θ最优值

独立：不同样本之间的预测值/误差值是相互独立的，没有任何关系
同分布：一个样本在不同的特征上的误差是同分布的
均值为零: 线性回归的目的是让函数均匀的分布在样本的两侧, 两边的误差值可以正负抵消；
         最理想的就是从1-m个样本的误差平方和e等于0(则误差均值e/m也为0) 

 

 

 

 

** 00:29:03-00:59:37 讲解求解过程

**00:59:00-01:06:39 如何在官网下载案例的训练数据

 最小二乘.py

import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

from sklearn.model_selection import train_test_split

# 设置字符集，防止中文乱码
mpl.rcParams['font.sans-serif'] = [u'simHei']
mpl.rcParams['axes.unicode_minus'] = False

# 加载数据
path = '../datas/household_power_consumption_1000.txt'
df = pd.read_csv(filepath_or_buffer=path, sep=';')
# 查看一下info信息
# print(df.info())
# print(df.head(5))

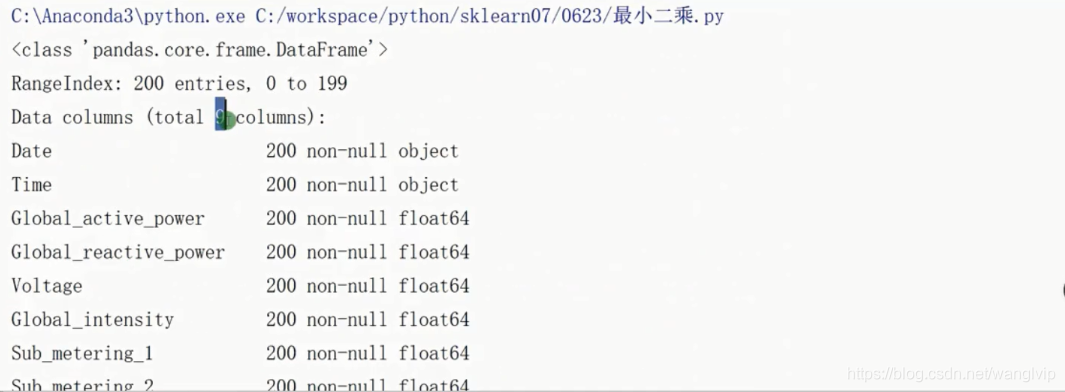
# 获取功率的值作为特征属性X，获取电流的值作为目标属性Y
X = df.iloc[:, 2:4]
Y = df.iloc[:, 5]
# print(X.head(5))
# print(Y)

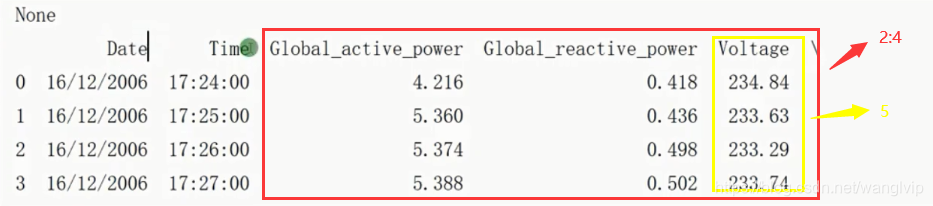
# 将数据分成训练集和测试集
# random_state：随机数种子，保证在分割数据的时候，多次执行的情况，产生的数据是一样的
x_train, x_test, y_train, y_test = train_test_split(X, Y,
    train_size=0.8, random_state=0)
print(x_train.shape)
print(type(x_train))
print(x_test.shape)
print(y_train.shape)
print(y_test.shape)

# 模型构建
# 1. 使用numpy的API讲DataFrame转换成为矩阵的对象
x = np.mat(x_train)
y = np.mat(y_train).reshape(-1, 1)
print(y.shape)
print(type(x))

# 2. 求解析式
theta = (x.T * x).I * x.T * y
print(theta)

# 使用模型对数据做预测
y_hat = np.mat(x_test) * theta

 

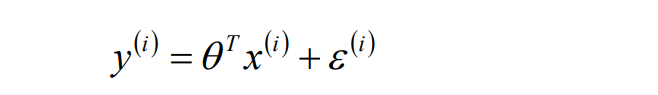
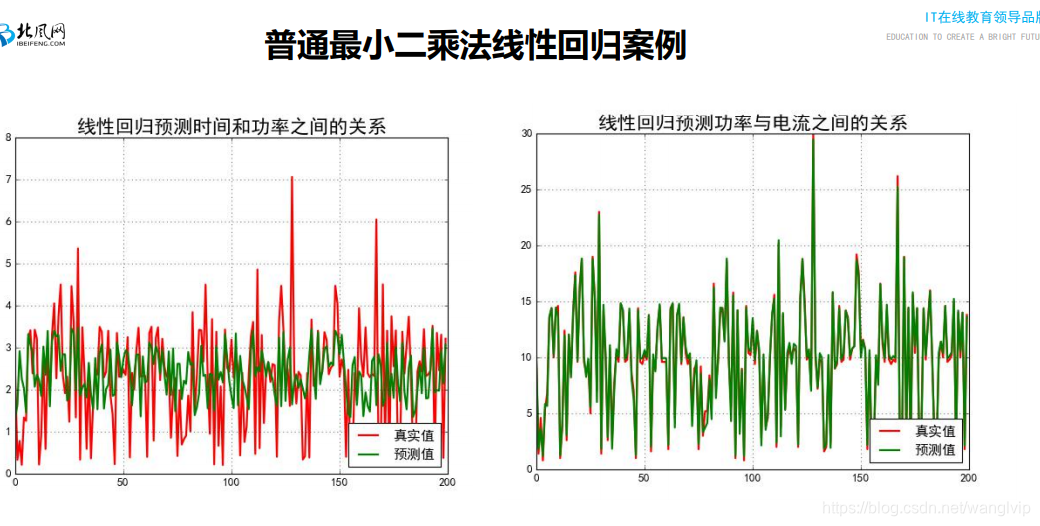
# 画图看一下效果如何
t = np.arange(len(x_test))
plt.figure(facecolor='w')
plt.plot(t, y_test, 'r-', linewidth=2, label=u'真实值')
plt.plot(t, y_hat, 'g-', linewidth=2, label=u'预测值')
plt.legend(loc='lower right')
plt.title('线性回归')
plt.show()

04_案例代码：使用ScikitLearn相关算法API实现案例代码及机器学习代码编写流程

案例代码：使用ScikitLearn实现普通最小二乘线性回归算法案例代码

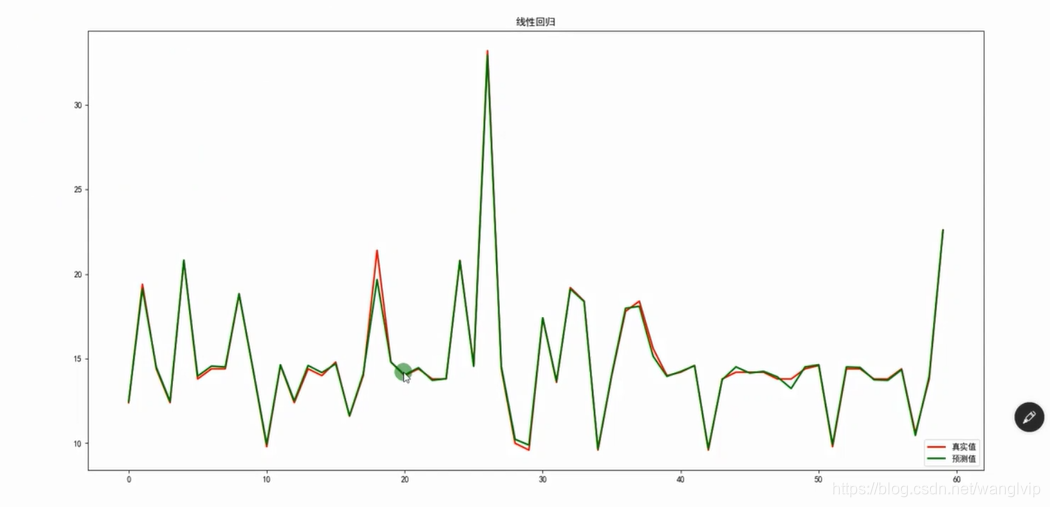 05_案例代码：使用ScikitLearn实现普通最小二乘线性回归算法案例代码讲解

**1:52:33-官网上线性回归算法的用法

 

10_案例代码：分类案例综合代码讲解

 

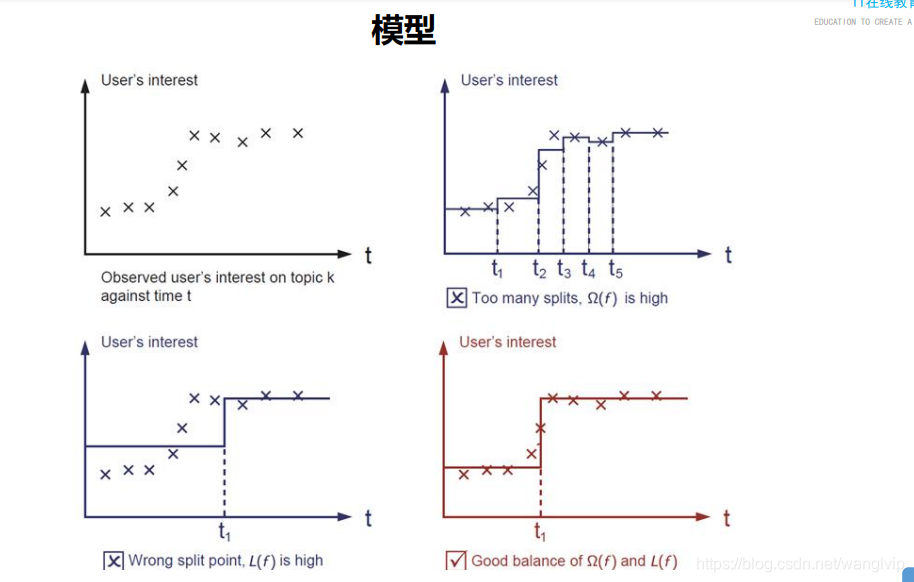
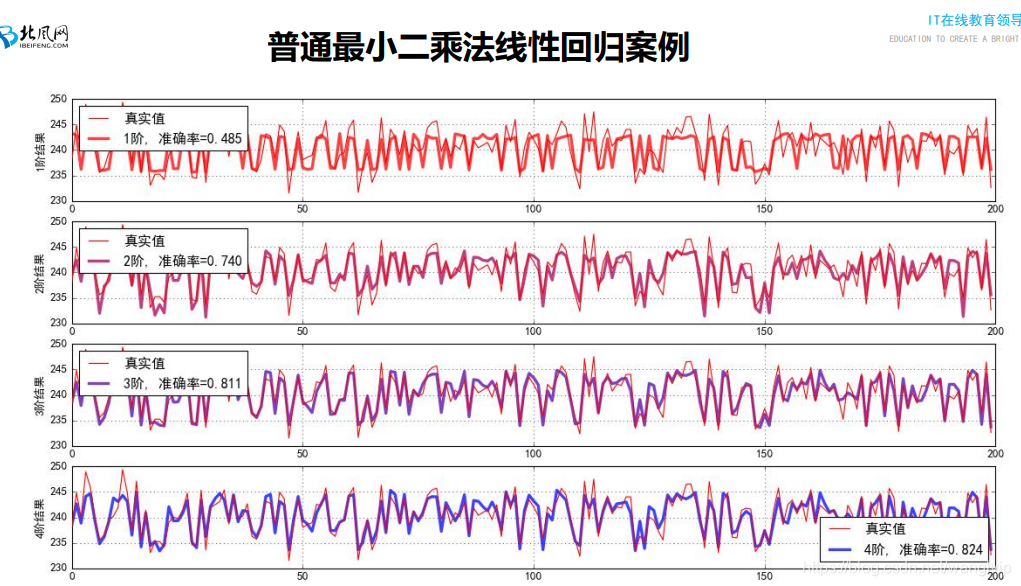
1.每两个点预测值的平均值作为预测值；
2.通过阈值t,小于t的所有值求平均值作为预测值，大于t亦求之。
注意：2图是过拟合  3图是欠拟合

 如何解决欠拟合和过拟合？ 

如果模型误差比较大，就表示模型存在欠拟合的问题：
  导致的原因：
    -1. 算法的学习能力太差
	-2. 数据太少
	-3. 特征属性太少(现有特征属性和目标属性之间的关系可能没有那么强)
  解决方案：
    -1. 换一种学习能力强的算法
	-2. 增加样本数据
	-3. 增加特征属性

如何增加特征属性？

多项式扩展：
  功能：将低维空间的数据通过多项式的变换，映射到高纬度的空间中
  效果：可以将低维空间非线性的数据转到到高维空间变成线性数据
  eg:
     原始数据：(2,3)
	 做一个最高次为2的多项式变换，得到的结果就是：(2,3,4,9,6)
	 做一个最高次为3的多项式变换，得到的结果就是：(2,3,4,9,6,8,27,12,18)

**03:13:-03:14 讲解多项式扩展的代码实现

通过增加维度来让非线性数据变成线性数据

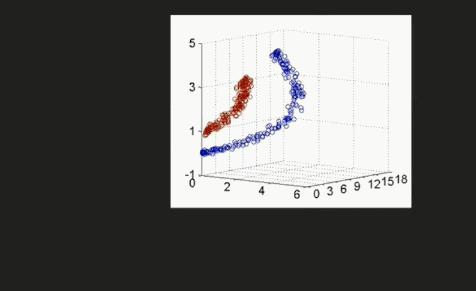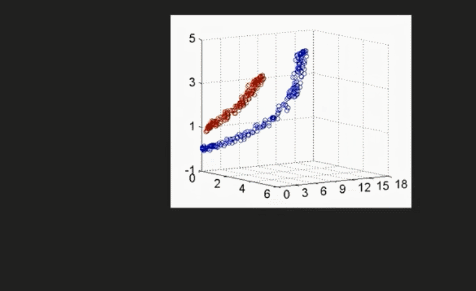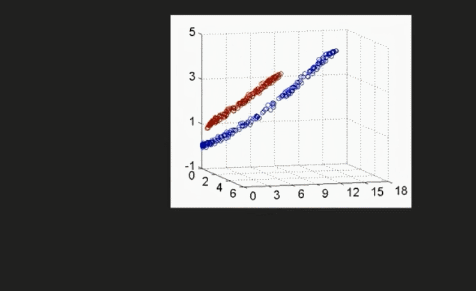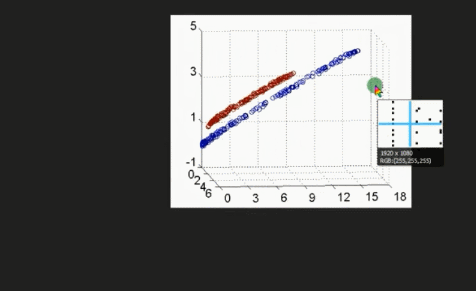
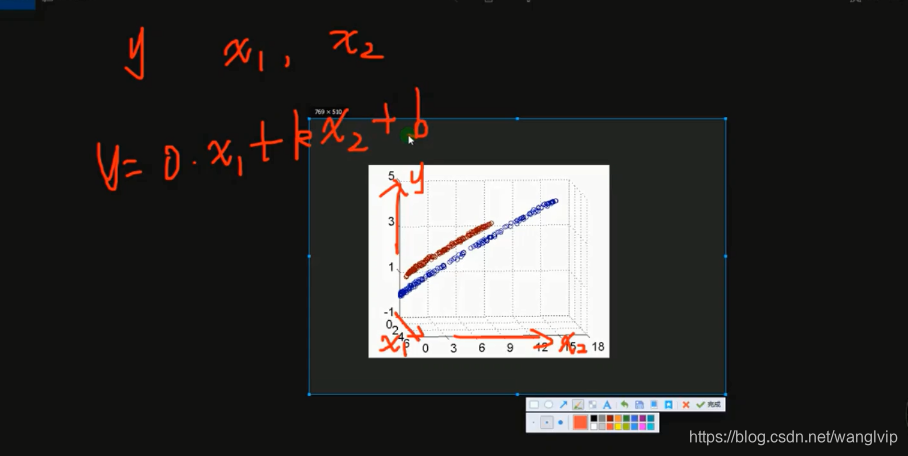
代码讲解：03:22-

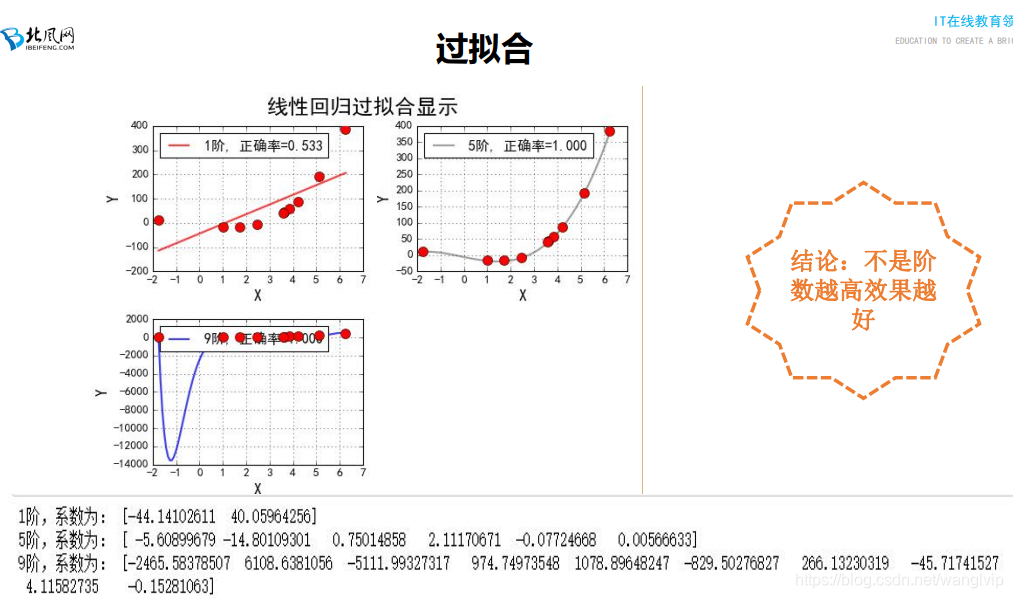
注意： 1、 要求不仅让损失函数越小越好，限制θ值也不要过大
      2、 θ值不要过大

正则项又叫惩罚项：
    要求损失函数足够小，θ也不能太小
    λ是学习率表示正则项对最终结果的影响
       1、如果λ=0.0001的话,θ就可以稍微大一点
       2、如果λ=10的话,θ就得足够小

原理：
    在模型尽量靠近最优解的情况下，模型也不至于太复杂(通过稀疏解来去除一些特征，使模型
    不至于太复杂)

注意：加上正则项就不在是线性回归
     正则回归：只有损失函数，是基于矩阵分解来求解
     如果损失函数后面加上L1正则，称作岭回归
     如果损失函数后面加上L2正则，称作LASSO回归

稀疏解：系数等于0
稀疏解对最终的值没有预测能力，可以去除
L1容易有稀疏解，L2不容易有稀疏解
鲁棒性：预测能力的稳定性
特征工程中做特征选择、降维操作去删除冗余的的特征,这时候L2更优质(前提是已经删除了冗余的特征)

 

 

 

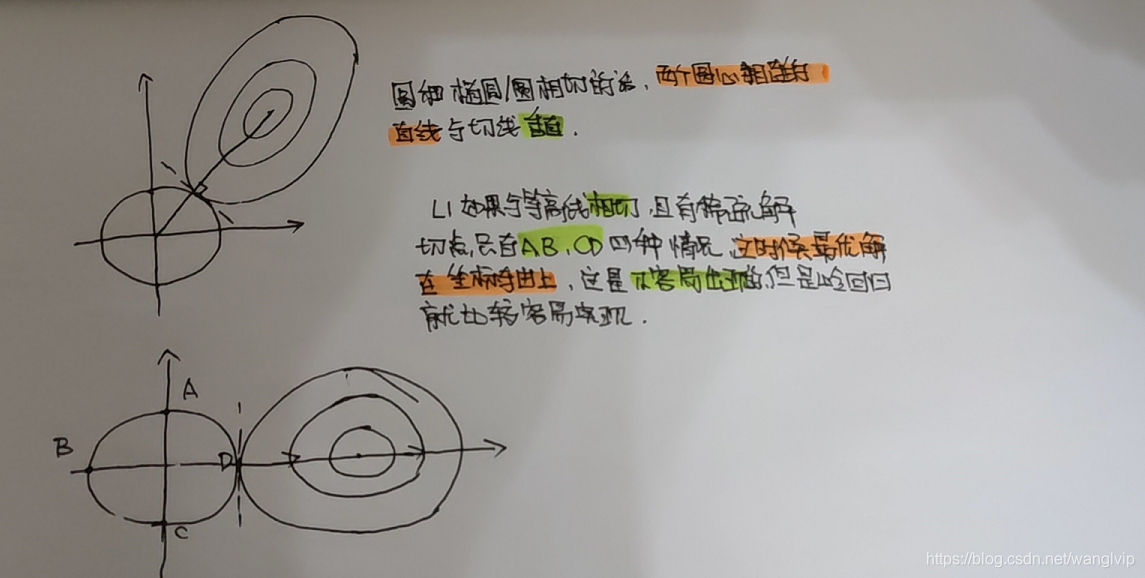
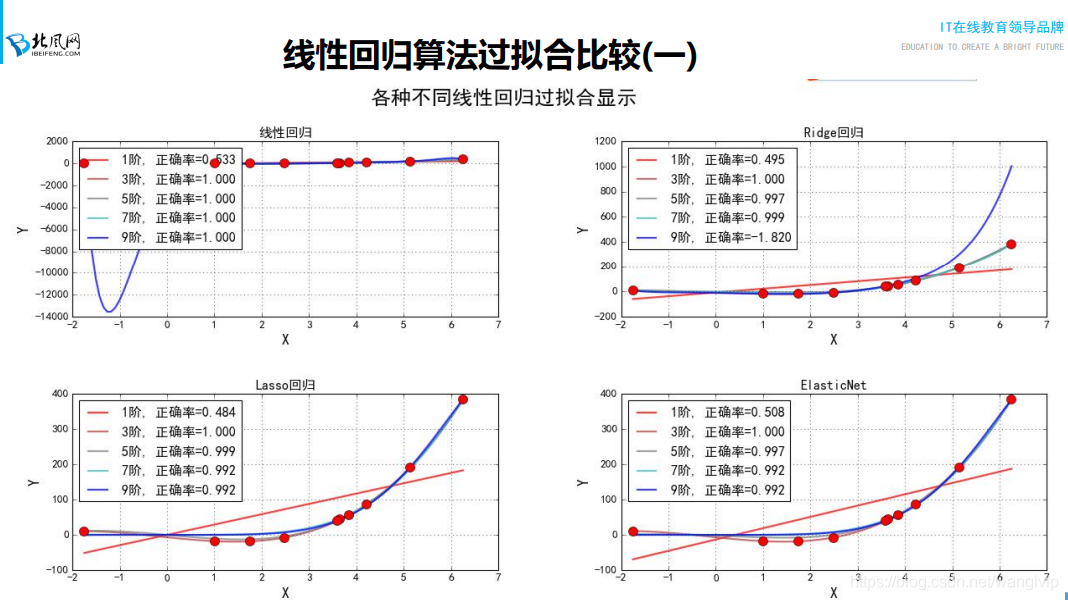
**04:14-04:36 讲解线性回归算法过拟合比较代码

 09_回归算法模型评估指标、超参给定以及交叉验证讲解

 

RMSE可以得到更具体的值(基本就可以看做实际值和预测值之间的差距),一般情况下比MSE用的更多
工作中第三种用来评估模型最多(source方法)
方差足够大的情况下误差比较大也是会被认可的??? 04:44
**04:45 讲解第三种应用的api source的用法

 

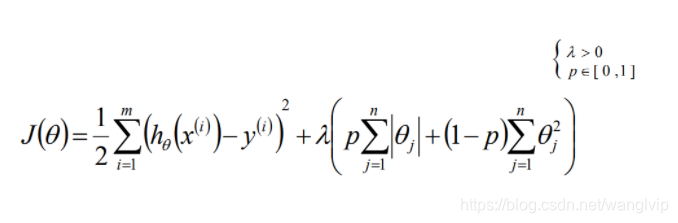
θ：是模型参数，表示数据之间的映射关系
λ：正则化学习率(影响的权重)
P：正则化中L1和L2占有的权重

调参、超参：
  给定算法模型训练过程中给定的模型相关的参数，但是这个参数不是模型参数(不是数据分布参数)。
  方案：
    -1. 可以根据算法的特性、业务的背景，根据经验给定。
	-2. 通过交叉验证的方式来选择最优参数
	-3. 网格参数选择

***04:51-04:49 讲解如何理解上式

K折交叉验证(K-Fold)
  注意：是在模型训练过程中进行的，主要用于参数的选择。
  方式：
    -1. 将fit传入的训练数据集划分为K份
	-2. 对当前的模型参数，使用其中的k-1份数据用训练模型，用训练好的模型在另外1份数据
    上进行模型效果的评估(直接调用模型的score方法)，迭代执行K次，得到K个score方法执行
    的值，将这K个值求均值作为当前参数在当前数据集上的模型效果。
	-3. 对另外一组参数采用和第二步一样的操作，得到对应的score均值。
	-4. 对所有参数模型对应的均值score，选择值最大的作为最优score，对应的模型参数也就
    是最优的模型参数
  eg：
    alphas=[0.1,0.2,0.3], l1_ratio=[0.0,0.5], K=3
	-1. 当前参数：alpha=0.1, l1_ratio=0.0,
	  --1. 训练集：1,2; 测试集: 3 -> score11
	  --2. 训练集：1,3; 测试集: 2 -> score12
	  --3. 训练集：2,3; 测试集: 1 -> score13
	  --4. 求score的均值: score1 = (score11 + score12 + score13)/3

	-2. 当前参数：alpha=0.1, l1_ratio=0.5, 
	  --1. 训练集：1,2; 测试集: 3 -> score21
	  --2. 训练集：1,3; 测试集: 2 -> score22
	  --3. 训练集：2,3; 测试集: 1 -> score23
	  --4. 求score的均值: score2 = (score21 + score22 + score23)/3

	-3. 当前参数：alpha=0.2, l1_ratio=0.0, 
      --1. 训练集：1,2; 测试集: 3 -> score31
	  --2. 训练集：1,3; 测试集: 2 -> score32
	  --3. 训练集：2,3; 测试集: 1 -> score33
	  --4. 求score的均值: score3 = (score31 + score32 + score33)/3

	-4. 当前参数：alpha=0.2, l1_ratio=0.5, 
	  --1. 训练集：1,2; 测试集: 3 -> score41
	  --2. 训练集：1,3; 测试集: 2 -> score42
	  --3. 训练集：2,3; 测试集: 1 -> score43
	  --4. 求score的均值: score4 = (score41 + score42 + score43)/3

	-5. 当前参数：alpha=0.3, l1_ratio=0.0, 
	  --1. 训练集：1,2; 测试集: 3 -> score51
	  --2. 训练集：1,3; 测试集: 2 -> score52
	  --3. 训练集：2,3; 测试集: 1 -> score53
	  --4. 求score的均值: score5 = (score51 + score52 + score53)/3

	-6. 当前参数：alpha=0.3, l1_ratio=0.5, 
	  --1. 训练集：1,2; 测试集: 3 -> score61
	  --2. 训练集：1,3; 测试集: 2 -> score62
	  --3. 训练集：2,3; 测试集: 1 -> score63
	  --4. 求score的均值: score6 = (score61 + score62 + score63)/3
	最优模型参数：在六组参数中，选择score最大的一组参数最优最优模型参数。

留一交叉验证--了解,工作中基本不用：
  其实就是n折交叉验证(n是样本数)
  含义：从训练集中抽取一个样本作为验证数据，其它的n-1条样本作为模型训练数据