BM1 反转链表-优快云博客

本文介绍了三种反转单链表的方法：使用栈、双指针和递归。栈法通过压栈和出栈实现反转；双指针法通过左右指针交换节点连接；递归法从尾到头或头到尾改变节点指向。所有方法时间复杂度均为O(n)，但空间复杂度不同，栈和递归法为O(n)，双指针法为O(1)。

内容描述：

给定一个单链表的头结点pHead(该头节点是有值的，比如在下图，它的val是1)，长度为n，反转该链表后，返回新链表的表头。

数据范围：

0≤n≤1000
要求：空间复杂度 O(1)，时间复杂度O(n)
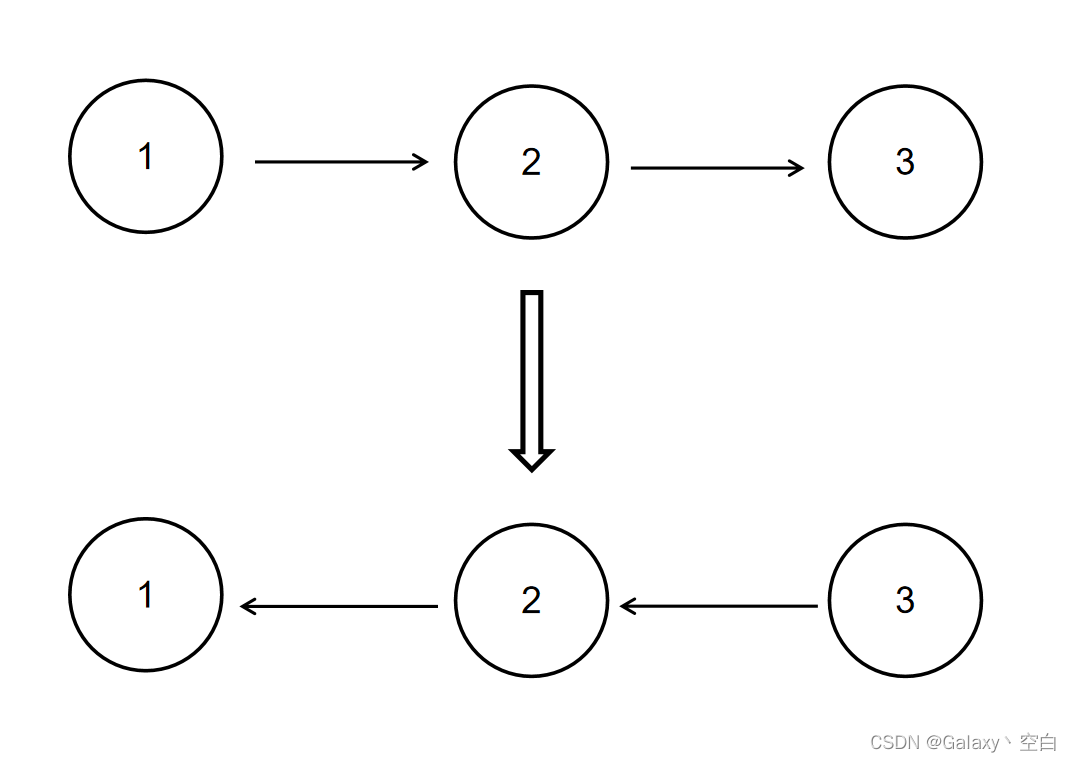
如当输入链表{1,2,3}时，
经反转后，原链表变为{3,2,1}，所以对应的输出为{3,2,1}。
以上转换过程如下图所示：
在这里插入图片描述

解题关键：栈，双指针，递归

1. 栈

栈先进后出的特点刚好满足我们的需要，依次取出链表的值然后依次放到栈中，然后再从栈中以此取出就得到了我们想要的反装效果。
借助了Java中提供的栈类，借助该类后我们要熟记该类的几个重要方法，push()压栈，pop()出栈，isEmpty()栈是否为空。

/*
public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}*/
public class Solution {
    public ListNode ReverseList(ListNode head) {
    	// 创建一个栈
        Stack<ListNode> stack = new Stack();
        // 将链表入站
        while(head!=null) {
			stack.push(head);
			head = head.next;
		}
		// 如果传入的为空直接返回空
		if(stack.isEmpty()) return null;
		// 临时变量存储结果的头结点
		ListNode temp = stack.pop();
		// 把temp赋值给result，因为下面会操作temp
		// 链接后面的值，而我们只要头节点即可
		ListNode result = temp;
		// 循环继续取出栈中剩下的节点,依次链接
		while(!stack.isEmpty()) {
			temp.next = stack.pop();
			temp = temp.next;
		}
		// 断掉最后一个的next值,因为入站时没有断，会形成循环链表
		temp.next = null;
		return result;
    }
}

时间复杂度：

将每个节点推入堆栈的 while 循环运行 N 次，其中 N 是原始链表的长度。
弹出每个节点并将它们链接在一起的 while 循环也运行了 N 次。
while 循环内部的操作需要常数时间。
因此，总的时间复杂度为 O(N)。

空间复杂度：

该方法使用一个堆栈来存储原始链表的所有节点。堆栈的最大大小为 N，其中 N 是原始链表的长度。
该方法创建一些 ListNode 变量来存储临时结果，但它们需要常量空间。
因此，总的空间复杂度为 O(N)。

总之，该方法的时间复杂度为 O(N)，空间复杂度也为 O(N)。

2.双指针

双指针思想使用两个指针一左一右，初始化时左面为空，右面为头结点。然后将右面的next值指向左面的null，左右指针向前移动一位，继续执行改操作直到右指针到链表尾部。

/*
public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}*/
public class Solution {
    public ListNode ReverseList(ListNode head) {
        if(head==null)
            return null;
        // 定义两个指针
        ListNode left = null;
        ListNode right = head;
        while(right!=null) {
        	// 记录一下头结点的下一个节点
            ListNode temp = cur.next;
            // 改变头节点的指向
            right.next = pre;
            // 左右指针向前移动
            left = right;
            right = temp;
        }
        return pre;
    }
}

时间复杂度：

该方法使用一个 while 循环来遍历原始链表中的每个节点，因此循环运行的次数取决于原始链表的长度 N。
每个节点的指针需要改变指向，这些操作的时间复杂度是常数级别的。因此总的时间复杂度是 O(N)。

空间复杂度：

该方法使用了两个指针变量 left 和 right，以及一个 ListNode 变量 temp，它们都只需要常数级别的额外空间，因此空间复杂度为 O(1)。
方法没有使用任何数组或堆栈来存储额外的数据，所以空间复杂度是常量级别的。

综上所述，该方法的时间复杂度为 O(N)，空间复杂度为 O(1)。

3.递归

普通递归

普通递归的思想是从链表的尾部向头部开始反转，首先不断递归直到找到链表最后一个节点的前一个节点，然后把该节点的next即尾节点的next指向自己完成反转，然后把该节点的next置为空，防止成环。reverse的头结点即是链表的最后一个节点。

/*
public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}*/
public class Solution {
    public ListNode ReverseList(ListNode head) {
    	// 判断是否走到最后一个节点和前一个节点
        if(head == null || head.next == null)
            return head;
        // 递归调用
        ListNode reverse = ReverseList(head.next);
        head.next.next = head;
        head.next = null;
        return reverse;
    }
}

时间复杂度：

该方法使用了递归来反转单链表，每次递归都会处理链表中的一个节点，因此递归深度取决于链表的长度 N。
在递归过程中，每个节点的指针需要改变指向，这些操作的时间复杂度是常数级别的，因此总的时间复杂度是 O(N)。

空间复杂度：

该方法使用了递归，每次递归需要使用系统栈来存储递归调用的上下文，因此递归深度是 O(N)。
在每次递归中，方法只创建了常数级别的 ListNode 变量 reverse，因此除了系统栈外，空间复杂度是常数级别的。

综上所述，该方法的时间复杂度为 O(N)，空间复杂度为 O(N)。需要注意的是，在极端情况下，递归深度可能达到链表的长度，因此该方法可能会导致栈溢出。

尾递归

尾递归是递归的一种优化，调用递归时存储上一步操作的结果而不是再去计算展开式。
解题方法和普通递归操作相反，尾递归从链表的头部开始反转

/*
public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}*/
public class Solution {
    public ListNode ReverseList(ListNode head) {
        return reverseListMain(head,null);
    }
	// 这是一次全部出栈的实现
    public ListNode reverseListMain(ListNode cur,ListNode pre){
        if (cur == null)
            return pre;
        // 记录当前节点的下一个节点否则执行完下一步会丢失
        ListNode next = cur.next;
        // 当前节点的下一个为前一个节点
        cur.next = pre;
        return reverseListMain(next,cur);
    }
    // 这里又可以一次一个出栈
    public ListNode reverseListMain2(ListNode cur,ListNode pre){
        if (cur == null)
            return pre;
        // 记录当前节点的下一个节点否则执行完下一步会丢失
        ListNode next = cur.next;
        // 当前节点的下一个为前一个节点
        cur.next = pre;
        ListNdoe node = reverseListMain2(next,cur);
        return node;
    }
}