LeetCode每日一题(1857. Largest Color Value in a Directed Graph)

There is a directed graph of n colored nodes and m edges. The nodes are numbered from 0 to n - 1.

You are given a string colors where colors[i] is a lowercase English letter representing the color of the ith node in this graph (0-indexed). You are also given a 2D array edges where edges[j] = [aj, bj] indicates that there is a directed edge from node aj to node bj.

A valid path in the graph is a sequence of nodes x1 -> x2 -> x3 -> … -> xk such that there is a directed edge from xi to xi+1 for every 1 <= i < k. The color value of the path is the number of nodes that are colored the most frequently occurring color along that path.

Return the largest color value of any valid path in the given graph, or -1 if the graph contains a cycle.

Example 1:

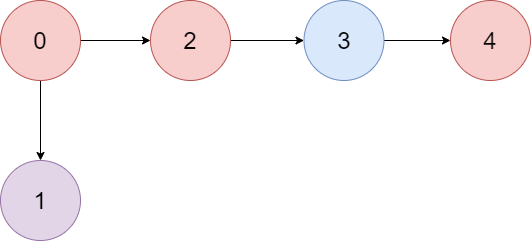
Input: colors = “abaca”, edges = [[0,1],[0,2],[2,3],[3,4]]
Output: 3

Explanation: The path 0 -> 2 -> 3 -> 4 contains 3 nodes that are colored “a” (red in the above image).

Example 2:

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RI8Gsdor-1681017337782)(null)]

Input: colors = “a”, edges = [[0,0]]
Output: -1

Explanation: There is a cycle from 0 to 0.

Constraints:

• n == colors.length
• m == edges.length
• 1 <= n <= 10^5
• 0 <= m <= 10^5
• colors consists of lowercase English letters.
• 0 <= aj, bj < n

---

提示基本把解这题的关键点都说清楚了， 按提示中的方式来写即可

---

impl Solution {
    pub fn largest_path_value(colors: String, edges: Vec<Vec<i32>>) -> i32 {
        let colors: Vec<char> = colors.chars().collect();
        let mut counts = vec![vec![0; 26]; colors.len()];
        let mut indegrees = vec![0; colors.len()];
        let edges = edges.into_iter().fold(vec![Vec::new(); colors.len()], |mut l, e| {
            indegrees[e[1] as usize] += 1;
            counts[e[0] as usize][colors[e[0] as usize] as usize - 97] = 1;
            counts[e[1] as usize][colors[e[1] as usize] as usize - 97] = 1;
            l[e[0] as usize].push(e[1] as usize);
            l
        });
        let mut queue: Vec<usize> = indegrees.iter().enumerate().filter_map(|(i, &v)| if v == 0 { Some(i as usize) } else { None }).collect();
        let mut ans = 1;
        let mut visited = 0;
        while let Some(n) = queue.pop() {
            visited += 1;
            ans = ans.max(counts[n].iter().map(|v| *v).max().unwrap());
            for &next in &edges[n] {
                for c in 'a'..='z' {
                    counts[next][c as usize - 97] = counts[next][c as usize - 97].max(counts[n][c as usize - 97] + if colors[next] == c { 1 } else { 0 });
                }
                indegrees[next] -= 1;
                if indegrees[next] == 0 {
                    queue.push(next);
                }
            }
        }
        if visited < colors.len() {
            -1
        } else {
            ans
        }
    }
}