LeetCode每日一题(2492. Minimum Score of a Path Between Two Cities)

You are given a positive integer n representing n cities numbered from 1 to n. You are also given a 2D array roads where roads[i] = [ai, bi, distancei] indicates that there is a bidirectional road between cities ai and bi with a distance equal to distancei. The cities graph is not necessarily connected.

The score of a path between two cities is defined as the minimum distance of a road in this path.

Return the minimum possible score of a path between cities 1 and n.

Note:

A path is a sequence of roads between two cities.
It is allowed for a path to contain the same road multiple times, and you can visit cities 1 and n multiple times along the path.
The test cases are generated such that there is at least one path between 1 and n.

Example 1:

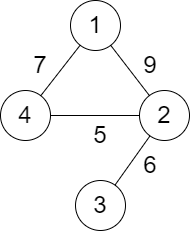
Input: n = 4, roads = [[1,2,9],[2,3,6],[2,4,5],[1,4,7]]
Output: 5

Explanation: The path from city 1 to 4 with the minimum score is: 1 -> 2 -> 4. The score of this path is min(9,5) = 5.
It can be shown that no other path has less score.

Example 2:

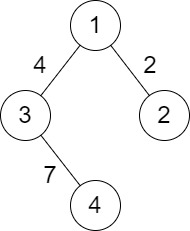
Input: n = 4, roads = [[1,2,2],[1,3,4],[3,4,7]]
Output: 2

Explanation: The path from city 1 to 4 with the minimum score is: 1 -> 2 -> 1 -> 3 -> 4. The score of this path is min(2,2,4,7) = 2.

Constraints:

• 2 <= n <= 10^5
• 1 <= roads.length <= 10^5
• roads[i].length == 3
• 1 <= ai, bi <= n
• ai != bi
• 1 <= distancei <= 10^4
• There are no repeated edges.
• There is at least one path between 1 and n.

---

先说目前的解法， 从 1 开始 bfs 遍历整个与 1 相连的 component, 找出其中所有 path 中 distance 的最小值。

写到这我突然想到， 如果用 union-find 的方法找所有与 1 在同一个 component 中的 node， 找的过程中同时把最小的 distance 找出来，这样也是可以解出来的。可能时间复杂度还会低一点。有兴趣的同学可以实现一下

---

use std::collections::HashMap;

impl Solution {
    pub fn min_score(n: i32, roads: Vec<Vec<i32>>) -> i32 {
        let roads = roads.into_iter().fold(HashMap::new(), |mut m, r| {
            m.entry(r[0] as usize)
                .or_insert(Vec::new())
                .push((r[1] as usize, r[2]));
            m.entry(r[1] as usize)
                .or_insert(Vec::new())
                .push((r[0] as usize, r[2]));
            m
        });
        let mut ans = i32::MAX;
        let mut visited = vec![false; n as usize + 1];
        let mut queue = vec![1];
        visited[1] = true;
        while let Some(p) = queue.pop() {
            for next in roads.get(&p).unwrap() {
                ans = ans.min(next.1);
                if !visited[next.0] {
                    visited[next.0] = true;
                    queue.push(next.0);
                }
            }
        }
        ans
    }
}