LeetCode每日一题(1386. Cinema Seat Allocation)

A cinema has n rows of seats, numbered from 1 to n and there are ten seats in each row, labelled from 1 to 10 as shown in the figure above.

Given the array reservedSeats containing the numbers of seats already reserved, for example, reservedSeats[i] = [3,8] means the seat located in row 3 and labelled with 8 is already reserved.

Return the maximum number of four-person groups you can assign on the cinema seats. A four-person group occupies four adjacent seats in one single row. Seats across an aisle (such as [3,3] and [3,4]) are not considered to be adjacent, but there is an exceptional case on which an aisle split a four-person group, in that case, the aisle split a four-person group in the middle, which means to have two people on each side.

Example 1:

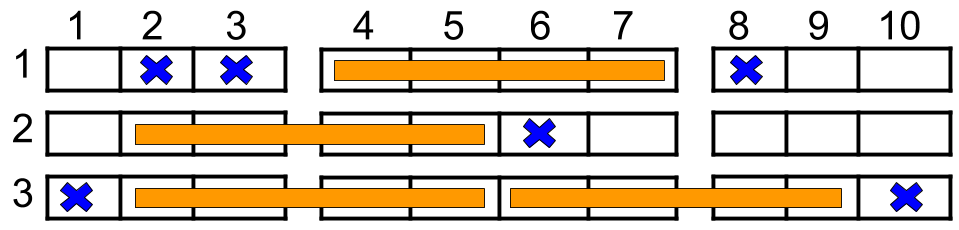
Input: n = 3, reservedSeats = [[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]]
Output: 4

Explanation: The figure above shows the optimal allocation for four groups, where seats mark with blue are already reserved and contiguous seats mark with orange are for one group.

Example 2:

Input: n = 2, reservedSeats = [[2,1],[1,8],[2,6]]
Output: 2

Example 3:

Input: n = 4, reservedSeats = [[4,3],[1,4],[4,6],[1,7]]
Output: 4

Constraints:

• 1 <= n <= 10^9
• 1 <= reservedSeats.length <= min(10*n, 10^4)
• reservedSeats[i].length == 2
• 1 <= reservedSeats[i][0] <= n
• 1 <= reservedSeats[i][1] <= 10
• All reservedSeats[i] are distinct.

---

座位检查比较容易， 因为一共就 4 种模式:

1. [2, 3, 4, 5] + [6, 7, 8, 9]
2. [2, 3, 4, 5]
3. [4, 5, 6, 7]
4. [6, 7, 8, 9]
   按顺序检查， 它们之间是互斥的， 有一种成立，后面的就不必检查了。

但是要注意的是，reserved_seats 中的行不是全部的行， 也就是一些行不会有保留座位， 这些行每行都可以放 2 组

---

impl Solution {
    pub fn max_number_of_families(n: i32, mut reserved_seats: Vec<Vec<i32>>) -> i32 {
        reserved_seats.sort_by_key(|l| (l[0], l[1]));
        let mut seats = 0;
        let mut row = 1;
        let mut ans = 0;
        for reserved in reserved_seats {
            let (r, c) = (reserved[0], reserved[1]);
            if r != row {
                if seats | 0b1000000001 == 0b1000000001 {
                    ans += 2;
                } else if seats | 0b1000011111 == 0b1000011111 {
                    ans += 1
                } else if seats | 0b1110000111 == 0b1110000111 {
                    ans += 1;
                } else if seats | 0b1111100001 == 0b1111100001 {
                    ans += 1;
                }
                ans += (r - row - 1) * 2;
                seats = 0;
                row = r;
            }
            seats |= 1 << (c - 1);
        }
        if seats | 0b1000000001 == 0b1000000001 {
            ans += 2;
        } else if seats | 0b1000011111 == 0b1000011111 {
            ans += 1
        } else if seats | 0b1110000111 == 0b1110000111 {
            ans += 1;
        } else if seats | 0b1111100001 == 0b1111100001 {
            ans += 1;
        }
        ans += (n - row) * 2;
        ans
    }
}