LeetCode每日一题(2421. Number of Good Paths)

There is a tree (i.e. a connected, undirected graph with no cycles) consisting of n nodes numbered from 0 to n - 1 and exactly n - 1 edges.

You are given a 0-indexed integer array vals of length n where vals[i] denotes the value of the ith node. You are also given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting nodes ai and bi.

A good path is a simple path that satisfies the following conditions:

The starting node and the ending node have the same value.
All nodes between the starting node and the ending node have values less than or equal to the starting node (i.e. the starting node’s value should be the maximum value along the path).
Return the number of distinct good paths.

Note that a path and its reverse are counted as the same path. For example, 0 -> 1 is considered to be the same as 1 -> 0. A single node is also considered as a valid path.

Example 1:

Input: vals = [1,3,2,1,3], edges = [[0,1],[0,2],[2,3],[2,4]]
Output: 6

Explanation: There are 5 good paths consisting of a single node.
There is 1 additional good path: 1 -> 0 -> 2 -> 4.
(The reverse path 4 -> 2 -> 0 -> 1 is treated as the same as 1 -> 0 -> 2 -> 4.)
Note that 0 -> 2 -> 3 is not a good path because vals[2] > vals[0].

Example 2:

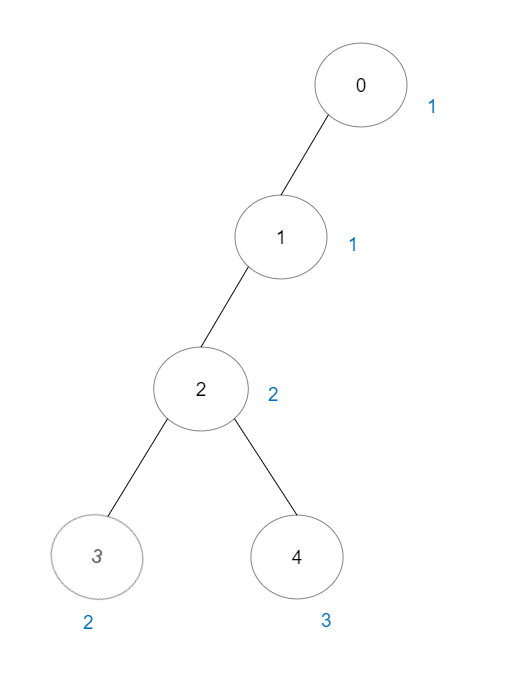
Input: vals = [1,1,2,2,3], edges = [[0,1],[1,2],[2,3],[2,4]]
Output: 7

Explanation: There are 5 good paths consisting of a single node.
There are 2 additional good paths: 0 -> 1 and 2 -> 3.

Example 3:

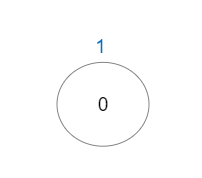
Input: vals = [1], edges = []
Output: 1

Explanation: The tree consists of only one node, so there is one good path.

Constraints:

• n == vals.length
• 1 <= n <= 3 * 104
• 0 <= vals[i] <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• edges represents a valid tree.

---

感觉好难, 不过收获也不少。

我们将 nodes 根据 value 进行分组， 相同 value 的 nodes 放到同一个组中， 然后我们再按照 value 从小到大的来处理这些 groups。我们每次把 group 中的 nodes 放到当前的 graph 中， 这些 nodes 要么与原有的 graph 中的 components 有连接， 要么没有连接, 没有连接的 node 自己成为 graph 中的一个 component， 因为我们是按照 value 从小到大的顺序来往里面添加这些 nodes 的， 所以在任何时间点， graph 中已有的任何一个 node 的 value 一定是小于当前要添加进去的 node 的 value 的。也就是说，当前 group 中的任意 2 个 node, 只要他们两个添加进 graph 后处于同一个 component， 那这 2 个 node 之间一定是存在一条 good path 的。 我们用 union find 来处理这些 components 的连接和合并。nodes 之间只要有相同的 parent， 我们就可以判定有 good path 的存在。最后一个问题是，如果一个 component 中有 n 个值相同的节点， 那这 n 个节点会组成多少 good path 呢?假设 a、b、c 三个节点具有相同值且处于同一 component 中， 我们先从 a 开始统计， [a, a->b, a->c], 然后统计 b, b, [b, b->c], 然后统计 c, [c], 一共是 3 + 2 + 1 = 6 个 good path。这不难看出， 如果有 n 个节点， 那 good path 的数量应该是, n + (n-1) + (n-2) + … + (n - (n-2)) + (n - (n - 1)) = n * n - n * (n - 1) / 2 = n * ( n - (n - 1) / 2) = n * (2n - n + 1) / 2 = n * (n + 1) / 2

---

use std::collections::HashMap;

impl Solution {
    fn find(parents: &mut Vec<i32>, target: i32) -> i32 {
        if parents[target as usize] == target {
            return target;
        }
        let p = Solution::find(parents, parents[target as usize]);
        parents[target as usize] = p;
        p
    }

    fn union(parents: &mut Vec<i32>, vals: &Vec<i32>, a: i32, b: i32) {
        let parent_a = Solution::find(parents, a);
        let parent_b = Solution::find(parents, b);
        if vals[parent_a as usize] < vals[parent_b as usize] {
            parents[parent_b as usize] = parent_a;
            return;
        }
        parents[parent_a as usize] = parent_b;
    }

    pub fn number_of_good_paths(vals: Vec<i32>, edges: Vec<Vec<i32>>) -> i32 {
        let mut vals_to_nodes: Vec<(i32, Vec<i32>)> = vals
            .iter()
            .enumerate()
            .fold(HashMap::new(), |mut m, (i, v)| {
                m.entry(v).or_insert(vec![]).push(i as i32);
                m
            })
            .into_iter()
            .map(|(&val, nodes)| (val, nodes))
            .collect();
        vals_to_nodes.sort();
        let mut conns = vec![vec![]; vals.len()];
        for e in &edges {
            conns[e[0] as usize].push(e[1]);
            conns[e[1] as usize].push(e[0]);
        }
        let mut parents = (0..vals.len() as i32).collect();
        let mut ans = 0;
        for (_, nodes) in vals_to_nodes {
            let mut groups = HashMap::new();
            for &node in &nodes {
                for &conn in &conns[node as usize] {
                    if vals[conn as usize] > vals[node as usize] {
                        continue;
                    }
                    Solution::union(&mut parents, &vals, node, conn);
                }
            }
            for &node in &nodes {
                let parent = Solution::find(&mut parents, node);
                *groups.entry(parent).or_insert(0) += 1;
            }
            for &n in groups.values() {
                ans += n * (n + 1) / 2;
            }
        }
        ans
    }
}