LeetCode每日一题(1659. Maximize Grid Happiness)

You are given four integers, m, n, introvertsCount, and extrovertsCount. You have an m x n grid, and there are two types of people: introverts and extroverts. There are introvertsCount introverts and extrovertsCount extroverts.

You should decide how many people you want to live in the grid and assign each of them one grid cell. Note that you do not have to have all the people living in the grid.

The happiness of each person is calculated as follows:

Introverts start with 120 happiness and lose 30 happiness for each neighbor (introvert or extrovert).
Extroverts start with 40 happiness and gain 20 happiness for each neighbor (introvert or extrovert).
Neighbors live in the directly adjacent cells north, east, south, and west of a person’s cell.

The grid happiness is the sum of each person’s happiness. Return the maximum possible grid happiness.

Example 1:

Input: m = 2, n = 3, introvertsCount = 1, extrovertsCount = 2
Output: 240

Explanation: Assume the grid is 1-indexed with coordinates (row, column).
We can put the introvert in cell (1,1) and put the extroverts in cells (1,3) and (2,3).

• Introvert at (1,1) happiness: 120 (starting happiness) - (0 * 30) (0 neighbors) = 120
• Extrovert at (1,3) happiness: 40 (starting happiness) + (1 * 20) (1 neighbor) = 60
• Extrovert at (2,3) happiness: 40 (starting happiness) + (1 * 20) (1 neighbor) = 60
  The grid happiness is 120 + 60 + 60 = 240.
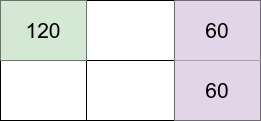
  The above figure shows the grid in this example with each person’s happiness. The introvert stays in the light green cell while the extroverts live on the light purple cells.

Example 2:

Input: m = 3, n = 1, introvertsCount = 2, extrovertsCount = 1
Output: 260

Explanation: Place the two introverts in (1,1) and (3,1) and the extrovert at (2,1).

• Introvert at (1,1) happiness: 120 (starting happiness) - (1 * 30) (1 neighbor) = 90
• Extrovert at (2,1) happiness: 40 (starting happiness) + (2 * 20) (2 neighbors) = 80
• Introvert at (3,1) happiness: 120 (starting happiness) - (1 * 30) (1 neighbor) = 90
  The grid happiness is 90 + 80 + 90 = 260.

Example 3:

Input: m = 2, n = 2, introvertsCount = 4, extrovertsCount = 0
Output: 240

Constraints:

• 1 <= m, n <= 5
• 0 <= introvertsCount, extrovertsCount <= min(m * n, 6)

---

假设我们以从上向下从左到右的顺序来填充整个 grid， 那我们可以得出以下几个结论:

1. 每个格子我们可以填充内向的人、外向的人或者什么都不填
2. 当我们填充内向的人或者外向的人的时候， 受影响的只有当前格子的左侧的格子和上方的格子, 因为右方和下方还没有被填充
3. 能影响后面结果的其实只有最后填充的那 n 个格子， 因为这些格子的下方或者右方存在未填充的格子

这样我们大致的思路就有了:

dp(row, col, introvertsCount, extrovertsCount, last_n_stat) =
max(
	introvert_profit + dp(row, col + 1, introvertCount - 1, extrovertCount, last_n_stat.pop_left().push('introvert')),
	extrovert_profit + dp(row, col + 1, introvertCount, extrovertCount -1, last_n_stat.pop_left().push('extrovert')),
	dp(row, col + 1, introvertCount, extrovertCount, last_n_stat.pop_left().push('empty'))

)

我们分开来看

introvert_profit + dp(row, col + 1, introvertCount - 1, extrovertCount, last_n_stat.pop_left().push(‘introvert’))是当前位置插入内向的人的情况, 其中 introvert_profit 是指当前位置插入内向的人对整体快乐度造成的影响，其实就是对左侧和上方的格子造成的影响加上内向者的基本快乐值 120, 后面的 dp 是当前位置插入内向者后，剩余格子所能达到的最大快乐值， 其中 last_n_stat 需要将最左侧的剔除， 然后在末尾添加上当前格子的状态， 剔除的最左侧元素其实就是当前格子上方的格子的填充状态。

外向的和空置的情况跟内向的大同小异， 就不展开说了。

但是实现的时候其实还是有难点的， 首先我们如果不加 memoization， 结果一定是超时。加上的话，我们需要有一个高效的形式来保存 last_n_stat, 我在这些用了两个 mask 来分别保存最后的 n 个格子的内向者和外向者的分布情况。至于 row 和 col 则使用一个 index 来替代， row = index / n, col = index % n

---

use std::collections::HashMap;

impl Solution {
    fn calc_diff(n: usize, idx: usize, i_mask: i32, e_mask: i32, curr: char) -> i32 {
        let row = idx / n;
        let col = idx % n;
        let mut diff = if curr == 'i' { 120 } else { 40 };
        if row > 0 {
		// 当前位置插入内向者
            if curr == 'i' {
		// 上方是内向者
                diff -= ((i_mask >> (n - 1)) & 1) * 60;
		// 上方是外向者
                diff -= ((e_mask >> (n - 1)) & 1) * 10;
            } else {  // 当前位置插入外向者
		// 上方是内向者
                diff -= ((i_mask >> (n - 1)) & 1) * 10;
		// 上方是外向者
                diff += ((e_mask >> (n - 1)) & 1) * 40;
            }
        }
        if col > 0 {
		// 当前位置插入内向者
            if curr == 'i' {
		// 左侧是内向者
                diff -= (i_mask & 1) * 60;
		// 左侧是外向者
                diff -= (e_mask & 1) * 10;
            } else {  // 当前位置插入外向者
		// 左侧是内向者
                diff -= (i_mask & 1) * 10;
		// 左侧是外向者
                diff += (e_mask & 1) * 40;
            }
        }
        diff
    }
    fn dp(m: usize, n: usize, idx: usize, i_count: i32, e_count: i32, i_mask: i32, e_mask: i32, cache: &mut HashMap<(usize, i32, i32, i32, i32), i32>) -> i32 {
        if idx == m * n || i_count == 0 && e_count == 0 {
            return 0;
        }
        let next_i_mask = (i_mask << 1) & 63;
        let next_e_mask = (e_mask << 1) & 63;
        let mut ans = 0;
        if i_count > 0 {
            let diff = Solution::calc_diff(n, idx, i_mask, e_mask, 'i');
            let next = if let Some(c) = cache.get(&(idx + 1, i_count - 1, e_count, next_i_mask | 1, e_mask)) {
                *c
            } else {
                Solution::dp(m, n, idx + 1, i_count - 1, e_count, next_i_mask | 1, next_e_mask, cache)
            };
            ans = ans.max(diff + next);
        }
        if e_count > 0 {
            let diff = Solution::calc_diff(n, idx, i_mask, e_mask, 'e');
            let next = if let Some(c) = cache.get(&(idx + 1, i_count, e_count - 1, next_i_mask, next_e_mask | 1)) {
                *c
            } else {
                Solution::dp(m, n, idx + 1, i_count, e_count - 1, next_i_mask, next_e_mask | 1, cache)
            };
            ans = ans.max(diff + next);
        }
        let next = if let Some(c) = cache.get(&(idx + 1, i_count, e_count, next_i_mask, next_e_mask)) {
            *c
        } else {
            Solution::dp(m, n, idx + 1, i_count, e_count, next_i_mask, next_e_mask, cache)
        };
        ans = ans.max(next);
        cache.insert((idx, i_count, e_count, i_mask, e_mask), ans);
        ans
    }
    pub fn get_max_grid_happiness(m: i32, n: i32, introverts_count: i32, extroverts_count: i32) -> i32 {
        Solution::dp(m as usize, n as usize, 0, introverts_count, extroverts_count, 0, 0, &mut HashMap::new())
    }
}