LeetCode每日一题(240. Search a 2D Matrix II)-优快云博客

本文链接：https://blog.youkuaiyun.com/wangjun861205/article/details/124444566

本文介绍了一种高效的算法，用于在给定的有序矩阵中查找特定目标值。通过利用行和列的递增特性，从右上角开始缩小搜索范围，直至找到目标或搜索边界。适用于解决LeetCode中的搜索网格问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:

Integers in each row are sorted in ascending from left to right.
Integers in each column are sorted in ascending from top to bottom.

Example 1:

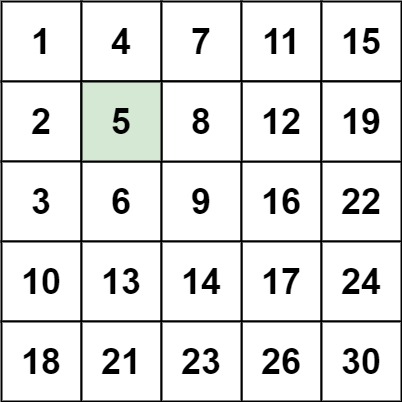
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true

Example 2:

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sHEyRiDc-1651025730748)(https://assets.leetcode.com/uploads/2020/11/24/searchgrid.jpg)]

Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false

Constraints:

m == matrix.length
n == matrix[i].length
1 <= n, m <= 300
-109 <= matrix[i][j] <= 109
All the integers in each row are sorted in ascending order.
All the integers in each column are sorted in ascending order.
-109 <= target <= 109

从最右上角的元素开始，如果目标值小于当前值则可以排除当前列，因为列是递增的，如果目标值大于当前值则可以排除当前行，因为行也是递增的, 这样循环查找，直到找到目标值或者行和列的 index 超出矩阵范围


impl Solution {
    pub fn search_matrix(matrix: Vec<Vec<i32>>, target: i32) -> bool {
        let mut row = 0 as i32;
        let mut col = matrix[0].len() as i32 - 1;
        while row < matrix.len() as i32 && col >= 0 {
            let val = matrix[row as usize][col as usize];
            if val == target {
                return true;
            }
            if val > target {
                col -= 1;
            }
            if val < target {
                row += 1;
            }
        }
        false
    }
}