LeetCode刷题day21||530.二叉搜索树的最小绝对差&&501.二叉搜索树中的众数&&236. 二叉树的最近公共祖先--二叉树

530.二叉搜索树的最小绝对差

题目描述

题目链接

思路分析

• 二叉搜索树，二叉搜索树可是有序的。
  • 1最直观的想法，就是把二叉搜索树转换成有序数组，然后遍历一遍数组，就统计出来最小差值了。
  • 2用一个pre节点记录一下cur节点的前一个节点。

代码

class Solution {
private:
    vector<int> vec;
    void traversal(TreeNode* root) {
        if (root == NULL) return;
        traversal(root->left);
        vec.push_back(root->val);
        traversal(root->right);
    }
public:
    int getMinimumDifference(TreeNode* root) {
        vec.clear();
        traversal(root);
        if (vec.size() < 2) return 0;
        int maxValue = INT_MAX;
        for (int i = 1; i < vec.size(); ++i) {
            maxValue = min(maxValue, vec[i] - vec[i - 1]);
        }
        return maxValue;
    }
};

class Solution {
private:
    int result = INT_MAX;
    TreeNode* pre = NULL;
    void traversal(TreeNode* root) {
        if (root == NULL) return;
        traversal(root->left);
        if (pre) {
            result = min(result, root->val - pre->val);
        }
        pre = root;
        traversal(root->right);
    }
public:
    int getMinimumDifference(TreeNode* root) {
        traversal(root);
        return result;
    }
};

501.二叉搜索树中的众数

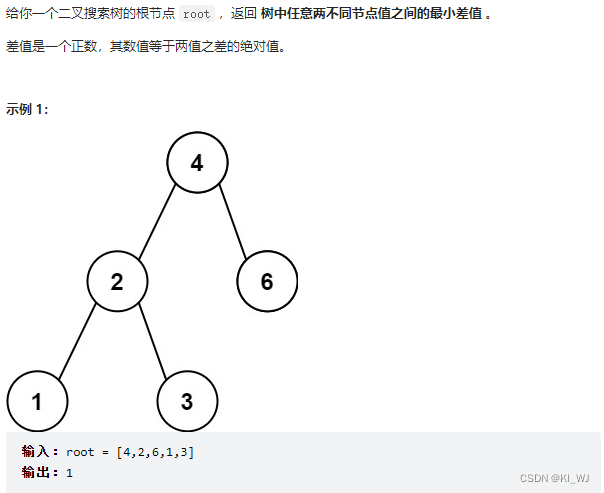
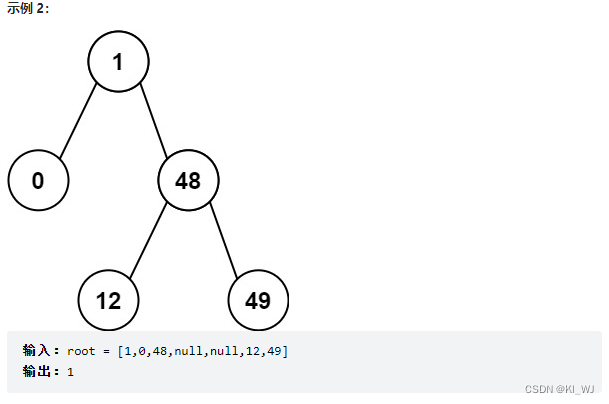
题目描述

题目链接

思路分析

• 如果不是二叉搜索树，最直观的方法一定是把这个树都遍历了，用map统计频率，把频率排个序，最后取前面高频的元素的集合。

代码

class Solution {
private:
    void searchBST(TreeNode* root, unordered_map<int, int>& map) {
        if (root == NULL) return;
        map[root->val]++;
        searchBST(root->left, map);
        searchBST(root->right, map);
    }
    bool static cmp(const pair<int, int>& a, const pair<int, int>& b) {
        return a.second > b.second;
    }
public:
    vector<int> findMode(TreeNode* root) {
        unordered_map<int, int> map;
        vector<int> result;
        if (root == NULL) return result;
        searchBST(root, map);
        vector<pair<int, int>> vec(map.begin(), map.end());
        sort(vec.begin(), vec.end(), cmp);
        result.push_back(vec[0].first);
        for (int i = 1; i < vec.size(); i++) {
            if (vec[i].second == vec[0].second) result.push_back(vec[i].first);
            else break;
        }
        return result;
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    int count = 0;
    int maxCount = 0;
    vector<int> result;
    TreeNode* pre = NULL;
    void searchBST(TreeNode* root) {
        if (root == NULL) return;
        searchBST(root->left);
        if (pre == NULL) {
            count = 1;
        }else if (pre->val == root->val) {
            count++;
        }else {
            count = 1;
        }
        pre = root;
        if (count == maxCount) {
            result.push_back(root->val);
        }
        if (count > maxCount) {
            maxCount = count;
            result.clear();
            result.push_back(root->val);
        }
        searchBST(root->right);
        return;
    }
public:
    vector<int> findMode(TreeNode* root) {
        count = 0;
        maxCount = 0;
        result.clear();
        searchBST(root);
        return result;
    }
};

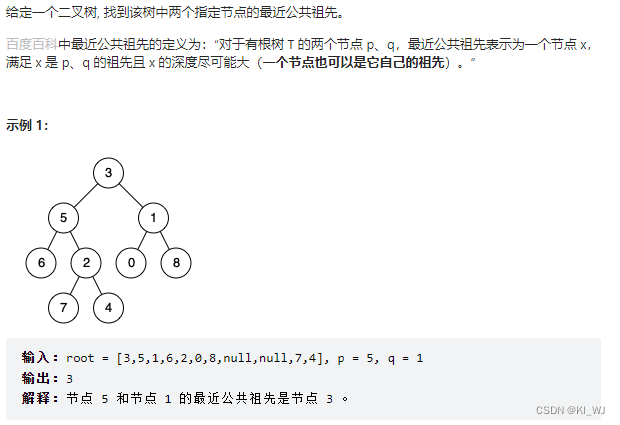
236. 二叉树的最近公共祖先

题目描述

题目链接

思路分析

1. 如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者 左子树出现结点q，右子树出现节点p，那么该节点就是节点p和q的最近公共祖先
   

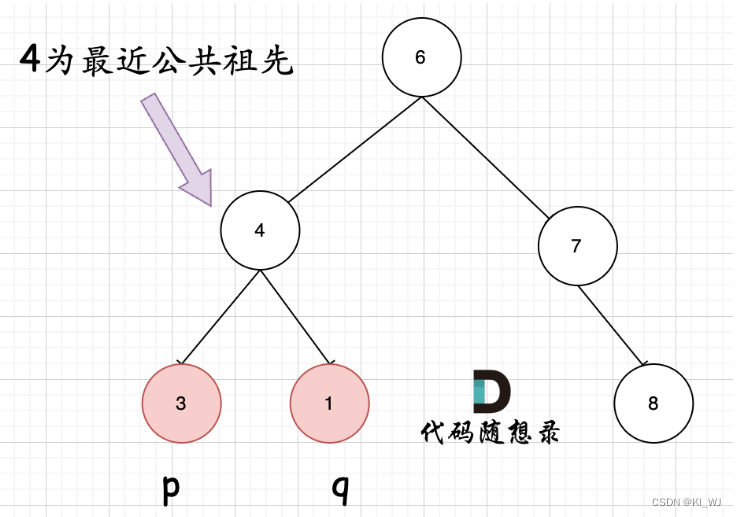
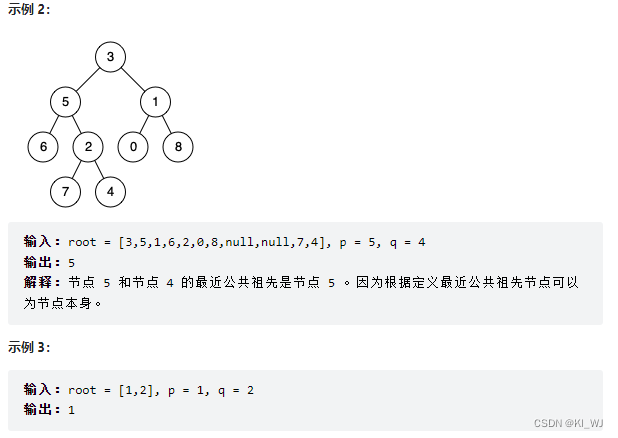
2. 节点本身p(q)，它拥有一个子孙节点q§
   

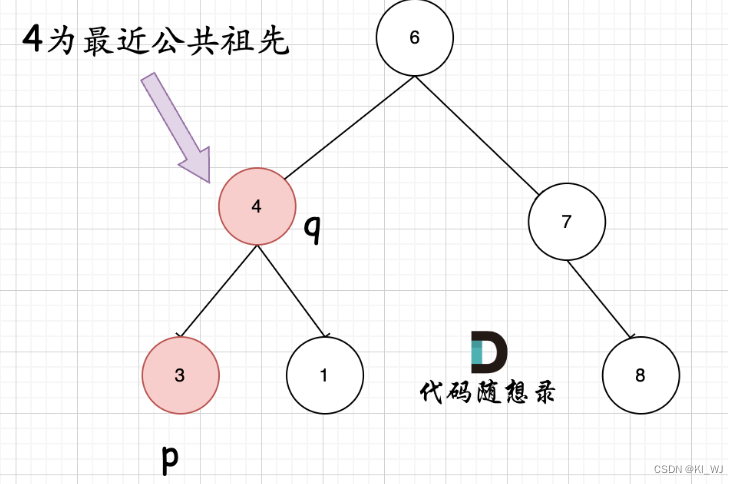
情况一 和 情况二 代码实现过程都是一样的，也可以说，实现情况一的逻辑，顺便包含了情况二。

因为遇到 q 或者 p 就返回，这样也包含了 q 或者 p 本省就是 公共祖先的情况。

代码

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == q || root == p || root == NULL) return root;
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        if (left != NULL && right != NULL) return root;
        else if (left == NULL && right != NULL) return right;
        else if (left != NULL && right == NULL) return left;
        else return NULL;
        
    }
};

精简代码

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == q || root == p || root == NULL) return root;
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        if (left != NULL && right != NULL) return root;
        if (left == NULL) return right;
        return left;
    }
};