stress majorization的推导

最新推荐文章于 2023-01-01 22:43:42 发布

wangjian8006

最新推荐文章于 2023-01-01 22:43:42 发布

阅读量1.6k

点赞数

分类专栏： C 文章标签：算法

C 专栏收录该内容

141 篇文章

订阅专栏

本文介绍了一种基于弹簧模型的二维图布局算法，通过将图中的边视为弹簧，利用能量最小化原理确定节点的最佳位置。文章详细解释了算法背后的数学原理，并提供了具体的计算公式。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

我们将一个二维图看成一个动能系统，其中每两个结点之间有一个作用力，我们可以将这个作用力看成是弹簧的弹力，要使整个动能系统达到动能最小，达到平衡状态.

根据Kamada and Kawai[15]中得到：

$\sigma(X)=\sum_{i<j\le n}w_{ij}(d_{ij}(X)-\delta_{ij})^2$

i<j是因为我们研究的是无向图，不必重复计算。

dij(X)表示结点i与j的欧几里德距离，因为是一张二维图，那么他们在坐标系中，dij(X)表示他们的距离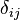， $\delta_{ij}$ 表示i到j的理想距离，我们用图论距离（最短距离）表示。

wij是一个dij的-a次方，a一般取2，表示是一张二维布局的图。

将其按完全平方展开，得到了：

$\sigma(X)=\sum_{i<j\le n}w_{ij}(d_{ij}(X)-\delta_{ij})^2 =\sum_{i<j}w_{ij}\delta_{ij}^2 + \sum_{i<j}w_{ij}d_{ij}^2(X)-2\sum_{i<j}w_{ij}\delta_{ij}d_{ij}(X)$

因为我们要对X的位置进行变换，所以将X看做成一个未知数，那么这个函数的曲面是凹凸不平的，通过计算机，无法得到一个准确的最小值，所以我们将对这个式子进行变换。

对于第一项，都是我们已经可以得到的值，所以将他看成一个常量，不必考虑。

第二项，通过Laplacian系数LW，其实LW是一个n×n的矩阵，可以将其转换为Tr(X‘(LW)X)，X’表示X的倒置，Tr表示矩阵的迹，是主对角线上元素之和。而拉普拉斯系数LW有，当i不等于j时LW=wij，当i等于j时LW=wik之和(i≠k，k=1,2,3...n)。

第三项：

$\sum_{i<j}w_{ij}\delta_{ij}d_{ij}(X)=\,\operatorname{tr}\, X'B(X)X \ge \,\operatorname{tr}\, X'B(Z)Z$

当 $B(Z)$ 为:

$b_{ij}=-\frac{w_{ij}\delta_{ij}}{d_{ij}(Z)}$ for $d_{ij}(Z)\ne 0, i \ne j$

并且 $b_{ij}=0$ for $d_{ij}(Z)=0, i\ne j$

并且 $b_{ii}=-\sum_{j=1,j\ne i}^n b_{ij}$ .

综上所述：

$\sigma(X)=C+\,\operatorname{tr}\, X'VX - 2 \,\operatorname{tr}\, X'B(X)X\le C+\,\operatorname{tr}\, X' V X - 2 \,\operatorname{tr}\, X'B(Z)Z = \tau(X,Z)$

对于其算法，可以由共轭梯度来求解，也可以：

对于第 k^th 步，我们设置 $Z\leftarrow X^{k-1}$

$X^k\leftarrow \min_X \tau(X,Z)$

当 $\sigma(X^{k-1})-\sigma(X^{k})<\epsilon$ 满足结束。∈一般取10的-4次方。

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。