LeetCode第22题：Generate Parentheses（C++）详解

最新推荐文章于 2021-03-09 09:00:14 发布

Mark-Wang

最新推荐文章于 2021-03-09 09:00:14 发布

阅读量305

点赞数

CC 4.0 BY-SA版权

分类专栏： leetcode

本文链接：https://blog.youkuaiyun.com/wanghuan1990519wha/article/details/99707388

leetcode 专栏收录该内容

34 篇文章

订阅专栏

本文深入解析了生成括号组合的经典算法，通过递归方法生成所有合法的括号字符串组合，满足左右括号数量相等且正确配对的条件。提供了C++实现代码，并对比两种不同的递归策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Generate Parentheses
Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.
For example, given n = 3, a solution set is:

[
“((()))”,
“(()())”,
“(())()”,
“()(())”,
“()()()”
]

题目解析：初看之下，不知如何入手，仔细分析，求出所有括号组合，且需要满足如下条件：
1.左右括号数一致；
2.左右括号需配对。

代码：

class Solution {
public:
    vector<string> generateParenthesis(int n) {
        vector<string> res;
        generateParenthesisDFS(n, n, "", res);
        return res;
    }
    
    void generateParenthesisDFS(int left, int right, string out, vector<string> &res) {
        if (left > right) return;
        if (left == 0 && right == 0) res.push_back(out);
        else {
            if (left > 0) generateParenthesisDFS(left - 1, right, out + '(', res);
            if (right > 0) generateParenthesisDFS(left, right - 1, out + ')', res);
        }
    }
};

解析：首先感谢大神得博文，地址如下：
https://www.cnblogs.com/love-yh/p/7159404.html
来说说解法思路：递归
不满足的条件：
1.左括号数大于右括号数：比如"())",出现此情况就可终止递归；
2.剩余括号数为0时，递归终止。
因所有情形，开头字符肯定是’(’，所以递归首先加上’(’；
开始遍历：举个例子
第一个字符’(’; left = 2；right = 3
第二个字符可以是’)‘或’(,‘可得’()‘或者((";left = 2，right = 2；或left = 1，right = 3
第二个字符如果是’)’，第三个字符如果是’)’,此时得到’())’，此种情况，递归就可终止啦。
依次类推，当left和right都为0时，即为满足条件的情形。
DFS算法博文推荐：
https://www.cnblogs.com/OctoptusLian/p/7429645.html

性能：
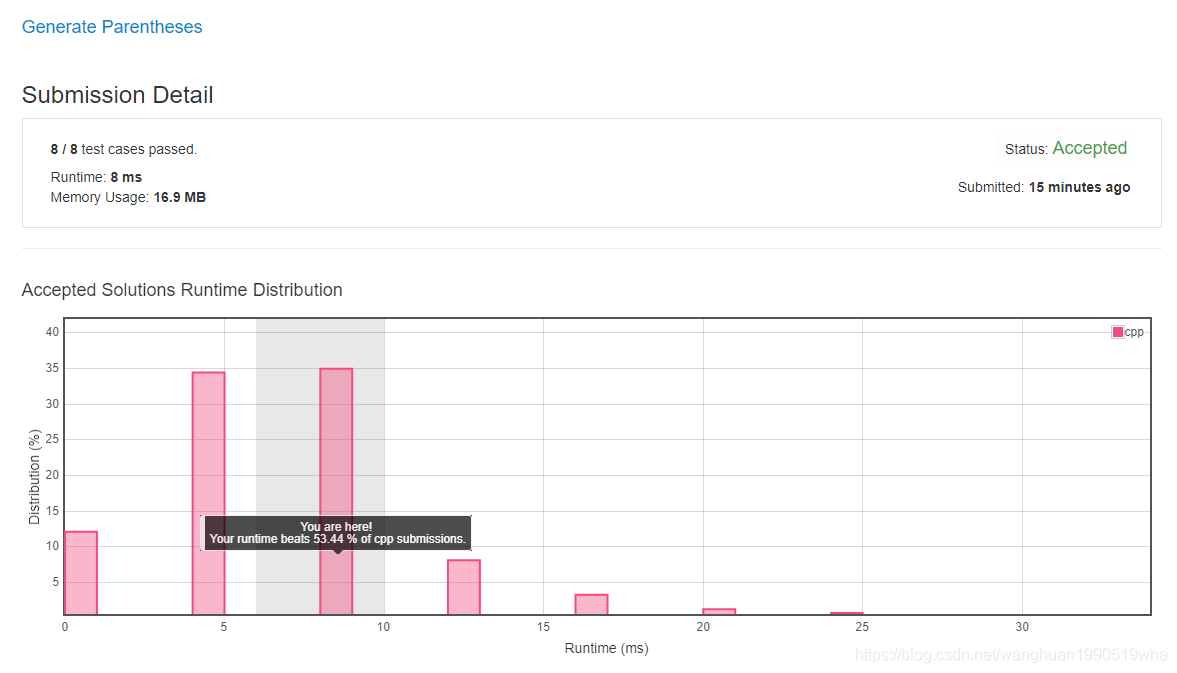
在这里插入图片描述

总结：
此题比较经典，附上大神的解法以及链接，供自己参考学习
https://www.jianshu.com/p/2525612520c6

class Solution {
public:
    vector<string> generateParenthesis(int n) {
        set<string> t;
        if (n == 0) t.insert("");
        else {
            vector<string> pre = generateParenthesis(n - 1);
            for (auto a : pre) {
                for (int i = 0; i < a.size(); ++i) {
                    if (a[i] == '(') {
                        a.insert(a.begin() + i + 1, '(');
                        a.insert(a.begin() + i + 2, ')');
                        t.insert(a);
                        a.erase(a.begin() + i + 1, a.begin() + i + 3);
                    }
                }
                t.insert("()" + a);
            }
        }
        return vector<string>(t.begin(), t.end());
    }
};

此解法一处未理解： t.insert("()" + a);
求解析，共勉，谢谢