深度学习花书 学习笔记（未完结）

补充的笔记，可作为知识点补充

笔记链接：

https://zhuanlan.zhihu.com/p/38431213   

​​​​​​深度学习花书读书笔记目录 - 知乎 (zhihu.com)

第二章：

无论是本征分解，还是奇异值分解，中间的对角矩阵的值就相当于某个相关特征的重要程度，因为对于本征分解，矩阵A实际上是将空间在其本征向量的方向上各自拉伸了对应的本征值的尺度。

第三章：

先给出信息熵的公式：

                                            

其中：𝑝(𝑥𝑖)代表随机事件𝑥𝑖的概率。 

信息的大小跟随机事件的概率有关。越小概率的事情发生了产生的信息量越大，如湖南产生 的地震了；越大概率的事情发生了产生的信息量越小，如太阳从东边升起来了（肯定发生嘛， 没什么信息量）。这很好理解！

因此一个具体事件的信息量应该是随着其发生概率而递减的，且不能为负。但是这个表示信 息量函数的形式怎么找呢？随着概率增大而减少的函数形式太多了！不要着急，我们还有下 面这条性质。

如果我们有俩个不相关的事件 x 和 y，那么我们观察到的俩个事件同时发生时获得的信息应 该等于观察到的事件各自发生时获得的信息之和，即： h(x,y) = h(x) + h(y)

由于 x，y 是俩个不相关的事件，那么满足 p(x,y) = p(x)*p(y).

根据上面推导，我们很容易看出 h(x)一定与 p(x)的对数有关（因为只有对数形式的真数相乘 之后，能够对应对数的相加形式，可以试试）。因此我们有信息量公式如下：

𝐡(𝐱) = −𝒍𝒐𝒈𝟐𝒑(𝒙)

（1）为什么有一个负号？其中，负号是为了确保信息一定是正数或者是 0，总不能为负数吧！

（2）为什么底数为 2 这是因为，我们只需要信息量满足低概率事件 x 对应于高的信息量。那么对数的选择是任意的。我们只是遵循信息论的普遍传统，使用 2 作为对数的底！ 

信息熵 下面正式引出信息熵：信息量度量的是一个具体事件发生了所带来的信息，而熵则是在结果出来之前对可能产生的信息量的期望——考虑该随机变量的所有可能取值，即所有可能发生事件所带来的信息量的期望。

关于kl散度的解释：Kullback-Leibler(KL)散度介绍 - 知乎 (zhihu.com)

交叉熵作为损失函数

假设一个动物照片的数据集中有5种动物，且每张照片中只有一只动物，每张照片的标签都是one-hot编码。

第一张照片是狗的概率为100%，是其他的动物的概率是0；第二张照片是狐狸的概率是100%，是其他动物的概率是0，其余照片同理；因此可以计算下，每张照片的熵都为0。换句话说，以one-hot编码作为标签的每张照片都有100%的确定度，不像别的描述概率的方式：狗的概率为90%，猫的概率为10%。

假设有两个机器学习模型对第一张照片分别作出了预测：Q1和Q2,而第一张照片的真实标签为[1,0,0,0,0]。

两个模型预测效果如何呢，可以分别计算下交叉熵：

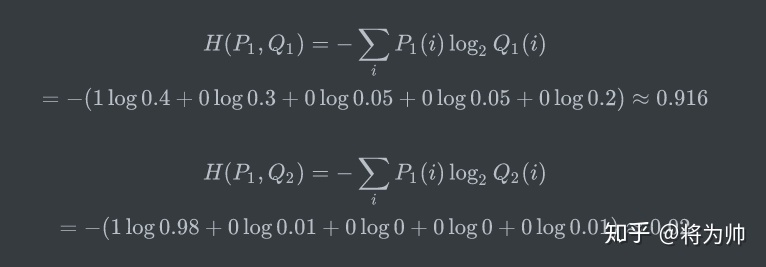
交叉熵对比了模型的预测结果和数据的真实标签，随着预测越来越准确，交叉熵的值越来越小，如果预测完全正确，交叉熵的值就为0。因此，训练分类模型时，可以使用交叉熵作为损失函数。

第五章

正则化：减少测试/泛华误差，防止过拟合（选取中等的入）

最大似然，贝叶斯：减少均方差

最大后验概率估计：防止过拟合

 逻辑回归中的sigmoid函数中，x为特征，θ为权重。