为什么要使用 Bounding-Box 回归 ?
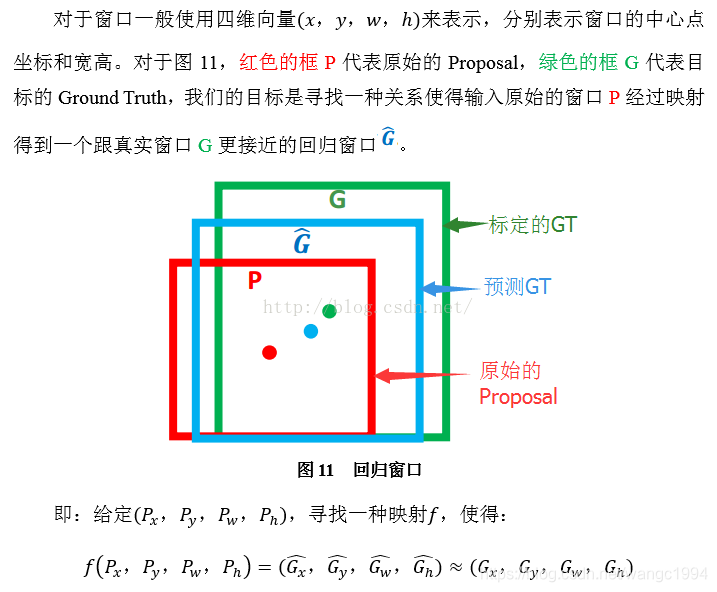
使用 Bounding-Box 回归是 R-CNN 对目标准确定位的关键,能够通过微调的方式减小预测窗口与 Ground Truth 之间的误差。

如上图所示,红色框和绿色框分别表示检测目标的 Region Proposal 和真实的 Ground Truth,红色框虽然把目标识别为飞机,但与绿色框的重合度 IoU < 0.5,这张图还是相当于没有正确检测出飞机,此时就需要使用 Bounding-Box 回归对窗口进行微调,使得经过微调的窗口与 Ground Truth 更接近。
怎么进行微调?
主要就是对 Region Proposal 进行平移和缩放
- 首先平移 (Δx,Δy\Delta x, \Delta yΔx,Δy):Δx=Pwdx(P),Δy=Phdy(P)\Delta x=P_w d_x(P) ,\Delta y = P_h d_y(P)Δx=Pwdx(P),Δy=Phdy(P)
G^x=Px+ΔxG^y=Py+Δy\hat{G}_x = P_x + \Delta x \\ \hat{G}_y = P_y + \Delta yG^x=Px+ΔxG^y=Py+Δy - 后做缩放 (Δw,Δh\Delta w, \Delta hΔw,Δh):Δw=edw(P),Δh=edh(P)\Delta w=e^{d_w(P)},\Delta h=e^{d_h(P)}Δw=edw(P),Δh=edh(P)
G^w=Pw∗ΔwG^h=Ph∗Δh\hat{G}_w = P_w * \Delta w \\ \hat{G}_h = P_h * \Delta hG^w=Pw∗ΔwG^h=Ph∗Δh
转化为一般式表示为:
G^x=Px+Pwdx(P)G^y=Py+Phdy(P)G^w=Pw∗edw(P)G^h=Ph∗edh(P)\hat{G}_x = P_x + P_w d_x(P) \\
\hat{G}_y = P_y + P_h d_y(P) \\
\hat{G}_w = P_w * e^{d_w(P)} \\
\hat{G}_h=P_h * e^{d_h(P)}G^x=Px+Pwdx(P)G^y=Py+Phdy(P)G^w=Pw∗edw(P)G^h=Ph∗edh(P)
由上面的公式可以看出,我们需要学习的是 dx(P),dy(P),dw(P),dh(P)d_x(P),d_y(P),d_w(P),d_h(P)dx(P),dy(P),dw(P),dh(P) 这四个变换,下一步就是设计算法得到这四个映射。当输入的 Region Proposal 与 Ground Truth 相差较小时(R-CNN 设置的是 IoU>0.6),可以认为这种变换是一种线性变换,于是可以使用线性回归来建模对窗口进行微调。
注意:只有当 Region Proposal 和 Ground Truth 比较接近时(线性问题),我们才能将其作为训练样本训练我们的线性回归模型,否则会导致训练的回归模型不work(当Proposal 跟 GT 离得较远,就是复杂的非线性问题了,此时用线性回归建模显然不合理)
构建线性回归模型
输入:Region Proposal,P=(Px,Py,Pw,Ph)P=(P_x, P_y, P_w, P_h)P=(Px,Py,Pw,Ph),但真正的输入是这个窗口对应的 CNN 特征,也就是 R-CNN 结构中 Pool5 层的 features,记为 Φ5\Phi_5Φ5
输出:dx(P),dy(P),dw(P),dh(P)d_x(P),d_y(P),d_w(P),d_h(P)dx(P),dy(P),dw(P),dh(P)
目标函数:d∗(P)=w∗TΦ5(P)d_*(P)=w^T_* \Phi_5(P)d∗(P)=w∗TΦ5(P),w∗w_*w∗ 表示需要学习的参数,d∗(P)d_*(P)d∗(P) 表示预测值
定义 tx=(Gx−Px)Pwty=(Gy−Py)Phtw=logGwPwth=logGhPht_x = \frac{(G_x-P_x)}{P_w}\\
t_y = \frac{(G_y-P_y)}{P_h}\\
t_w=log\frac{G_w}{P_w}\\
t_h=log\frac{G_h}{P_h}tx=Pw(Gx−Px)ty=Ph(Gy−Py)tw=logPwGwth=logPhGh
上面 tx,ty,tw,tht_x, t_y, t_w, t_htx,ty,tw,th 表示从 Region Proposal 到 Ground Truth 真正需要的平移量和缩放量,即目标值。
于是定义损失函数为:
Loss=∑i=1N(t∗i−w^∗TΦ5(Pi))2Loss=\sum^N_{i=1}(t^i_*-\hat{w}_*^T\Phi_5 (P^i))^2Loss=i=1∑N(t∗i−w^∗TΦ5(Pi))2
函数优化目标为:
w∗=argminw^∗∑i=1N(t∗i−w^∗TΦ5(Pi))2+λ∣∣w^∗∣∣2w_*=\underset{\hat{w}_*}{argmin}\sum^N_{i=1}(t^i_*-\hat{w}_*^T\Phi_5 (P^i))^2+\lambda||\hat{w}_*||^2w∗=w^∗argmini=1∑N(t∗i−w^∗TΦ5(Pi))2+λ∣∣w^∗∣∣2
利用梯度下降法就能得到 w∗w_*w∗





 本文深入解析了Bounding-Box回归在R-CNN目标检测算法中的作用及其实现过程。通过微调候选区域,提升检测精度,特别介绍了如何通过线性回归模型进行平移和缩放调整。
本文深入解析了Bounding-Box回归在R-CNN目标检测算法中的作用及其实现过程。通过微调候选区域,提升检测精度,特别介绍了如何通过线性回归模型进行平移和缩放调整。
















 20万+
20万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








