剑指offer-题31：连续子数组的最大和

题目描述

输入一个整型数组，数组里有正数也有负数。数组中一个或连续的多个整数组成一个子数组。求所有子数组的和的最大值。要求时间复杂度为O(n)。

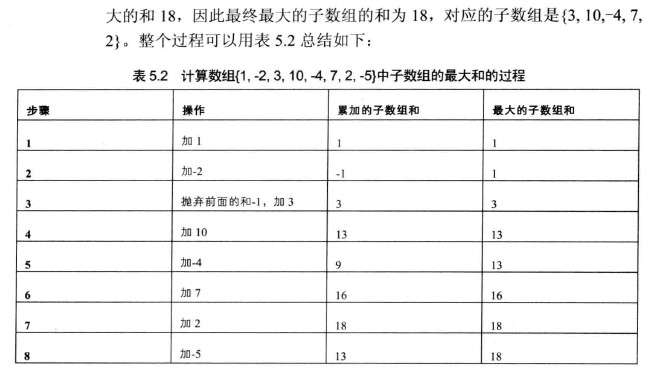
例如：输入数组为{ 1, -2, 3, 10, -4, 7, 2, -5 }，和最大的子数组为{3, 10, -4, 7, 2},因此输出为该子数组的和18。

实验平台：牛客网

---

解决思路：

java:

public class Solution {
    public int FindGreatestSumOfSubArray(int[] array) {
        if (array == null || array.length == 0) {
            return 0;
        } else {
            int curSum = 0;
            int maxSum = 0x80000000; // int类型的最小值
            for (int i = 0; i < array.length; i++) {
                if (curSum <= 0) {
                    curSum = array[i];
                } else {
                    curSum += array[i];
                }
                if (curSum > maxSum) {
                    maxSum = curSum;
                }
            }
            return maxSum;
        }
    }
}

python:

略