从PCA到AutoEncoder

PCA

理论简单，计算只涉及到线性代数的计算，特征保持正交性，如果原始特征不具有正交性，只有独立性，这个时候可以使用ICA。
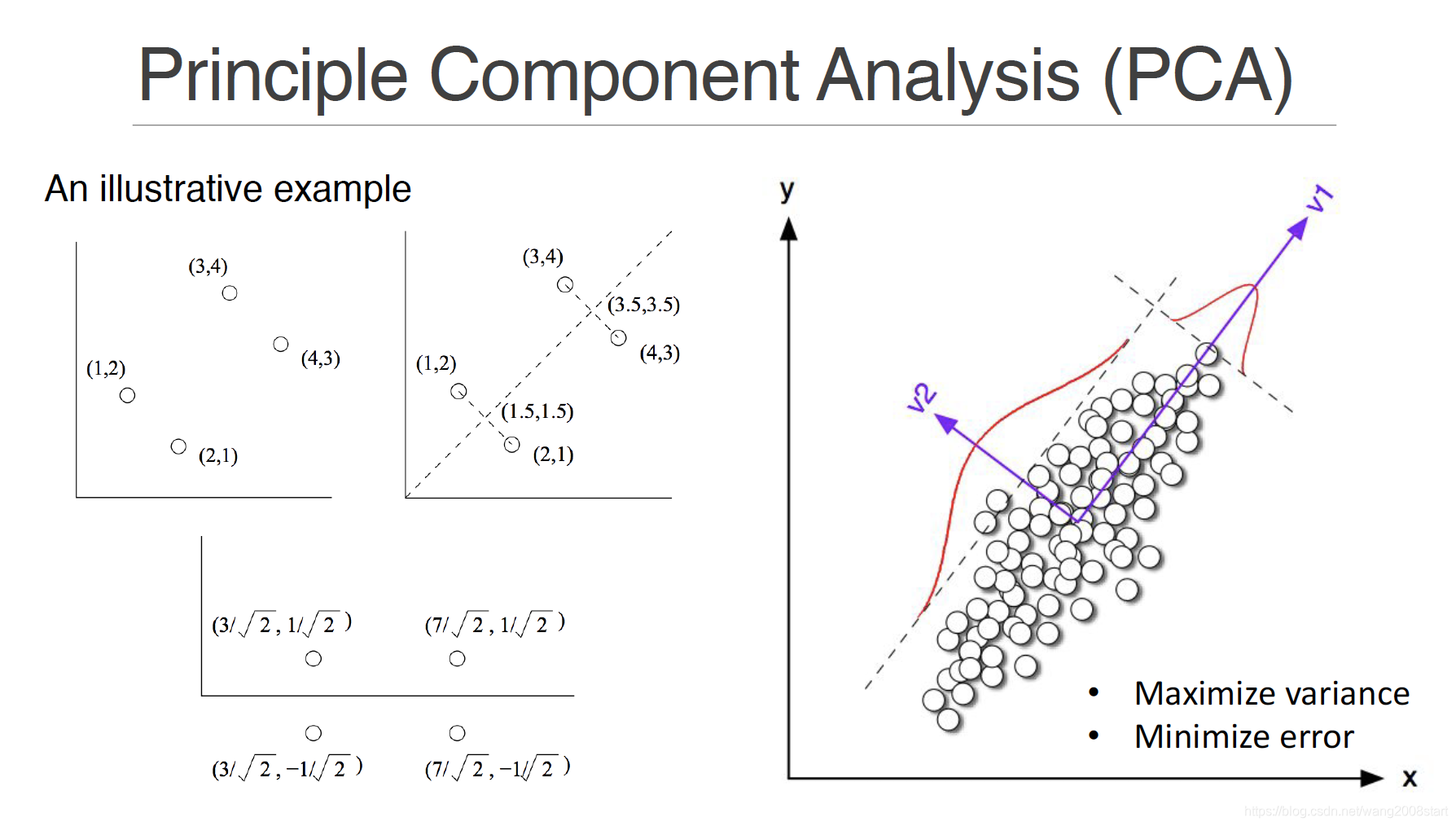
有两种可产生相同算法的等价视角：最大方差和最小重构误差。两种视角都希望找到一组正交投影，把原数据投影到低维的线性子空间上。但最大方差视角是说，我们希望数据投影之后在投影方向上有最大方差；而最小重构误差视角是说，我们希望投影后的数据和原数据之间的均方差最小。
计算过程：

1. 定义样本均值和样本协方差
2. 可以得到某个投影方向u_1上的方差
3. 方差最大作为目标函数，把这个问题看作有约束最优化问题，因此可用拉格朗日乘子法求解，令导数为0，线性代数中的特征值分解问题，求得特征值和特征向量。
   在余下的方向中依次选择最大方差方向，就是S由大到小给出的各个特征值以及对应的特征向量，由于S是实对称矩阵，得到的特征向量之间是正交，线性无关，可以互不影响，依次求解。
   最小重构误差视角和最大方差视角一样，也是特征值问题。只不过这里是去掉较小特征值对应的方向，因为那些方向对应着较小的重构误差，而先前是保留较大特征值对应的方向。但得到的结果是完全一样的。
   
   
   

PCA的复杂度问题，特征分解是 O(n^3) 复杂度，
如果仅需要前M个最大的特征值以及特征向量，那么有一些算法可达到O(M*D^2)复杂度

PPCA

PPCA比起传统PCA，有一点优势就是利用了概率分布。因为我们的数据即使在某个低维子空间上，也不可能分布在整个子空间，而是只处在其中一个小区域。概率模型就很好地利用了这一点。当然，除了生成数据之外，概率模型更大的优势还是通过观察变量，也就是手里的数据，去推断参数也就是$W$、$\mu$、${\sigma }^2$是什么。这就要利用一些统计推断方法，比如最大似然法。但想用最大似然，必须先知道似然函数是什么。
$$x=$$