【Alg_Note】1.1稳定匹配

目录

一、基本概念。

二、G-S算法。

三、有关结论。

四、思考过程。 

---

一、基本概念。

不稳定：一定要两厢情愿。

              e.g.  已匹配( x, * ) , ( *, y)，但是x更喜欢y且y更喜欢x。

稳定：不包含不稳定。

匹配S：

完美匹配：集合中的每个元素（人）都用上了。即一一对应。

                      M中的每个成员和W中的每个成员恰好出现在的一个对中。

优先：m给w的排名高于。

不稳定因素：完美匹配S中存在(m, w)，(, )，m更喜欢且更喜欢m，

                       则(m, )为相对S的不稳定因素。

最佳有效伴侣：

最差有效伴侣：

换而言之

有效伴侣：某个稳定匹配S包含(m, w)，则w是m的有效伴侣。（未必唯一）

最佳伴侣：如果w是m优先级最高的有效伴侣，则w是m的最佳伴侣。（唯一）

二、G-S算法。

G-S算法返回稳定匹配。

对于一般情形，稳定匹配一定存在，可能不唯一，也可能不存在（稳定室友匹配问题）。

Initialize each person to be free.
while (some man is free and has not proposed to every woman)
{
    Choose such a man m.
    w = first woman on man's list to whom m has not yet proposed

    if （w is free）
        assign m and w to be engaged

    else if (w prefers m to m')
        assign m and w to be engaged, and m' to be free

    else
        w rejects m.
}

代码逻辑分析见第四部分。

可以通过对内层循环的女方优先表进行预处理即反向变换，使得后续判别为常数阶代价。

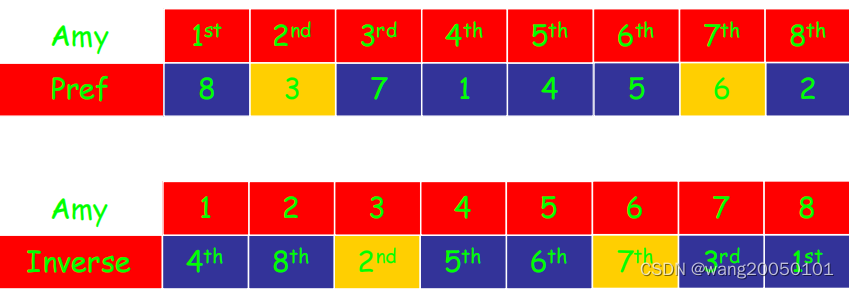
三、有关结论。

 

平衡：尽管m以最佳可能的稳定匹配结束，而w以最差可能的稳定匹配结束，

           但w有主动选择的权利。

四、思考过程。 

假设男女各n人，由男方发出邀请，女方可以选择接受与否。即while中的过程。

while中的过程如下。

1、选定男方m，要求m不处于约会状态且没有向所有女方提出过约会。

2、选定m对应的女方w，要求w是m未提出过约会的女方中m最喜欢的。

3、判断w是否会与m约会：

若w空闲，则约会；

若w与m'正在约会，判断w更喜欢谁；

         若w更喜欢m'，则w与m'继续约会，m空闲；

         若w更喜欢m，则w与m约会，m'空闲。

易得在这个过程中，男方的试图约会对象优先级越来越低，女方相反。

而由于男女人数相等，那么若存在m不在约会状态，那么m一定没有向所有女方提出过约会。

过程中需要考虑如何保存各人的约会状态、优先表等信息。

经梳理可知，需要保存的信息主要有：男女双方各人的优先次序、男女各人的约会状态、男方最后约会对象。合理定义并初始化信息存储后即可按照以上逻辑完成。