符号型数据的 NB 算法

学习来源：日撸 Java 三百行（51-60天，kNN 与 NB）

第 58 天: 符号型数据的 NB 算法

朴素贝叶斯算法（Naive Bayes，NB）是一种是基于贝叶斯定理与特征条件独立假设的分类算法。

数据集
数据集中共有Outlook、Temperature、Humidity、Windy、Play 五个属性，每个属性有多个值，如属性Outlook有Sunny、 Overcast、Rain三个可选取的值。这里我们选用Outlook、Temperature、Humidity、Windy等四个属性作为条件属性。

@relation weather
@attribute Outlook {Sunny, Overcast, Rain}
@attribute Temperature {Hot, Mild, Cool}
@attribute Humidity {High, Normal, Low}
@attribute Windy {FALSE, TRUE}
@attribute Play {N, P}
@data
Sunny,Hot,High,FALSE,N
Sunny,Hot,High,TRUE,N
Overcast,Hot,High,FALSE,P
Rain,Mild,High,FALSE,P
Rain,Cool,Normal,FALSE,P
Rain,Cool,Normal,TRUE,N
Overcast,Cool,Normal,TRUE,P
Sunny,Mild,High,FALSE,N
Sunny,Cool,Normal,FALSE,P
Rain,Mild,Normal,FALSE,P
Sunny,Mild,Normal,TRUE,P
Overcast,Mild,High,TRUE,P
Overcast,Hot,Normal,FALSE,P
Rain,Mild,High,TRUE,N

算法思想
通过某对象的先验概率，利用贝叶斯公式计算出其后验概率，即该对象属于某一类的概率，最后选择具有最大后验概率的类作为该对象所属的类。

独立性假设
令$X=x_1\wedge x_2\wedge x_3\wedge ...\wedge x_m$表示一个条件的组合，如：$Outlook=sunny\wedge Temperature=hot\wedge Humiddity=high\wedge Windy=FALSE$,令$D_i$表示一个事件, 如: $Play=no$. 根据条件概率的式子可知:

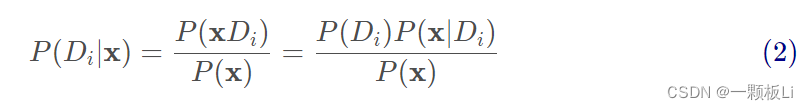
假设各个条件之间是相互独立的，则有：

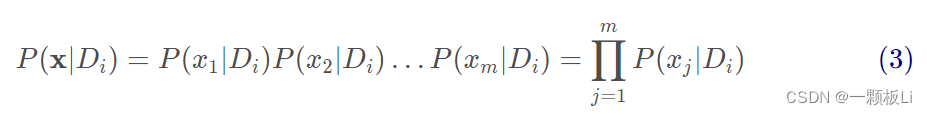
综合 (2)(3) 式可得:


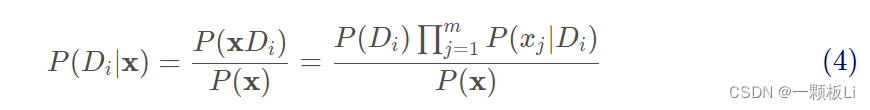
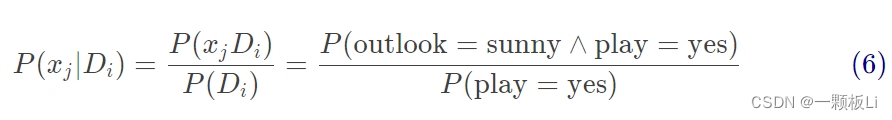
(4)式中的$P(D_i|x)$表示在条件组合x下发生$D_i$的概率。其中分母$P(x)$是计算不了的，但是针对我们分类的目标，在不同类别的分母都一致的情况下，可以只比较分子。因此我们可得出哪个类别的相对概率高, 就可预测为该类的预测方案。即最大后验概率的类别作为该对象所属的类别。预测方案如下所示：

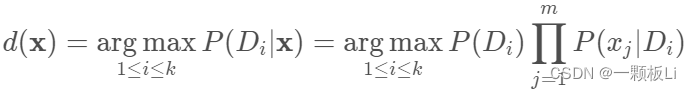
k表示类别数，这里的k为2，因为属性Play只有yes和no两个值；
$argmax$ 表示哪个类别的相对概率高, 我们就预测为该类别。

Laplacian 平滑
在预测方案的连乘因子$P(x_j|D_i)$中, 可能不存在满足$D_i$的情况下发生$x_j$的样本，因此该事件概率可能为0。连乘因子只要有一个为 0, 则乘积一定为 0。因此为了解决该问题, 我们要想办法让这个因子不要取 0 值。

为解决零概率的问题，我们采用Laplacian 平滑的方法:

$P^L(x_j|D_i)=\frac{nP(x_j|D_i)+1}{nP(D_i)+v_j}$

其中，n是样本总数， $v_j$是第j个属性取值的个数。

对于$P(D_i)$也需要进行平滑:

$P^L(D_i)=\frac{nP(D_i)+1}{n+k}$

其中n是样本总数，k是类别数。

Laplacian 平滑的优化目标为:

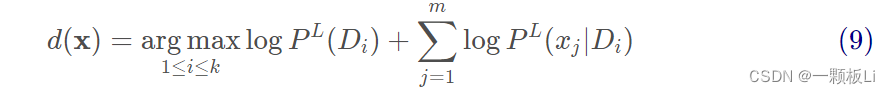
算法步骤：
1.读入weather.arff中的数据。
2.设置数据集类型为符号型。
3.计算类的分布
3.1计算每个类别对应的样本数,即$D_i$的数量，因为Play属性只有no和yes两个值，所以i可取1、2。
3.2计算每个类别的先验概率，即计算每个类别对应的样本数占比,$P(D_i)=D_i/numInstances$，numInstances为总样本数。
3.3根据3.2计算的$P(D_i)$来计算经过 Laplacian 平滑后的类的分布，即$P^L(D_i)$。
4.计算条件概率
4.1计算每个类别的每个属性的每个值所对应的样本数，用三维数组存储。
4.2通过4.1得出的三维数组和3.2得到的类的分布来计算经过 Laplacian 平滑后的条件概率。
5.通过 Laplacian 平滑的优化目标来分类，找到使目标函数最大的$D_i$,则该类别就是待预测对象所属的类别。
6.计算预测准确度。
代码：

package machine_learning;

import java.io.FileReader;
import java.util.Arrays;
import weka.core.*;

/**
 * @Description: The Naive Bayes algorithm.
 * @author: Xin-Yu Li
 * @time: May 8(th),2022
 */
public class NaiveBayes {
	private class GaussianParamters {
		double mu;
		double sigma;

		public GaussianParamters(double paraMu, double paraSigma) {
			mu = paraMu;
			sigma = paraSigma;
		}// Of the constructor

		public String toString() {
			return "(" + mu + ", " + sigma + ")";
		}// Of toString
	}// Of GaussianParamters

	Instances dataset;
	int numClasses;
	int numInstances;
	int numConditions;
	
	int[] predicts;
	double[] classDistribution;
	double[] classDistributionLaplacian;
	double[][][] conditionalCounts;
	double[][][] conditionalProbabilitiesLaplacian;

	GaussianParamters[][] gaussianParameters;

	int dataType;
	public static final int NOMINAL = 0;
	public static final int NUMERICAL = 1;

	public NaiveBayes(String paraFilename) {
		dataset = null;
		try {
			FileReader fileReader = new FileReader(paraFilename);
			dataset = new Instances(fileReader);
			fileReader.close();
		} catch (Exception ee) {
			System.out.println("Cannot read the file: " + paraFilename + "\r\n" + ee);
			System.exit(0);
		} // Of try

		dataset.setClassIndex(dataset.numAttributes() - 1);
		numConditions = dataset.numAttributes() - 1;
		numInstances = dataset.numInstances();
		numClasses = dataset.attribute(numConditions).numValues();
	}// Of the constructor

	public void setDataType(int paraDataType) {
		dataType = paraDataType;
	}// Of setDataType

	public void calculateClassDistribution() {
		classDistribution = new double[numClasses];
		classDistributionLaplacian = new double[numClasses];

		double[] tempCounts = new double[numClasses];
		for (int i = 0; i < numInstances; i++) {
			int tempClassValue = (int) dataset.instance(i).classValue();
			tempCounts[tempClassValue]++;
		} // Of for i

		for (int i = 0; i < numClasses; i++) {
			classDistribution[i] = tempCounts[i] / numInstances;
			classDistributionLaplacian[i] = (tempCounts[i] + 1) / (numInstances + numClasses);
		} // Of for i

		System.out.println("Class distribution: " + Arrays.toString(classDistribution));
		System.out.println("Class distribution Laplacian: " + Arrays.toString(classDistributionLaplacian));
	}// Of calculateClassDistribution

	public void calculateConditionalProbabilities() {
		conditionalCounts = new double[numClasses][numConditions][];
		conditionalProbabilitiesLaplacian = new double[numClasses][numConditions][];

		for (int i = 0; i < numClasses; i++) {
			for (int j = 0; j < numConditions; j++) {
				int tempNumValues = (int) dataset.attribute(j).numValues();
				conditionalCounts[i][j] = new double[tempNumValues];
				conditionalProbabilitiesLaplacian[i][j] = new double[tempNumValues];
			} // Of for j
		} // Of for i

		int[] tempClassCounts = new int[numClasses];
		for (int i = 0; i < numInstances; i++) {
			int tempClass = (int) dataset.instance(i).classValue();
			tempClassCounts[tempClass]++;
			for (int j = 0; j < numConditions; j++) {
				int tempValue = (int) dataset.instance(i).value(j);
				conditionalCounts[tempClass][j][tempValue]++;
			} // Of for j
		} // Of for i

		for (int i = 0; i < numClasses; i++) {
			for (int j = 0; j < numConditions; j++) {
				int tempNumValues = (int) dataset.attribute(j).numValues();
				for (int k = 0; k < tempNumValues; k++) {
					conditionalProbabilitiesLaplacian[i][j][k] = (conditionalCounts[i][j][k] + 1)/ (tempClassCounts[i] + tempNumValues);
				} // Of for k
			} // Of for j
		} // Of for i

		System.out.println("Conditional probabilities: " + Arrays.deepToString(conditionalCounts));
	}// Of calculateConditionalProbabilities

	public void classify() {
		predicts = new int[numInstances];
		for (int i = 0; i < numInstances; i++) {
			predicts[i] = classify(dataset.instance(i));
		} // Of for i
	}// Of classify

	public int classify(Instance paraInstance) {
		if (dataType == NOMINAL) {
			return classifyNominal(paraInstance);
		} 
		else
			return -1;
	}// Of classify

	public int classifyNominal(Instance paraInstance) {
		double tempBiggest = -10000;
		int resultBestIndex = 0;
		for (int i = 0; i < numClasses; i++) {
			double tempClassProbabilityLaplacian = Math.log(classDistributionLaplacian[i]);
			double tempPseudoProbability = tempClassProbabilityLaplacian;
			for (int j = 0; j < numConditions; j++) {
				int tempAttributeValue = (int) paraInstance.value(j);

				tempPseudoProbability += Math.log(conditionalCounts[i][j][tempAttributeValue])- tempClassProbabilityLaplacian;
			} // Of for j

			if (tempBiggest < tempPseudoProbability) {
				tempBiggest = tempPseudoProbability;
				resultBestIndex = i;
			} // Of if
		} // Of for i

		return resultBestIndex;
	}// Of classifyNominal
	
	public double computeAccuracy() {
		double tempCorrect = 0;
		for (int i = 0; i < numInstances; i++) {
			if (predicts[i] == (int) dataset.instance(i).classValue()) {
				tempCorrect++;
			} // Of if
		} // Of for i

		double resultAccuracy = tempCorrect / numInstances;
		return resultAccuracy;
	}// Of computeAccuracy

	public static void testNominal() {
		System.out.println("Hello, Naive Bayes. I only want to test the nominal data.");
		String tempFilename = "C:\\Users\\LXY\\Desktop\\weather.arff";

		NaiveBayes tempLearner = new NaiveBayes(tempFilename);
		tempLearner.setDataType(NOMINAL);
		tempLearner.calculateClassDistribution();
		tempLearner.calculateConditionalProbabilities();
		tempLearner.classify();

		System.out.println("The accuracy is: " + tempLearner.computeAccuracy());
	}// Of testNominal

	public static void main(String[] args) {
		testNominal();
	}// Of main
}// Of class NaiveBayes

运行截图：