算法提高课 -- 7

已于 2024-07-15 23:00:39 修改
阅读量250 收藏 3
点赞数 5
文章标签： 算法 深度优先 图论
于 2024-07-13 19:34:29 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/w532648/article/details/140398629
版权

树型DP

1072.树的最长路径

题目解析：很经典的求树的直径的问题，具体分析以及做法讲解如下图所示：

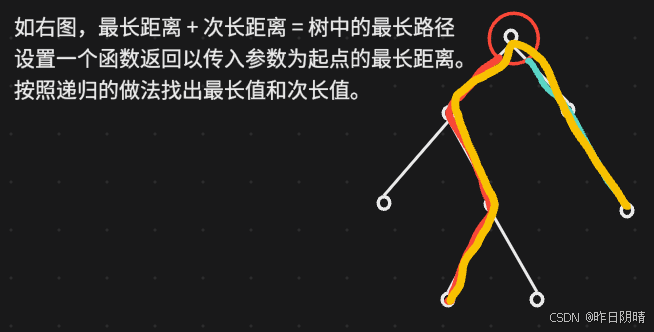
代码 + 注释：

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 10010, M = 2 * N;
int n, e[M], ne[M], w[M], h[N], idx;
int res;
void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
int dfs(int root, int father) { // 参数传入的是根节点和该节点的父节点
    int d1 = 0, d2 = 0; // d1 表示最长距离 d2 表示次长距离
    for (int i = h[root]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == father) continue;
        int d = dfs(j, root) + w[i];
        if (d >= d1) d2 = d1, d1 = d;
        else if (d > d2) d2 = d;
    }
    res = max(res, d1 + d2);
    return d1; // 返回的是以root为起点的最长距离
}
int main() {
    scanf("%d", &n);
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i++) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }
    dfs(1, -1);
    printf("%d\n", res);
    return 0;
}

1073.树的中心

解题思路：和上一题不同的是，我们不仅需要记录下最长和次长值，还需要记录一个从该节点往上蔓延的路线长度；同时还需要记录最长路径的数组，原因如下：

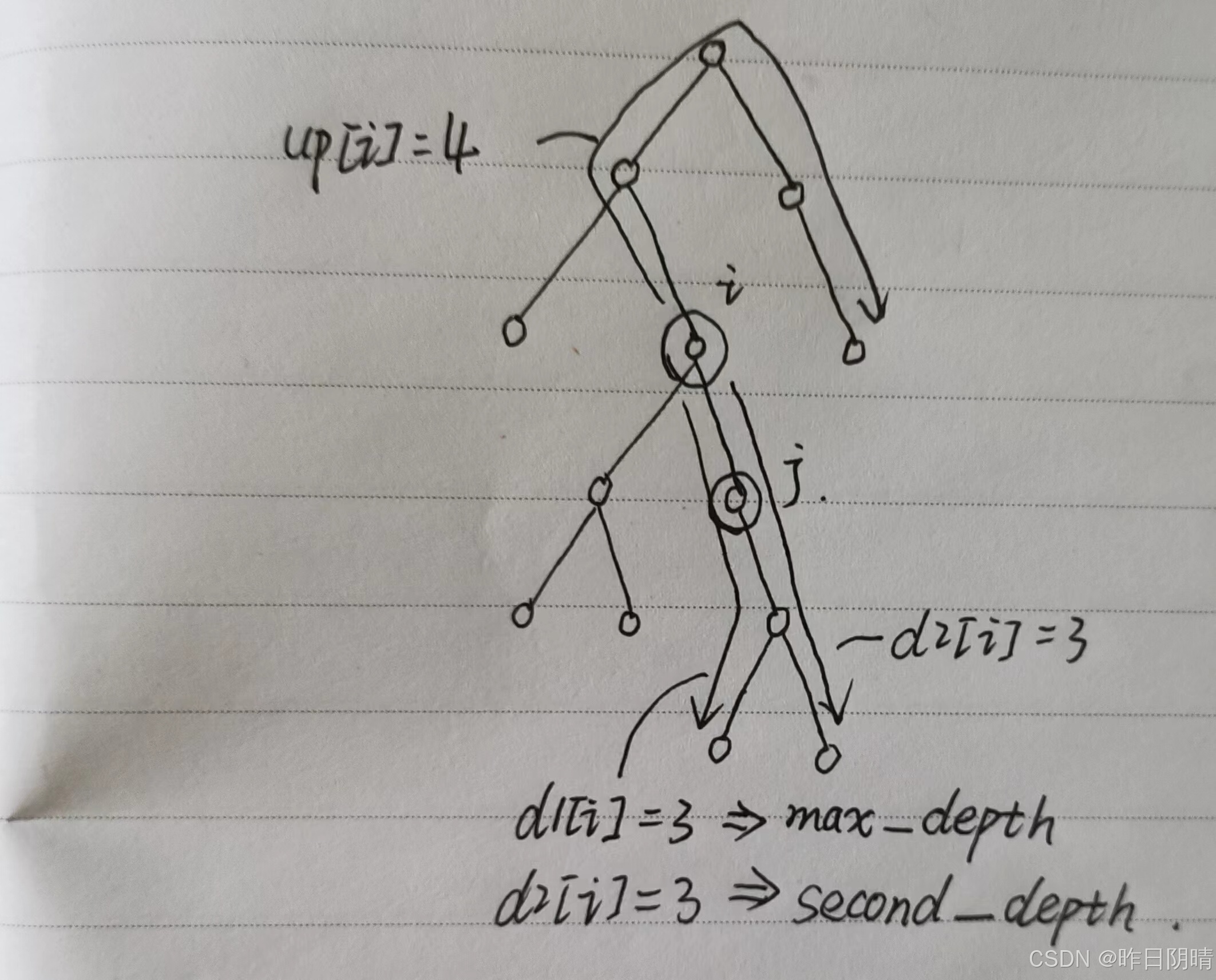
代码 + 注释：

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 10010, M = N * 2, INF = 0x3f3f3f3f;
int n, e[M], ne[M], w[M], h[N], idx;
int d1[N], d2[N], up[N], p1[N]; // 多了一个表示向上的距离数组up[]
bool leaf[N];
void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
int dfs_d(int root, int father) {
    d1[root] = -INF, d2[root] = -INF;
    for (int i = h[root]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == father) continue;
        int d = dfs_d(j, root) + w[i];
        if (d >= d1[root]) {
            d2[root] = d1[root], d1[root] = d;
            p1[root] = j;
        }
        else if (d > d2[root]) d2[root] = d;
    }
    if (d1[root] == -INF) {
        d1[root] = d2[root] = 0;
        leaf[root] = true;
    }
    return d1[root];
}
void dfs_u(int root, int father) {
    for (int i = h[root]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == father) continue;
        if (p1[root] == j) up[j] = max(up[root], d2[root]) + w[i];
        else up[j] = max(up[root], d1[root]) + w[i];
        dfs_u(j, root);
    }
}
int main() {
    scanf("%d", &n);
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i++) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }
    dfs_d(1, -1);
    dfs_u(1, -1);
    int res = d1[1];
    for (int i = 2; i <= n; i++) {
        if (leaf[i]) res = min(res, up[i]);
        else res = min(res, max(d1[i], up[i]));
    }
    printf("%d\n", res);
    return 0;
}

1075.数字转换

题目解析：本题和第一题几乎一样，区别在于本题所表现的东西很隐晦，需要我们自行找出对应的连结节点关系，将约数之和与数的本身建立关系并构造有向图，最终求得该有向图中的直径。

代码 + 注释：

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 50010;
int n;
int sum[N], e[N], ne[N], h[N], idx;
bool st[N];
int res;
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// 求树的直径 -- 模板
int dfs(int u) { // 返回以u为起点的最长距离
    int d1 = 0, d2 = 0;
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        int d = dfs(j) + 1;
        if (d >= d1) d2 = d1, d1 = d;
        else if (d > d2) d2 = d;
    }
    res = max(res, d1 + d2);
    return d1;
}
int main() {
    scanf("%d", &n);
    memset(h, -1, sizeof h);
    for (int i = 1; i <= n; i++) {
        for (int j = 2; j <= n / i; j++) {
            sum[i * j] += i; // 求所有 1~n 之间数字的约数和（不包含其本身）
        }
    }
    for (int i = 2; i <= n; i++) { // 一定要从2开始遍历，否则结果只会为0
        if (sum[i] < i) {
            add(sum[i], i);
            st[i] = true; // 表示 i 有父节点
        }
    }
    for (int i = 1; i <= n; i++) { // 找出根节点进行递归
        if (!st[i]) dfs(i);
    }
    printf("%d\n", res);
    return 0;
}

1074.二叉苹果树

题目解析：

注：f[i][j - x - 1]中的-1是减去i到j的那一段

代码 + 注释：

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 110, M = 2 * N;
int n, last;
int e[M], ne[M], w[M], h[N], idx;
int f[N][N]; // f[i][j] 表示以 i 为根节点保留 j 根树枝所能得到的最大苹果数
void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int u, int fa) {
    for (int i = h[u]; ~i; i = ne[i]) {
        int ver = e[i];
        if (ver == fa) continue; // 无向图需要判断是否与父节点重合
        dfs(ver, u);
        // 有依赖的背包问题 -- 体积划分集合方案
        for (int j = last; j >= 0; j--) {
            for (int k = 0; k < j; k++) {
                f[u][j] = max(f[u][j], f[u][j - k - 1] + f[ver][k] + w[i]);
            }
        }
    }
}
int main() {
    scanf("%d%d", &n, &last);
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i++) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }
    dfs(1, -1);
    printf("%d\n", f[1][last]);
    return 0;
}

323.战略游戏

题目解析：这就是最简单的树型DP问题，在某一结点上放与不放进行状态的构造和转移。

代码 + 注释：

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1510;
int n;
int e[N], ne[N], h[N], idx;
int f[N][2]; // f[i][0/1] 表示在i节点上不放/放士兵
bool st[N];
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int u) {
    f[u][0] = 0, f[u][1] = 1; // 初始化该节点士兵数量
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        dfs(j);
        f[u][0] += f[j][1]; // 若该节点不放士兵，则其子节点必须放
        f[u][1] += min(f[j][0], f[j][1]); // 若该节点放士兵，则其子节点放或不放都可以
    }
}
int main() {
    while (scanf("%d", &n) != -1) {
        memset(h, -1, sizeof h);
        memset(st, false, sizeof st);
        idx = 0;
        for (int i = 0; i < n; i++) {
            int x, num;
            scanf("%d:(%d)", &x, &num);
            for (int j = 0; j < num; j++) {
                int element;
                scanf("%d", &element);
                add(x, element); // 有向图比较省空间
                st[element] = true; // 表示element有父节点
            }
        }
        int root = 0;
        while (st[root]) root++; // 找出没有父节点的节点，就是根节点
        memset(f, -1, sizeof f);
        dfs(root);
        printf("%d\n", min(f[root][0], f[root][1]));
    }
    return 0;
}

1077.皇宫守卫

题目解析：本题和上一题有很大差异，上一题要求我们覆盖掉所有的边，而这一题要求我们覆盖掉所有的节点，因此和上一题不同的是：我们不仅要考虑自身和子节点的放置情况，还要考虑父节点的放置情况，更加复杂一些。

代码 + 注释：

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1510;
int n;
int e[N], ne[N], w[N], h[N], idx;
int f[N][3]; // f[i][0 / 1 / 2] 表示 i 节点 被子节点看守 / 被自己看守 / 被父节点看守
bool st[N];
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int u) {
    f[u][0] = f[u][2] = 0;
    f[u][1] = w[u];
    int sum = 0;
    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        dfs(j);
        // 若 u 被自己看守，则子节点 j 三种情况的看守都有可能
        f[u][1] += min(min(f[j][0], f[j][1]), f[j][2]);
        // 若 u 被父节点看守，则子节点一定不可能被父节点看守
        f[u][2] += min(f[j][0], f[j][1]);
        // 记录下子节点被自己看守或者被子节点看守两种情况取其最小者的和
        sum += min(f[j][0], f[j][1]);
    }
    f[u][0] = 0x3f3f3f3f;
    // 这里计算 u 被子节点看守，就需要筛选出是哪个子节点看守的
    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        f[u][0] = min(f[u][0], sum - min(f[j][0], f[j][1]) + f[j][1]); // 这里是将当时该子节点被看守的情况所需经费减去，再加上如果该子节点放守卫的情况经费
    }
}
int main() {
    scanf("%d", &n);
    memset(h, -1, sizeof h);
    for (int i = 0; i < n; i++) {
        int point, value, num;
        scanf("%d%d%d", &point, &value, &num);
        w[point] = value;
        for (int j = 0; j < num; j++) {
            int son;
            scanf("%d", &son);
            add(point, son);
            st[son] = true;
        }
    }
    int root = 1;
    while (st[root]) root++;
    dfs(root);
    printf("%d\n", min(f[root][0], f[root][1]));
    return 0;
}

昨日阴晴
关注
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值