回顾:上一节我们讲了二叉树的基本知识,今天我们讲一个更加高效的二叉查找树,他支持动态的插入,删除操作
我们之前说过,散列表也是可以支持高效的动态的插入,删除操作,而且时间复杂度是O(1),为何右如此高效的散列表,还需要二叉查找树呢?带着这个问题,我们来学习一下二叉查找树
二叉查找树:顾名思义就是为了快速的查找而诞生的,不仅这样,他还支持高效的动态插入,删除操作,这都依赖于二叉查找树的特殊结构,
结构:在树的任意一个节点,其左子树中的每个节点的值都小于该节点的值,其右子树中的每个节点的值都大于该节点的值,
1>二叉树的查找操作
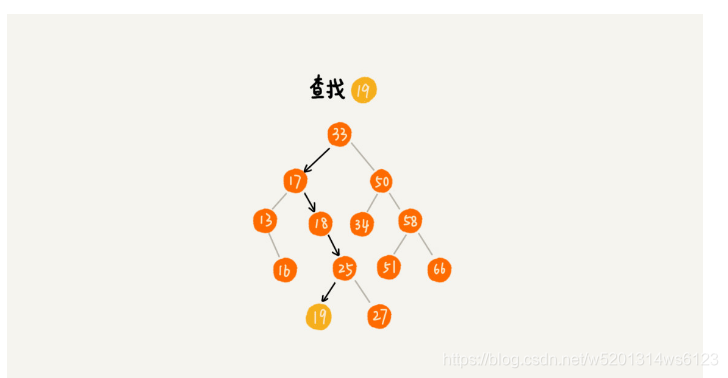
解释:当我们要查找的数字为19,我们以树的根节点为入口,与要查找的19进行相比,如果相等就是我们要查找的元素,如果比根节点大,我们会递归根节点的右子树,直到找到19这个元素,如果比根节点的数字小,我们则去递归根节点的左子树,直到找到我们需要查找的元素.
public class Binarysearchtree{
private Node tree;
public Node find(int data){
Node p = tree;
while(p != null){
if(data < p.data){
p = p.left;
} else if(data > p.data){
p = p.right;
}else{
return p;
}
}
return null;
}
public static class Node{
private int data;
private Node left;
private Node right;
public Node(int data){
this.data = data;
}
}
}
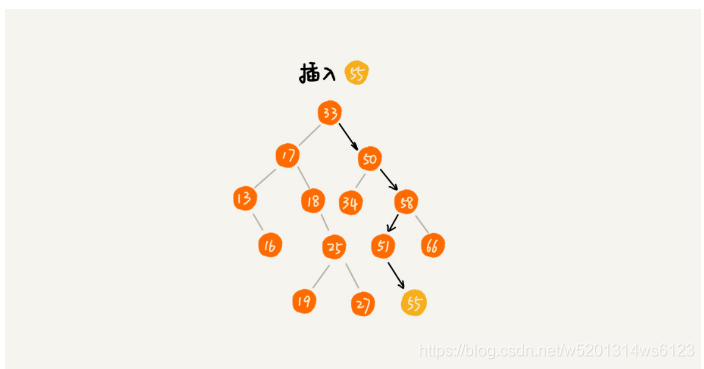
2>二叉查找树的插入操作
二叉查找树的删除操作和二叉查找树的插入操作查不到,我们所要插入的数据都是放在叶子节点的,我们需要从根节点开始,与插入的数据进行比较,如果插入的数据比节点大,且该节点的右子树为空,就进行插入操作,如果不为空,就继续递归遍历该右子树,直到找到插入的位置即可,如果比该节点的数据小,且该节点的左子树为空,就进行插入操作,如果不为空,就继续遍历该节点的左子树,直到找到插入的位置即可.
public class BinaryTree{
private Node tree;
public void insert(int newdata){
if(tree == null){
tree = new Node(data);
return tree;
}
Node p = tree;
while(p != null){
if(p.data < newdata){
if(p.right == null){
p.right = new Node(newdata);
return;
}else{
p = p.right;
}
}else{
if(p.left ==null){
p.left = new Node(newdata);
return;
}
p= p.left;
}
}
public static class Node{
private int data;
private int right;
private int left;
public Node(int data){
this.data = data;
}
}
}
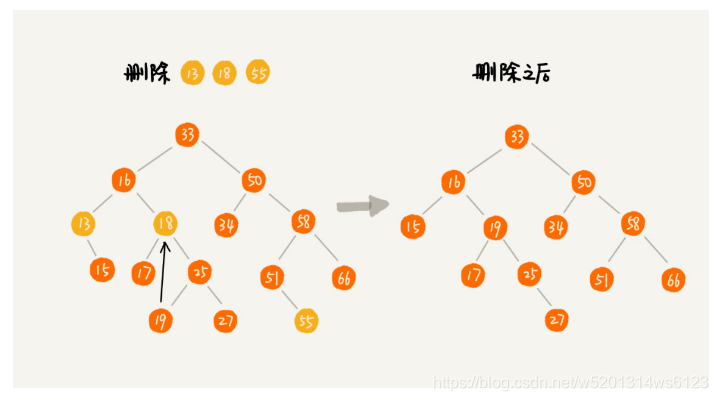
3>二叉查找树的删除操作
1>如果删除的节点没有子节点,我们只需要将父节点中,指向要删除的节点的指针置为null;比如删除55
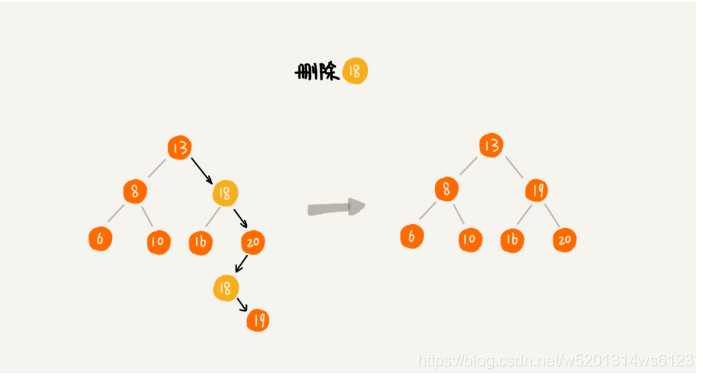
2>如果删除的节点只有一个子节点,我们只需要更新父亲节点中,指向要删除节点的指针,让他指向要删除节点的子节点就可以了,比如图中删除13
3>如果要删除的节点有两个子节点,这就比较复杂了。我们需要找到这.个节点右树中最小节点,把他替换到删除的节点上,然后在删除这个最小节点,因为最小节点肯定没有左节点,比如删除18
4>二叉查找树的其他操作
除了插入删除操作,二叉查找树还支持查找最大节点,最小节点,前驱节点,后继节点,因为二叉查找树的结构就是比较大小的关系进行存储,这是非常方便的.
支持重复数据的二叉查找树(如果在插入元素的过程中,我们遇到与插入数据相同,我们应该怎么处理呢)
1>二叉查找树每个节点不单单可以仅仅可以存放一个数据,如果存在相同的元素,该节点可以是基于链表进行存储的或者可以用支持动态扩容的数组进行存放
2>我们在插入的过程中,如果遇到相同的数据,我们可以把这个数据放在该节点的右子树中,意思就是说,我们把该值意会会大于该节点的值进行存储(实际是相等的)
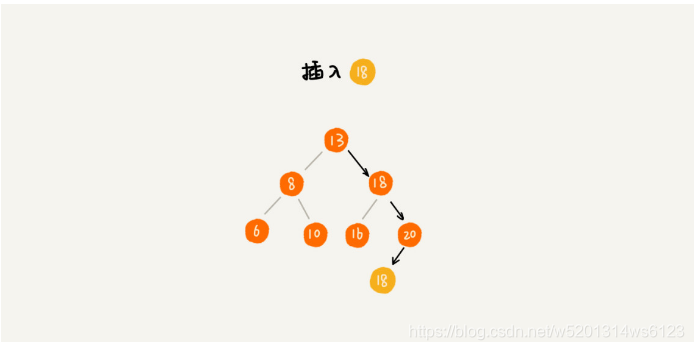
总结:但是我们在查找该元素的时候,我们会花更多的时间去遍历右子树,因为要查找的元素不仅仅只有一个,直到遍历到叶节点就可,这样我们就可以把存在该树中与我们要查找的元素全部取出.
至于删除操作,我们与需要找到每个要删除的节点,然后按照前面的删除操作就可
5>二叉查找树的时间复杂度分析
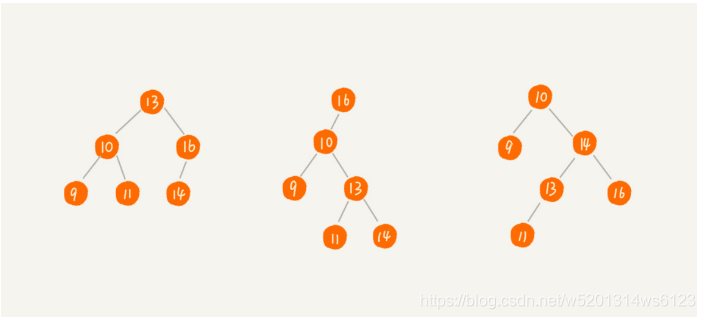
我们先看几种图
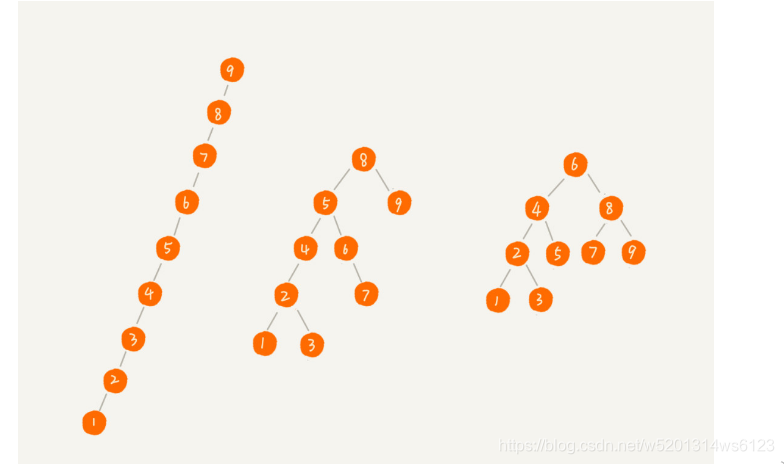
第一副图是最糟糕的二叉树,他已经变成链表结构了,查询的时间复杂度为O(n),显然极度不平衡的二叉查找树已经不满足我们的查询需求,所以我们在建立二叉查找树时候。应该尽量使左右子树达到平衡的状态,这样的时间复杂度为O(logn)
6>解答开篇
1>可以看出,散列表的插入删除的时间复杂度是O(1),而二叉查找树的时间复杂度为O(lohn),很明显散列表的性能更加,但是我们如果要输出一个有序序列,则散列表要先将数据移动到数组进行排序,而二叉查找数据只需要中序遍历即可,
2>散列表在进行频繁的插入数据,需要自动扩容,二自动扩容的本身就比较消耗内存,性能,而且会存在hash冲突,二平二叉查找树性能本身就比较稳定,
3>散列表在设计的时候,要考虑的因素很多,比如设计hash函数,hash冲突解决,装载因子等因素,而二叉树只要考虑平衡问题就可以了.







 本文深入探讨了二叉查找树的结构与操作,包括查找、插入和删除算法,对比散列表性能,分析时间复杂度,并讨论了重复数据处理及平衡问题。
本文深入探讨了二叉查找树的结构与操作,包括查找、插入和删除算法,对比散列表性能,分析时间复杂度,并讨论了重复数据处理及平衡问题。
















 1180
1180

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








