【memcpy和memmove函数的详解】

1.memcpy函数详解

• 模拟实现memcpy函数

2.memmove函数详解

• 模拟实现memmove函数

memset函数详解

memcpy函数

了解一个函数，就查询该函数的相关信息

memcpy函数在库中的声明如下：

void * memcpy ( void * destination, const void * source, size_t num );

memcpy函数是将源头的字符串拷贝num个字节的数据到目标字符串，并返回一个void*的指针，也就是返回目标空间的首地址。

它的含义是：

Copy block of memory

我们知道，strcpy函数是拷贝字符串的，但是它并不能拷贝例如整型，结构体之类的东西，strcpy有一定的局限性，memcpy函数可以说涵盖了所有类型数据的拷贝。

下面直接看一个例子：

int main()
{
	int arr1[] = { 1,2,3,4,5,6,7,8,9,10 };
	int arr2[10] = { 0 };
	memcpy(arr2, arr1+2, sizeof(int)*5);
	//可以拷任意位置的数据，任意字节个数
	for (int i = 0; i < 5; i++)
	{
		printf("%d\n", arr2[i]);
	}
	return 0;
}

在上面的例子中，memcpy是将arr1+2处开始的20个字节拷贝到arr2中，即拷贝3，4，5，6，7
我们可以看一下结果：

既然是一个个字节地拷贝，我们在模拟实现的时候，应该考虑到void的指针应该是转换成char ，才能够满足每个字节地拷贝。

memcpy函数模拟实现

上面说到，memcpy函数是一个个字节地拷贝，拷贝num个字节，我们模拟实现的时候，应该按照库函数的声明来模拟实现。

来看上图，将src中的每一个字节的数据都拷贝到dest中，最后返回dest的首地址，就完成了。

void* my_memcpy(void* dest, const void* src, size_t num)
{
	assert(dest&&src);
	void* ret = dest;
	while (num--)
	{
		*(char*)dest = *(char*)src;
		//dest = (char*)dest + 1;
		//src = (char*)src + 1;
		++(char*)dest;
		++(char*)src;
		/*(char*)dest++;
		(char*)src++;*/  // error，先++，再强转，void*指针无法++
		//((char*)dest)++;
		//((char*)src)++;
	}
	return ret;
}

int main()
{
	int arr1[] = { 1,2,3,4,5,6,7,8,9,10 };
	int arr2[10] = { 0 };
	my_memcpy(arr2, arr1+2, sizeof(int)*5);
	for (int i = 0; i < 5; i++)
	{
		printf("%d\n", arr2[i]);
	}
}

首先应该断言，判断指针的有效性，既然库中的memcpy函数会返回目的地的首地址，所以应该设置一个void*的指针来保存该地址，因为在拷贝的过程中，目的地的地址会不断变化，在上面模拟实现的过程中，注释的几个代码都是可以实现的。

结果如上图所示：

不知道你是否想过一个问题，对于memcpy函数而言，假如我想要拷贝自己，假如把自己的3，4，5，6，7拷贝到1，2，3，4，5中，能不能实现呢？

就我现在模拟实现的函数而言，是无法实现的，因为在拷贝的过程中，自身的值会发生改变，也就变成了1 2 1 2 1 2 1 8 9 10

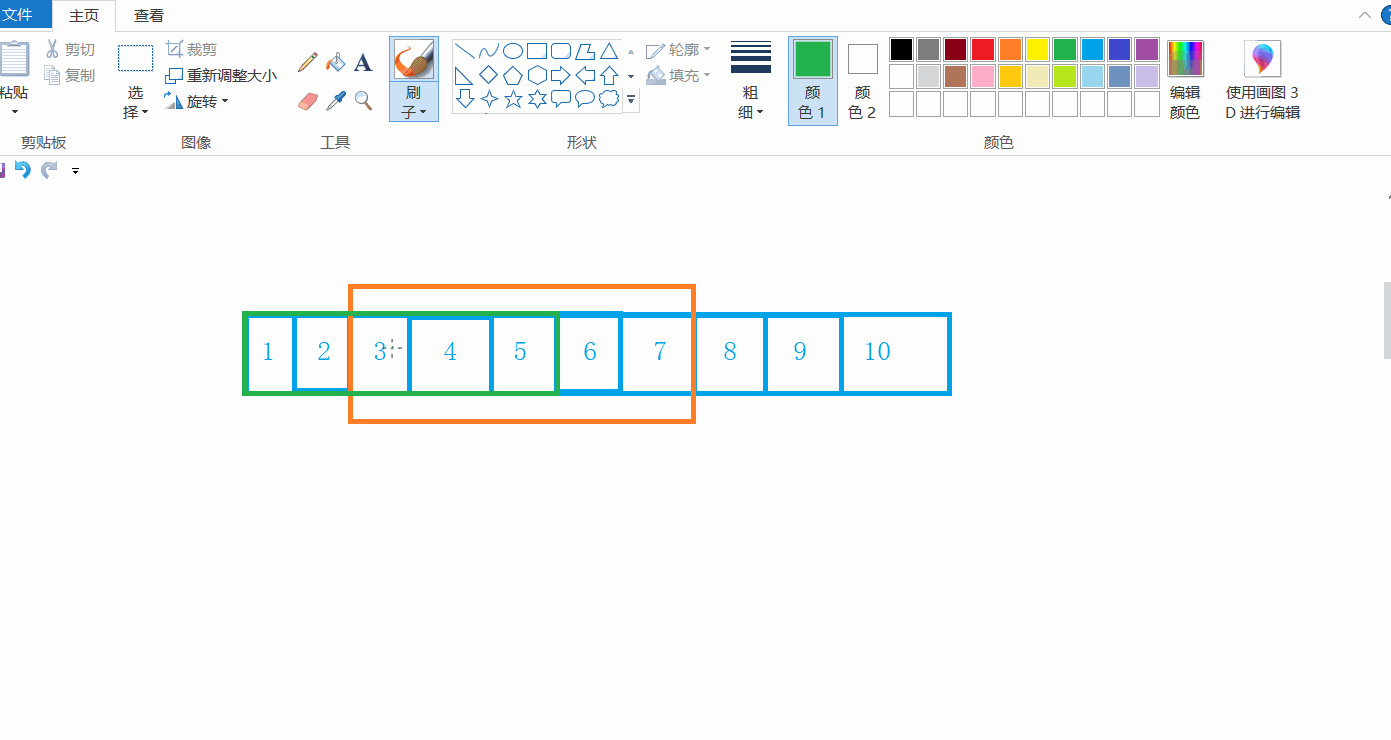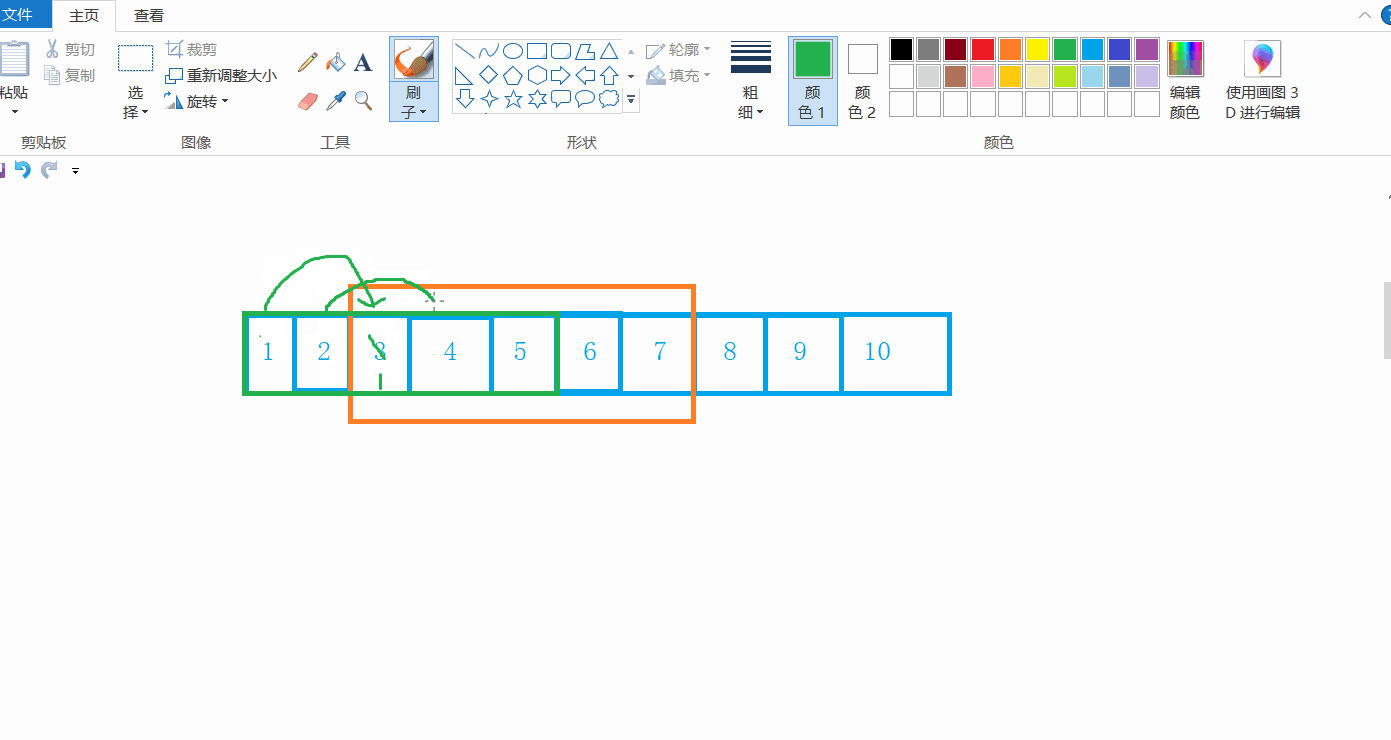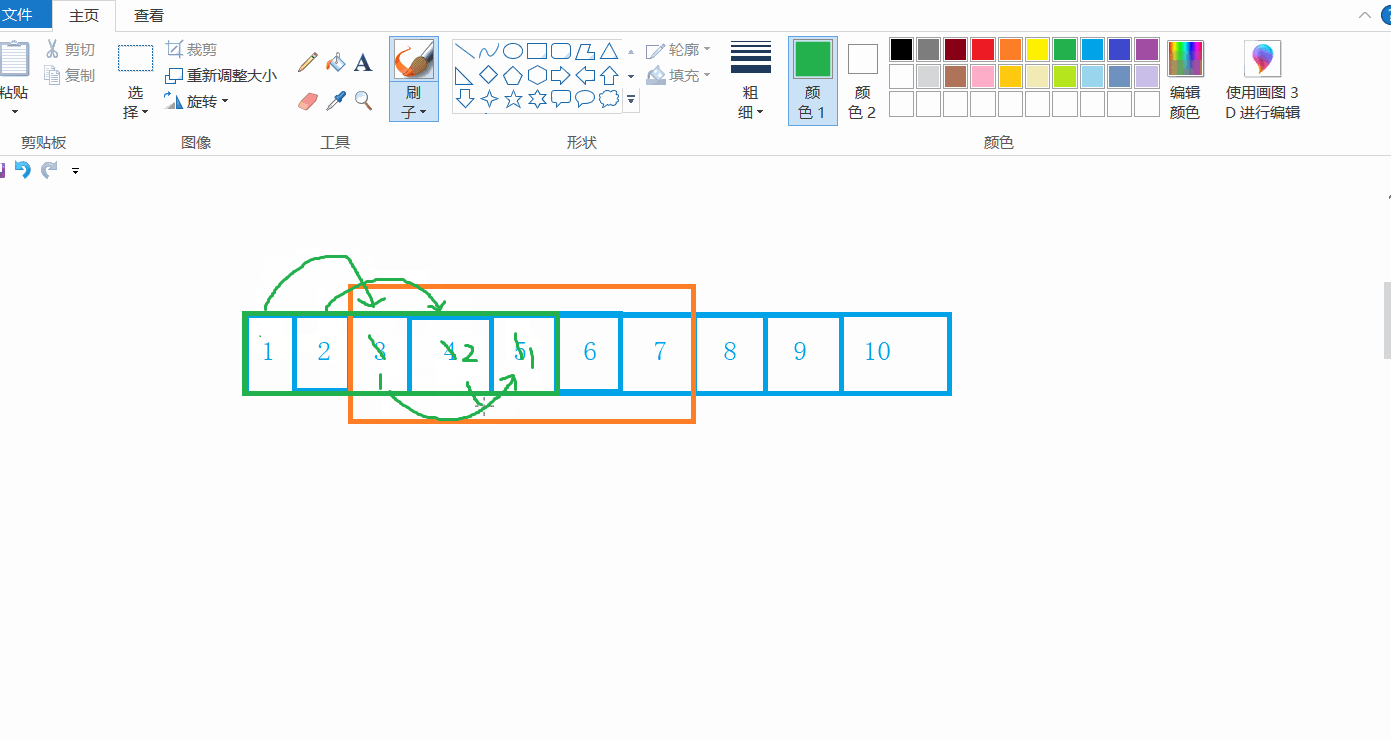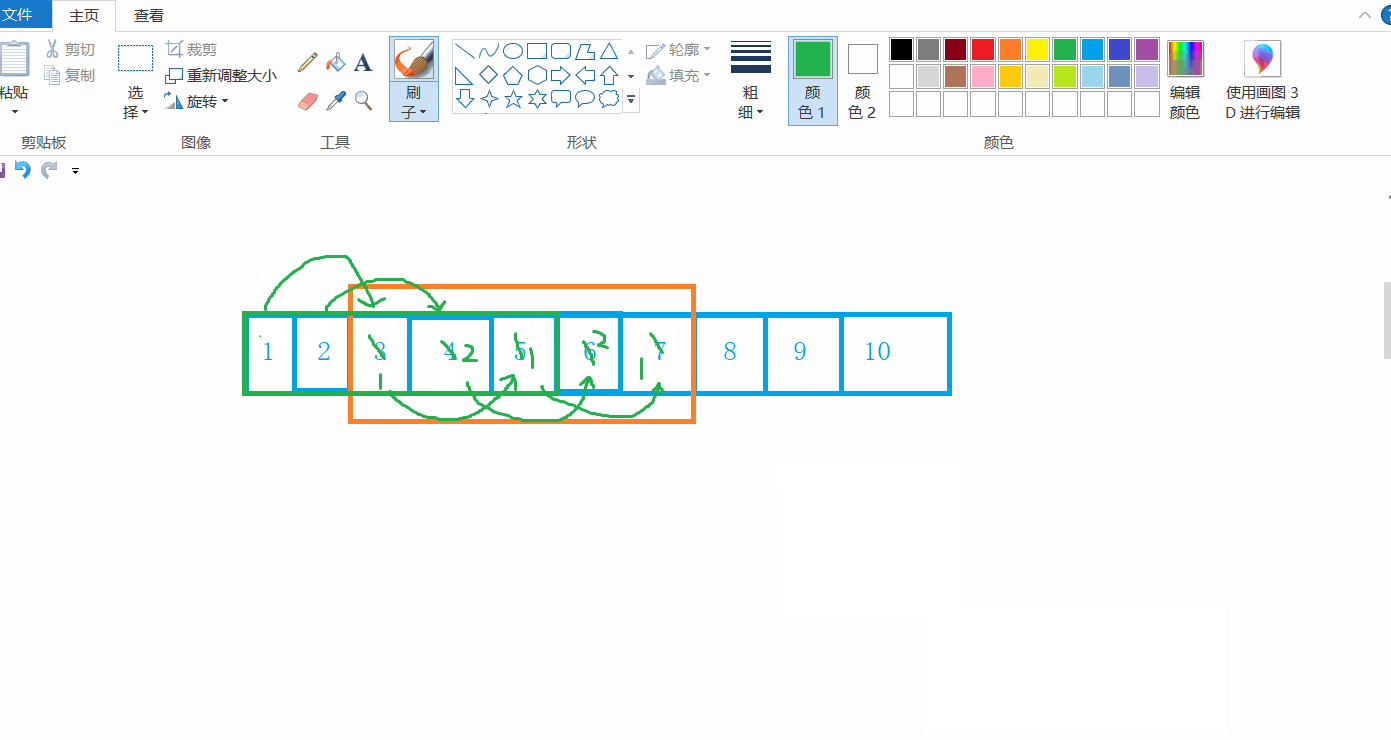
那么，针对这一问题，就有一个函数能够解决：memmove函数

(实际上，库里面的memcpy函数能够完全实现memmove函数的功能，可以说memcpy超额完成任务)

memmove函数

memmove函数其实是更有针对性地对于有重叠数据的拷贝而诞生的。

就像上面的例子，假如拷贝的数据有重叠，就需要用到memove函数。

void * memmove ( void * destination, const void * source, size_t num );

函数声明与memcpy函数相同。

还是上面的例子，使用memmove能够完美实现拷贝重叠部分。

int main()
{
	int arr1[20] = { 1,2,3,4,5,6,7,8,9,10 };
	int arr2[10] = { 0 };
	mmemmove(arr1+2, arr1, sizeof(int) * 5);
	for (int i = 0; i < 10; i++)
	{
		printf("%d\n", arr1[i]);
	}

结果如下：

那么，memmove函数的工作原理到底是什么呢？

在上面的例子中，不管目标位置是否大于原位置，memcpy拷贝的时候都是从前往后拷贝，这才导致拷贝不成功，但是当我们从后往前拷贝呢？

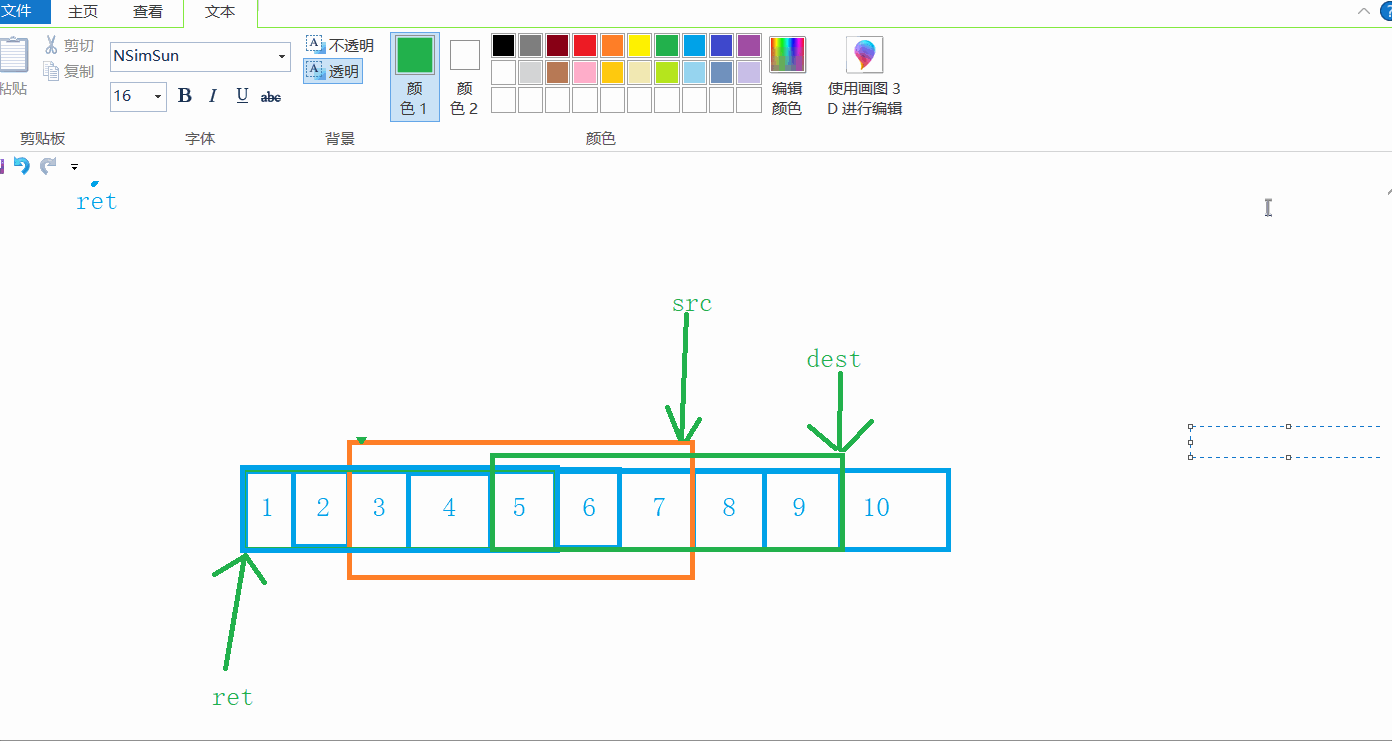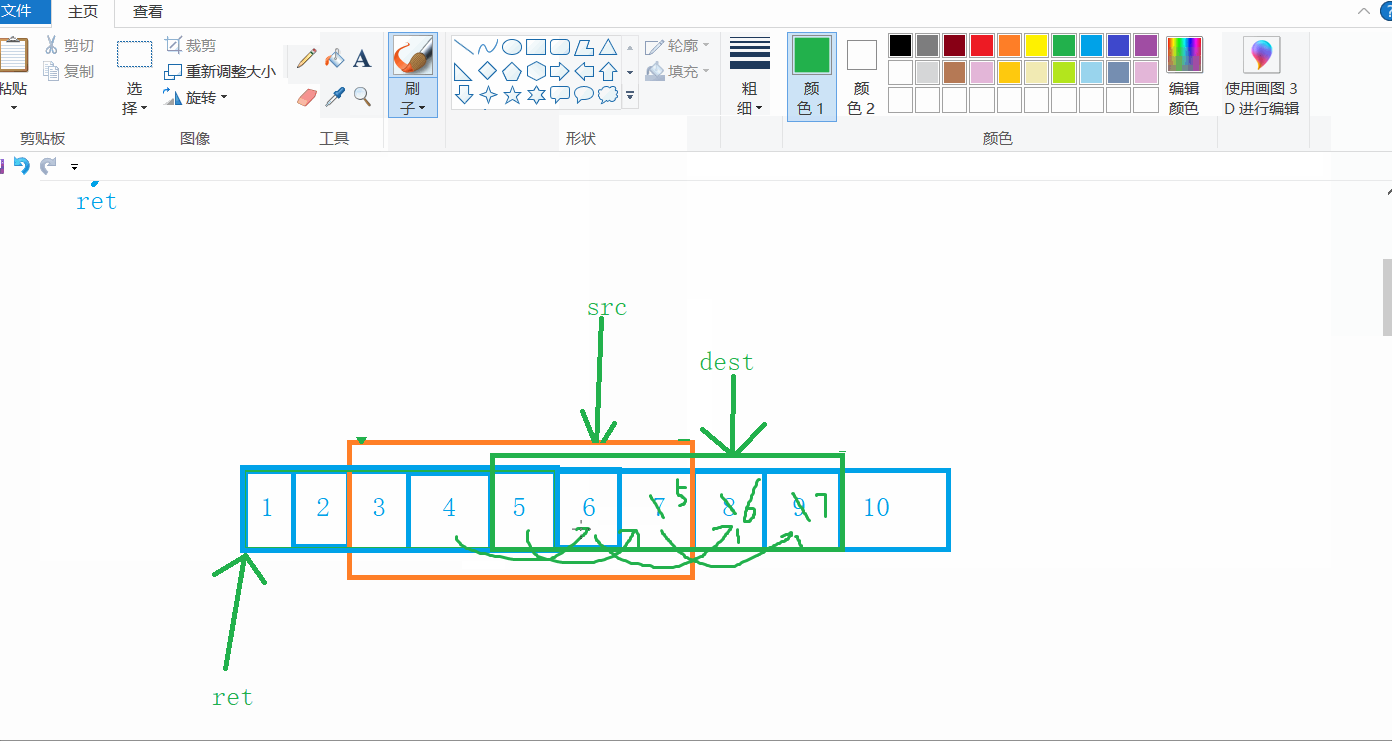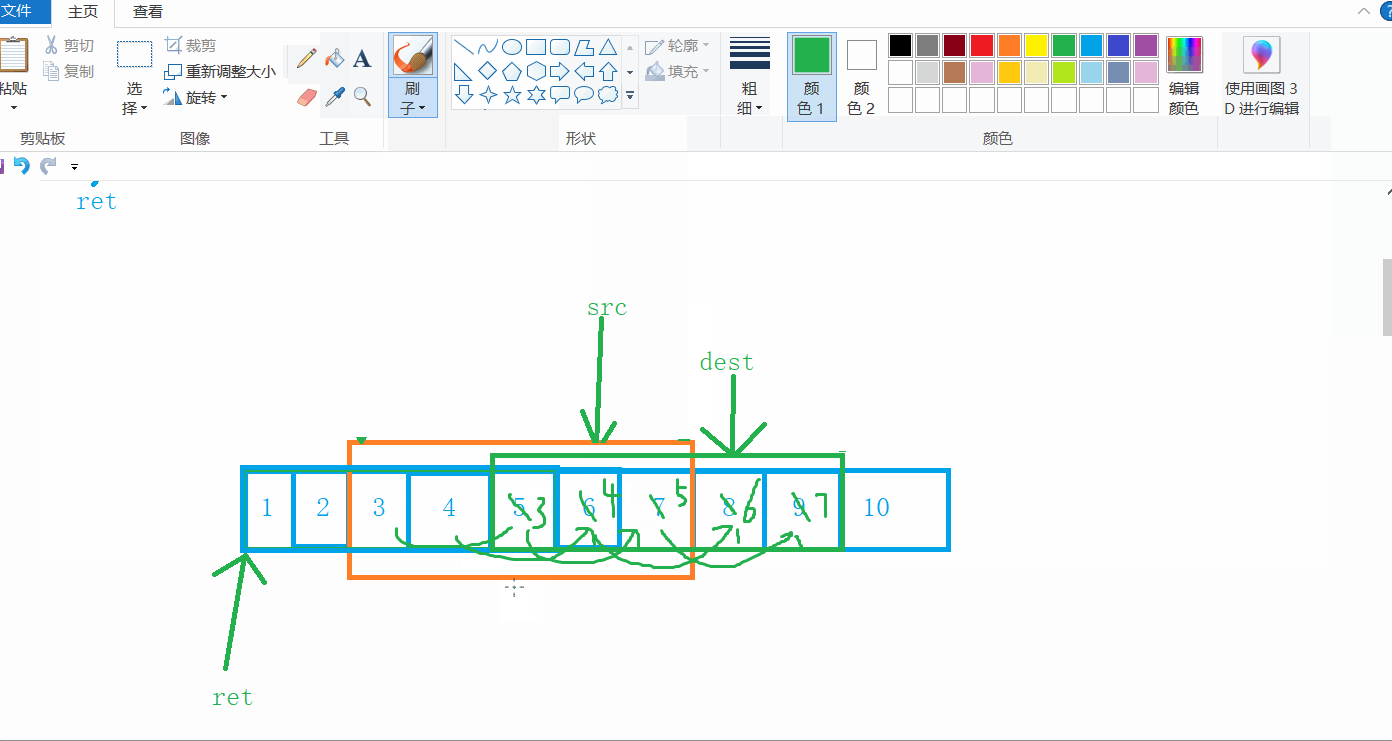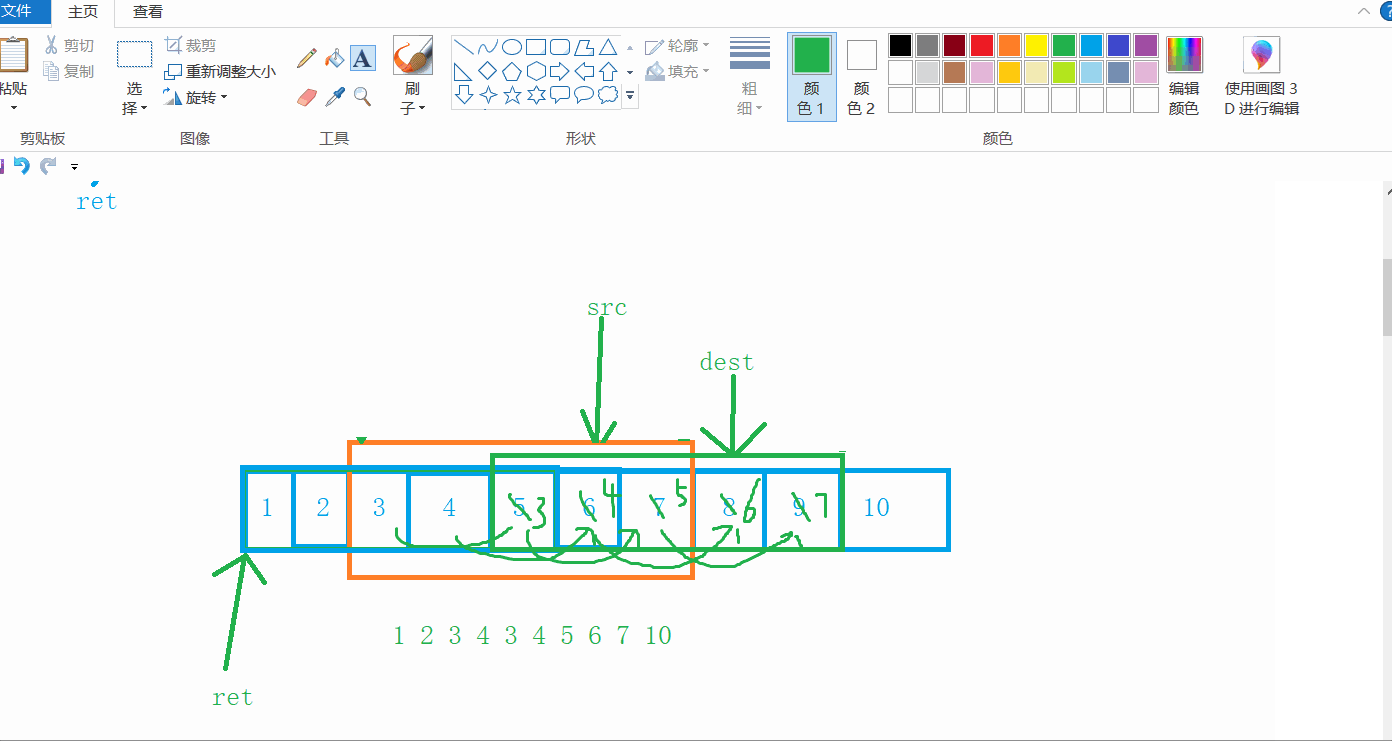
可以看到，当dest的位置大于src位置时，从后往前拷贝是没有问题的，那么假如dest的位置小于src的位置呢？
是否还是一直从后往前拷贝？
一直从后往前拷贝过于绝对。

当dest的位置小于src的位置时，从前往后拷贝是合适的。

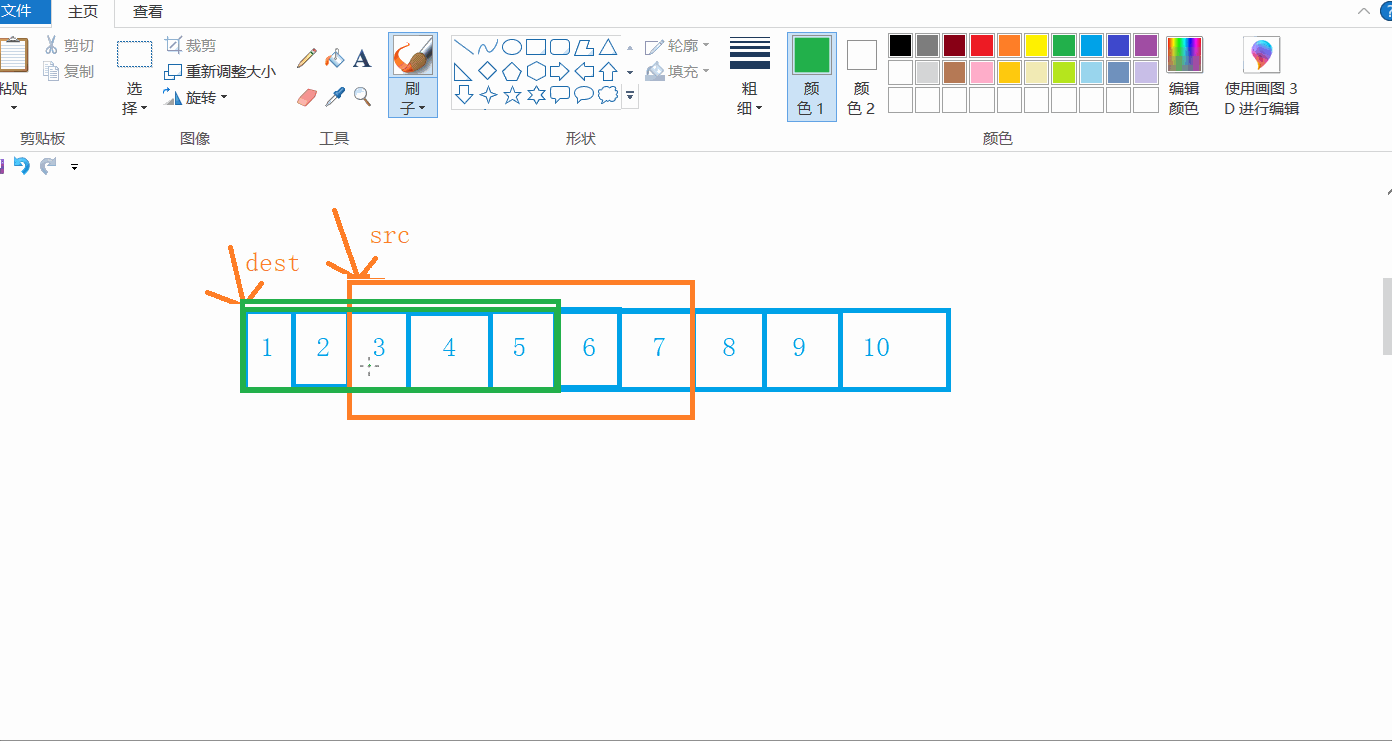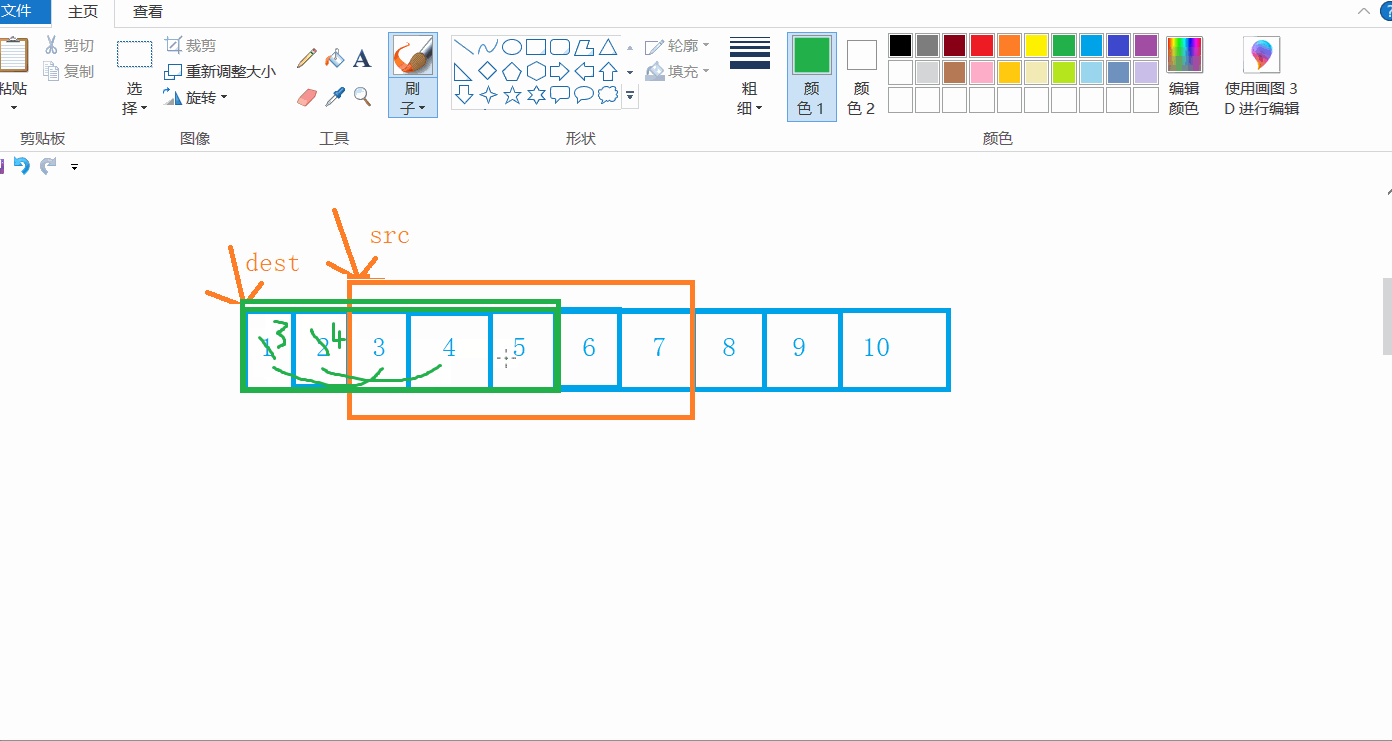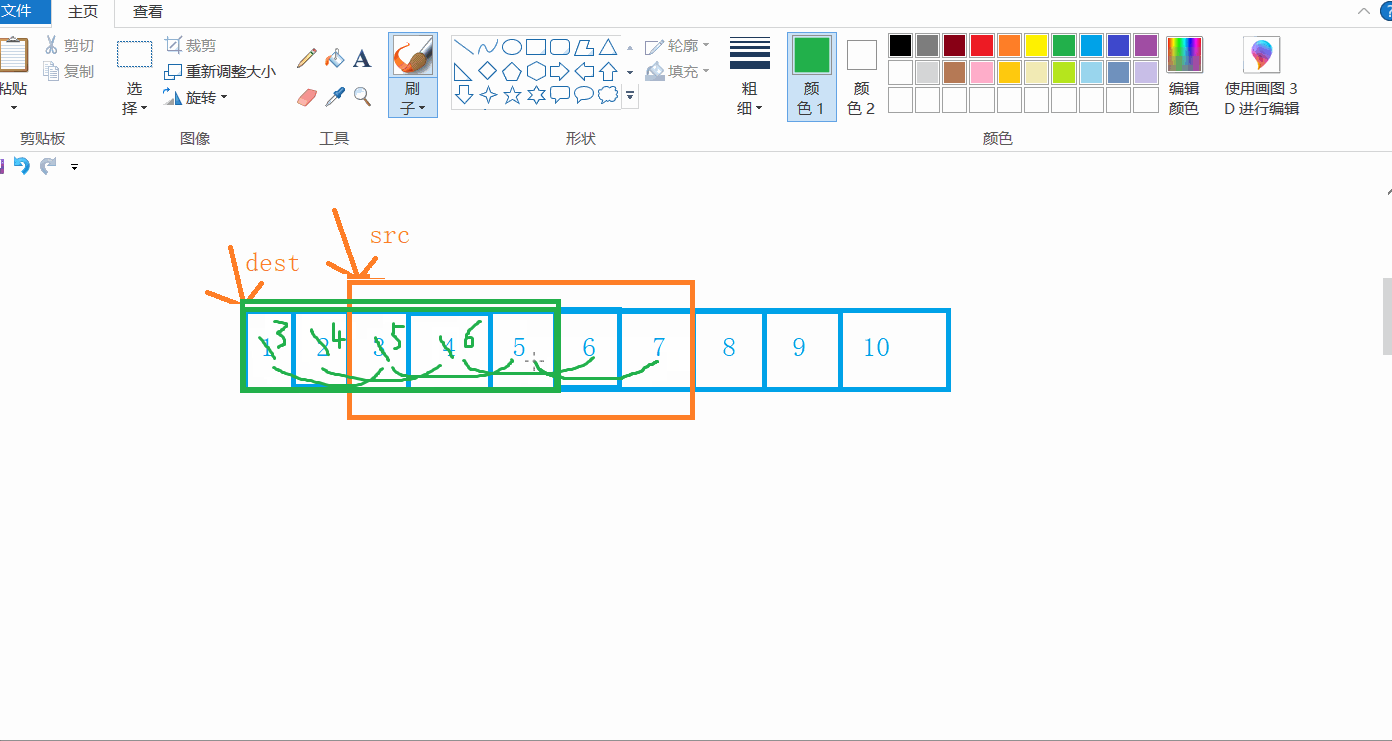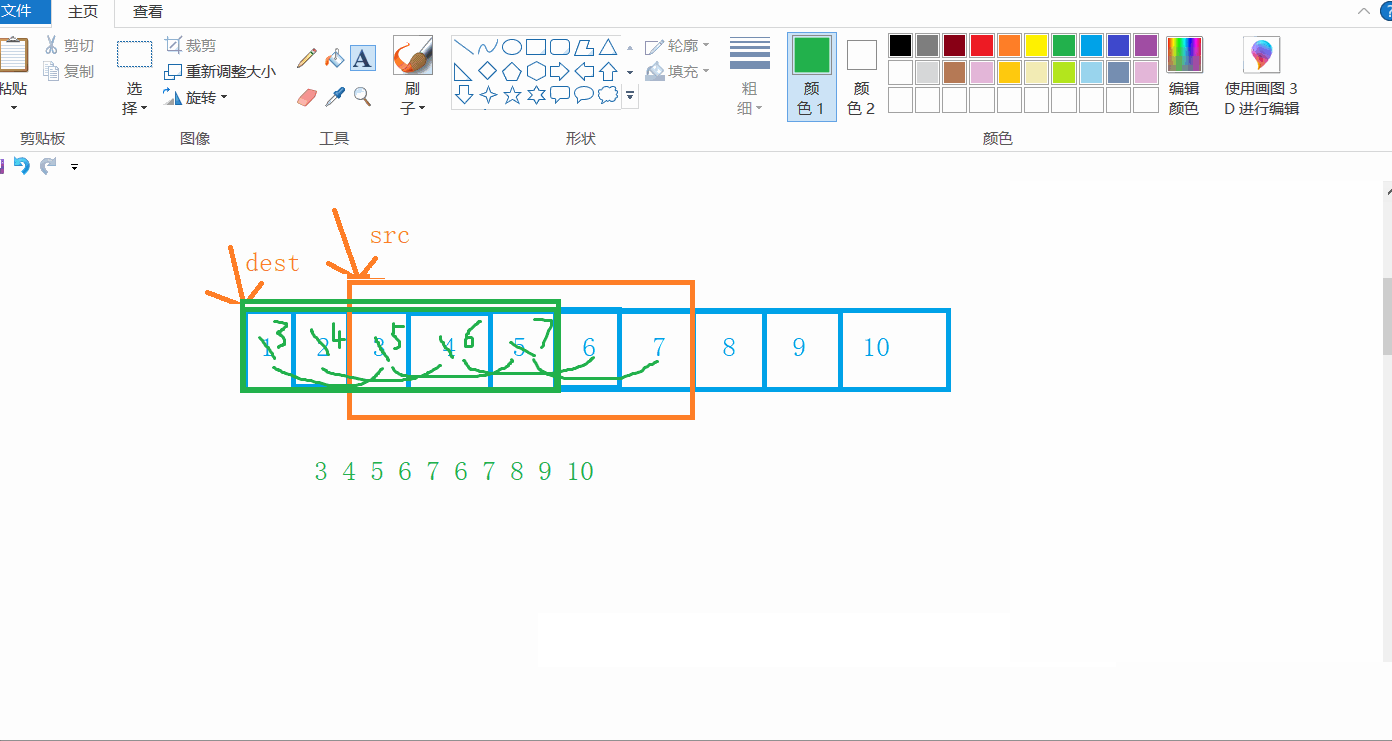
当dest>src，并且超出了src的范围呢？

就像这样，其实，这种情况已经是不重叠的情况了，也就是使用memcpy的方式处理，我们在拷贝的时候，必须保证目标空间足够大，所以不可能存在越界拷贝的情况。

所以在这第三种情况的时候，无论从前往后拷贝，还是从后往前拷贝，都是可以的。
我们不如从后往前拷贝，这样就使问题简单多了。

所以我们得出结论：

当dest<src -->从前往后拷贝
当dest>src，从后往前拷贝

图解如下：

下面就可以开始模拟实现了：

memmove函数模拟实现

有了上面的理解，模拟实现就好办了。

void* my_memmove(void* dest, const void* src,size_t num)
{
	assert(dest && src);
	void* ret = dest;
	if (dest < src)
	{
		// 前->后
		while (num--)
		{
			*(char*)dest = *(char*)src;
			((char*)dest)++;
			((char*)src)++;
		}
	}
	else // 后->前拷贝 
	{
		while (num--)
		{
			*((char*)dest + num) = *((char*)src + num); //首先要找到最后一个字节
				//不用count -1,进入循环时，count已经--了
		}
	}
	return ret;
}

memset函数

void * memset ( void * ptr, int value, size_t num );

该函数的含义是：

该函数是一个设置函数，将指定的内存设置成指定的值。

什么意思呢？
举个例子：

int main()
{
	char arr[] = "hello world";
	memset(arr, 'x', 5);
	memset(arr+6, 'y', 5);
	printf("%s\n", arr);
	return 0;
}

该函数的意思是：将arr中的前 5 个字节设置成x，将arr的第6个字节开始的后五个字节设置成y。
注意：单位是字节，也就是一个一个字节地设置。

看下面的例子：

int main()
{
	int arr[10] = { 0 };
	memset(arr, 1, 40);
	return 0;
}

这样设置，会不会让arr中的10个元素都设置成1呢？

不会。

注意：单位是字节，是一个个字节地设置。

将16进制转换成十进制，与上图结果相符。