标题：使用Python实现简单计算器功能

首先：

1.掌握Python的基础语法数据类型

2.熟悉控制结构和函数的正确调用

3.注意变量的定义

接着进行函数定义：

1.我们首先定义一个名为Caculator的函数。这个函数将负责根据用户输入的操作符和数字进行相应的计算。

2.在函数内部，我们使用input函数获取用户想要进行的操作（1表示加法，2表示减法，3表示乘法，4表示除法，5表示幂运算）以及两个操作数a和b

操作判断：

1.使用if-elif-else语句来判断用户选择的操作。

2.对于加法操作（choose=="1"），计算a+b并打印结果。

3.对于减法操作（choose=="2"），计算a-b并打印结果。

4.对于乘法操作（choose=="3"），计算a*b并打印结果。

5.对于除法操作（choose=="4"），计算a/b并打印结果。

6.对于幂运算操作（choose=="5"），计算a**b并打印结果。

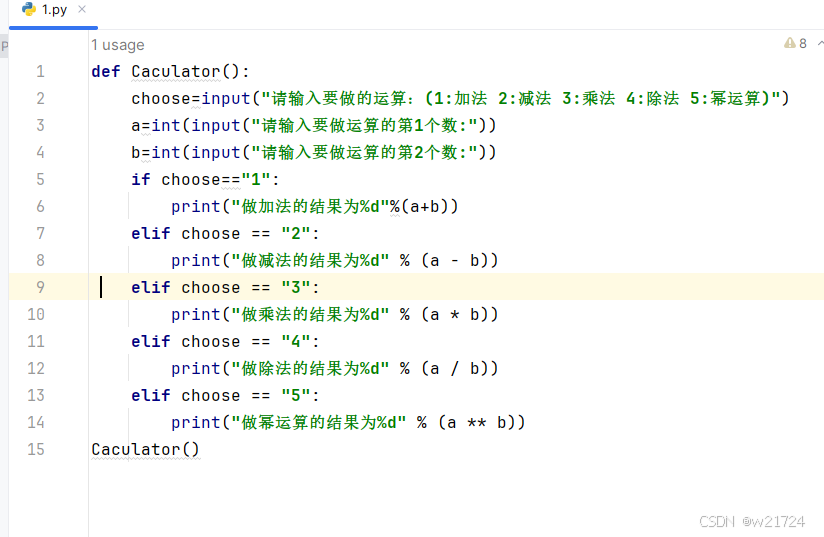
代码示例：

def Caculator():
    choose=input("请输入要做的运算：(1:加法 2:减法 3:乘法 4:除法 5:幂运算)")
    a=int(input("请输入要做运算的第1个数:"))
    b=int(input("请输入要做运算的第2个数:"))
    if choose=="1":
        print("做加法的结果为%d"%(a+b))
    elif choose == "2":
        print("做减法的结果为%d" % (a - b))
    elif choose == "3":
        print("做乘法的结果为%d" % (a * b))
    elif choose == "4":
        print("做除法的结果为%d" % (a / b))
    elif choose == "5":
        print("做幂运算的结果为%d" % (a ** b))
Caculator()

运行结果：

1.加法示例：

当用户输入操作1，第一个数5，第二个数3时，运行结果为：

           请输入要做的运算：(1:加法 2:减法 3:乘法 4:除法 5:幂运算)1

           请输入要做运算的第1个数:5

           请输入要做运算的第2个数:3

            做加法的结果为8

2.减法示例：

当用户输入操作2，第一个数5，第二个数3时，运行结果为：

           请输入要做的运算：(1:加法 2:减法 3:乘法 4:除法 5:幂运算)2

           请输入要做运算的第1个数:5

           请输入要做运算的第2个数:3

            做减法的结果为2

3.乘法示例：

当用户输入操作3，第一个数5，第二个数3时，运行结果为：

           请输入要做的运算：(1:加法 2:减法 3:乘法 4:除法 5:幂运算)3

           请输入要做运算的第1个数:5

           请输入要做运算的第2个数:3

            做加法的结果为15

4.除法示例：

当用户输入操作4，第一个数6，第二个数2时，运行结果为：

           请输入要做的运算：(1:加法 2:减法 3:乘法 4:除法 5:幂运算)4

           请输入要做运算的第1个数:6

           请输入要做运算的第2个数:3

            做除法的结果为3

5.幂运算示例：

当用户输入操作5，第一个数5，第二个数3时，运行结果为：

           请输入要做的运算：(1:加法 2:减法 3:乘法 4:除法 5:幂运算)5

           请输入要做运算的第1个数:5

           请输入要做运算的第2个数:3

            做幂运算的结果为125

图片示例：

进行相关操作选择运行出结果

最后总结：通过这个简单的Python计算器程序，我们可以看到如何使用函数和条件判断来实现基本的数学运算功能。这种方法可以很容易地扩展到更复杂的计算需求。

问：如何用Python语言计算点与点之间的距离？

1.导入math模块,因为在计算欧几里得距离时，需要使用到平方根函数sqrt。

2.定义欧几里得距离函数 

def  euclidean_distance(point1,point2):

x1,y1=point1

x2,y2=point2

return math.sqrt((x2-x1)**2+(y2-y1)**2)

3.定义寻找最大距离的函数

4.运行函数并输出结果。