基于基线最小二乘法的路径拟合

曲线拟合基于基线最小二乘法的树莓派小车路径

摘要

曲线拟合在工程设计、计算机图形学等领域有广泛应用。在某些情况下，传统最小二乘法无法充分使用已知条件，因此我们引入了一个称为基线的概念。我们首先估计一条基线，并将点到直线距离作为概率密度的参数，用作最小二乘法的权重值。我们开发的软件表明，该方法所需的运行时间更短，且能获得更好的拟合结果。

1. 引言

在某些情况下，我们想要用一些散点拟合若干条直线。采用了总体最小二乘法（TLS）、加权总体最小二乘法（WTLS）[1,2,3]、稳健加权总体最小二乘法（RWTLS）这些方法来进行直线拟合。然而，在某些特殊情况下，我们有更好的选择来拟合这些直线。如果我们有一条基线，就可以使用一些简单的权重值，按照不同的权重对点集进行划分。基线的选择取决于具体情况。在大多数情况下，我们可能不会将基线作为最终结果。

有一些类似的方法，如分段最小二乘法、多重自适应最小二乘法和移动最小二乘法。[4,5,6]但由于引入了基线的概念，我们的软件需要更少的运行时间，并且能够获得更好的拟合结果。点到直线距离是算子的参数，我们选择不同的概率密度作为权重值。

本文结构如下。在第2节中，我们将测试线性最小二乘法中使用各种权重以获得最佳拟合直线。在第3节中，我们讨论实验结果。探索汽车行驶路线的主要因素 该研究的应用范围看似狭窄，将在第4节中进行讨论。

2. 方法

最小二乘法要求残差平方和最小，这比绝对值之和更优。观测表明，这些点分布在一条直线两侧附近。因此可以确定数学模型：

$$
y = ax + b
$$

根据最小二乘法，我们需要进行

$$
\sum_{i=1}^{n}(y_i - (ax_i + b))^2
$$

得到它的最小值。这意味着我们应该使

$$
\frac{\partial}{\partial a}\sum_{i=1}^{n}(y_i - (ax_i + b))^2 = 0,\quad \frac{\partial}{\partial b}\sum_{i=1}^{n}(y_i - (ax_i + b))^2 = 0
$$

有三种常见的概率分布适用于线性最小二乘法的条件。自变量X选择为测量点到基准线的距离。基准线来自建筑物内部的实际地图。

第一种是均匀分布。在这种情况下，权重可以表示为：

$$
w_i = 1
$$

在这种情况下，权重可以省略。

第二种是指数分布。这种情况下的权重可以写成：

$$
w_i = e^{-\lambda d_i}
$$

第三种是正态分布。它的权重如下：

$$
w_i = e^{-\frac{d_i^2}{2\sigma^2}}
$$

将(4)代入(2)，得到以下方程：

$$
\sum_{i=1}^{n} w_i (y_i - (ax_i + b)) x_i = 0,\quad \sum_{i=1}^{n} w_i (y_i - (ax_i + b)) = 0
$$

在上述方程中，$a_1$ 和 $b_1$ 表示基线的参数。$a$ 和 $b$ 表示数学模型的参数。

将(5)代入(2)，得到以下方程：

$$
\sum_{i=1}^{n} w_i (y_i - (ax_i + b)) x_i = 0,\quad \sum_{i=1}^{n} w_i (y_i - (ax_i + b)) = 0
$$

这里我们使用标准正态分布，即 $\sigma= 1$, $\mu= 0$。

然后我们使用二范数计算公式的精度。

2.1 数据集详细信息

我们演示如何利用预先测量的数据集来使用该公式。控制一辆树莓派小车在平坦道路上直线行驶十秒。每经过十秒，在结束时通过Wi-Fi获取位置坐标。[7]将位置转换为二维坐标系中的一个点。

基线由实际地图转换而来。由于在现实世界中无法避免测量误差，并且距离基线越近的点具有更高的概率权重，因此我们采用基线最小二乘法来获得小车的实际路线。在本实验中，使用最后30%的数据集来测试该方法的精度。

2.2 工作流程

整体工作流程如图1所示。首先，系统需要一些前置Python包，包括numpy版本1.12.1、pandas版本0.19.2、Pillow版本4.1.0。这些Python包在许多系统中已预安装，但如果未安装，用户可使用“pip”手动安装，例如： pip install numpy 。

3. 结果

测量汽车在x坐标处的y坐标，如下表1。

表1. 汽车行驶坐标

测量点	x / m	y / m
1	4.1	10.8
2	10.0	15.25
3	15.1	21.8
4	21.0	25.35
5	25.0	30.9
6	30.1	35.1
7	35.0	40.7
8	40.1	45.25
9	45.0	50.3
10	50.0	55.6
11	55.1	60.45
12	60.1	65.05
13	65.0	70.2
14	70.2	75.3
15	75.1	80.5
16	80.0	85.4
17	85.1	90.3
18	90.0	95.25
19	95.0	100.8
20	100.0	105.45

基线的表达式为 $ y = x $，也就是说，$ a_1 = b_1 = 1 $。将测量值代入公式6，得到指数分布的图像。将测量值代入公式7，得到正态分布的图像。

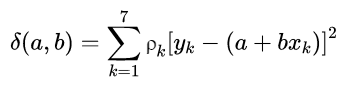
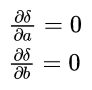
经过五组测试后，我们得到了公式的精度平均值。

方法	精度 (m)	运行时间 (s)
LS	0.56	1.0
PLS	0.21	3.2
我们的方法_指数	0.22	1.3
我们的方法_普通	0.19	1.4

该系统的代码可在 https://github.com/vsfh/WeighedLeastQuare 获取

4. 结论

采用一种易于使用的方法来获取多个点的合适直线。该方法的精度优于其他最小二乘算法。它不仅可以用于地图绘制，还可应用于某些特殊情况。通过测量基线与估计线之间的误差，可以推导出车辆轮胎的磨损情况。该方法也可应用于风洞实验。当然，这些应用需要更多的实验研究和假设验证。