Transformer架构
- encoder: input ---> input_embeddings + positional encoding---> (mha ---> add&norm --->feed forward ---> add&norm) * n ---> o1
- decoder: output ---> output_embeddings + positional encoding ---> (mmha ---> add&norm ---> + o1 ---> mha ---> add&norm ---> feed forward ---> add&norm) * n ---> linear ---> softmax ---> output probabilities
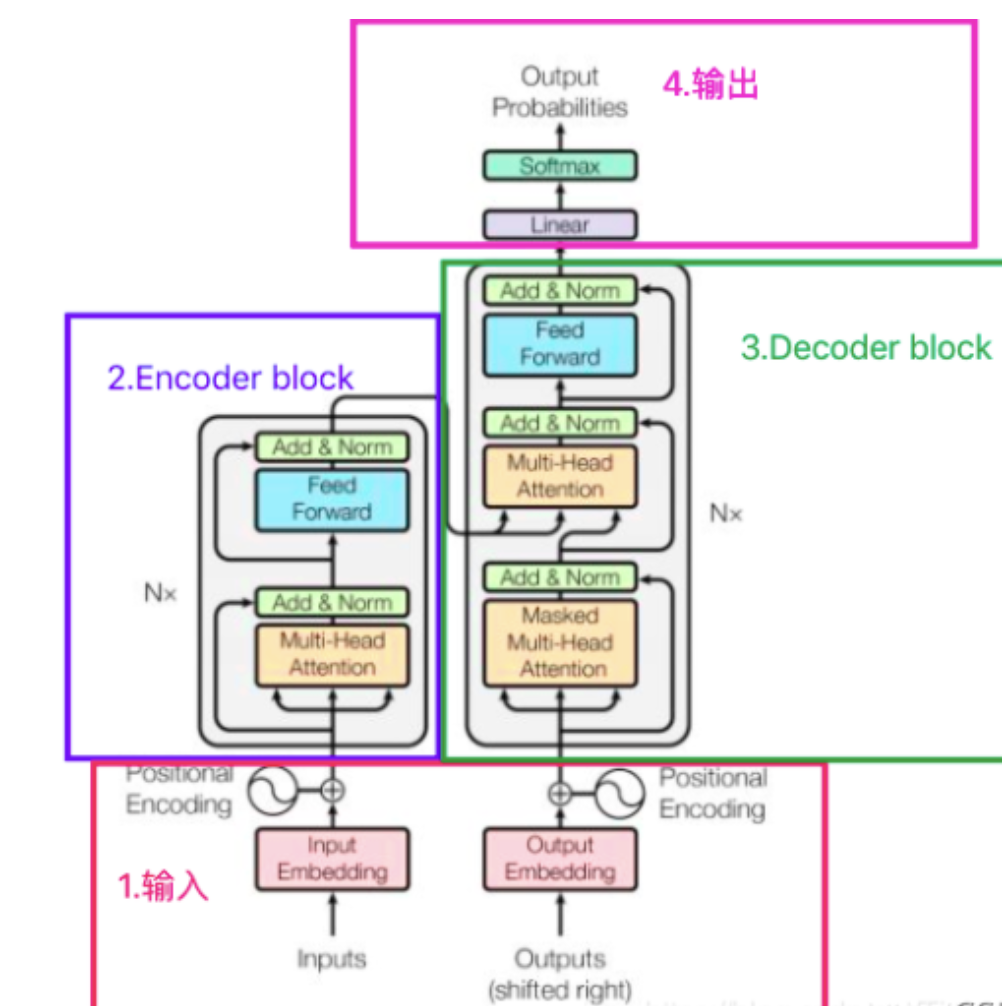
后面主要是decoder结构的介绍。(decoder与encoder相比,有两个mha, 第一个用了sequence mask, 第二个的k 和 v 是由encoder的输出来计算, q是上一个decoder的输出)
对比图如下所示:
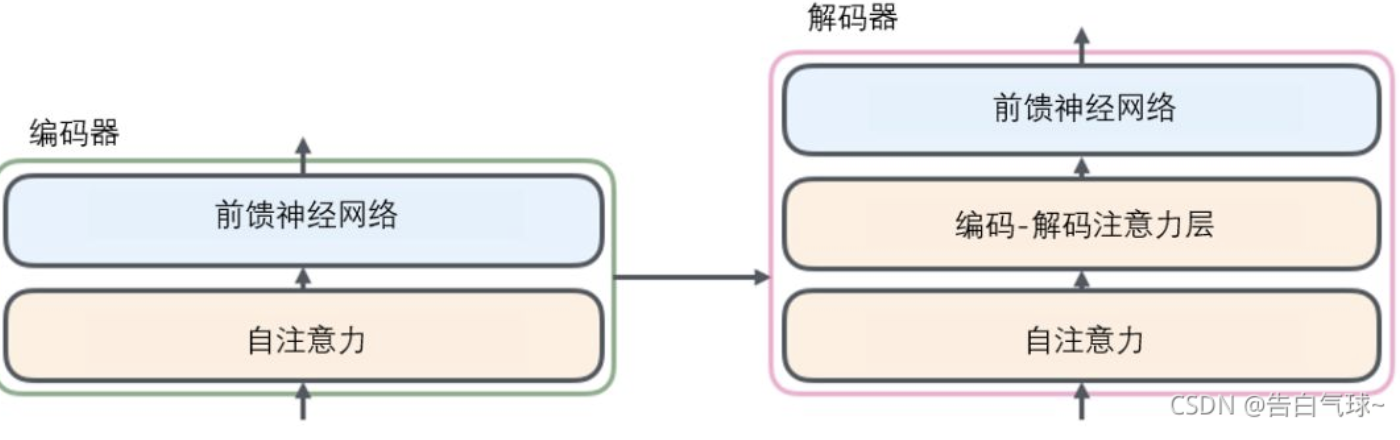
Positional encoding
- 作用:提取输入的顺序关系,来区分不同位置的token之间的差异。
- 实现方法:将位置信息融合到输入中(绝对位置编码) | 微调Attention结构,使之有能力分辨不同位置的token(相对位置编码)
1. 绝对位置编码
在输入的第k个向量中加入位置向量,即
。
1.1. 训练式
直接将位置编码当作可训练参数。
1.2. 三角式
对于位置k的编码向量,
偶数位置分量的编码向量 表示为
奇数位置分量的编码向量 表示为
其中,
1.3. 递归式
从一个向量p0出发,通过递归格式p_{k+1}=f(pk)来得到各个位置的编码向量
2. 相对位置编码
在算Attention的时候考虑当前位置与被Attention的位置的相对距离
2.1. 经典式
绝对位置编码关注的是 “我是第几个词”, 但是 相对位置编码关注的是 “我相对于你的位置是什么”
假设我们计算第i个词对第j个词的注意力,它们之间的相对距离是 i - j(或 j - i,取决于定义)。
新增的部分,计算的是位置偏置。
是一个可学习的向量,表示两个位置相距的相对关系。
2.2. XLNET式
直接将替换为相对位置向量
,至于两个
,则干脆替换为两个可训练的向量u,v
3. MHA
3.1. self-attention
自注意力会关注整个输入序列的所有单词,帮助模型对本单词更好地进行编码.
对于输入向量,乘以权重矩阵得到查询向量、键向量和一个值向量
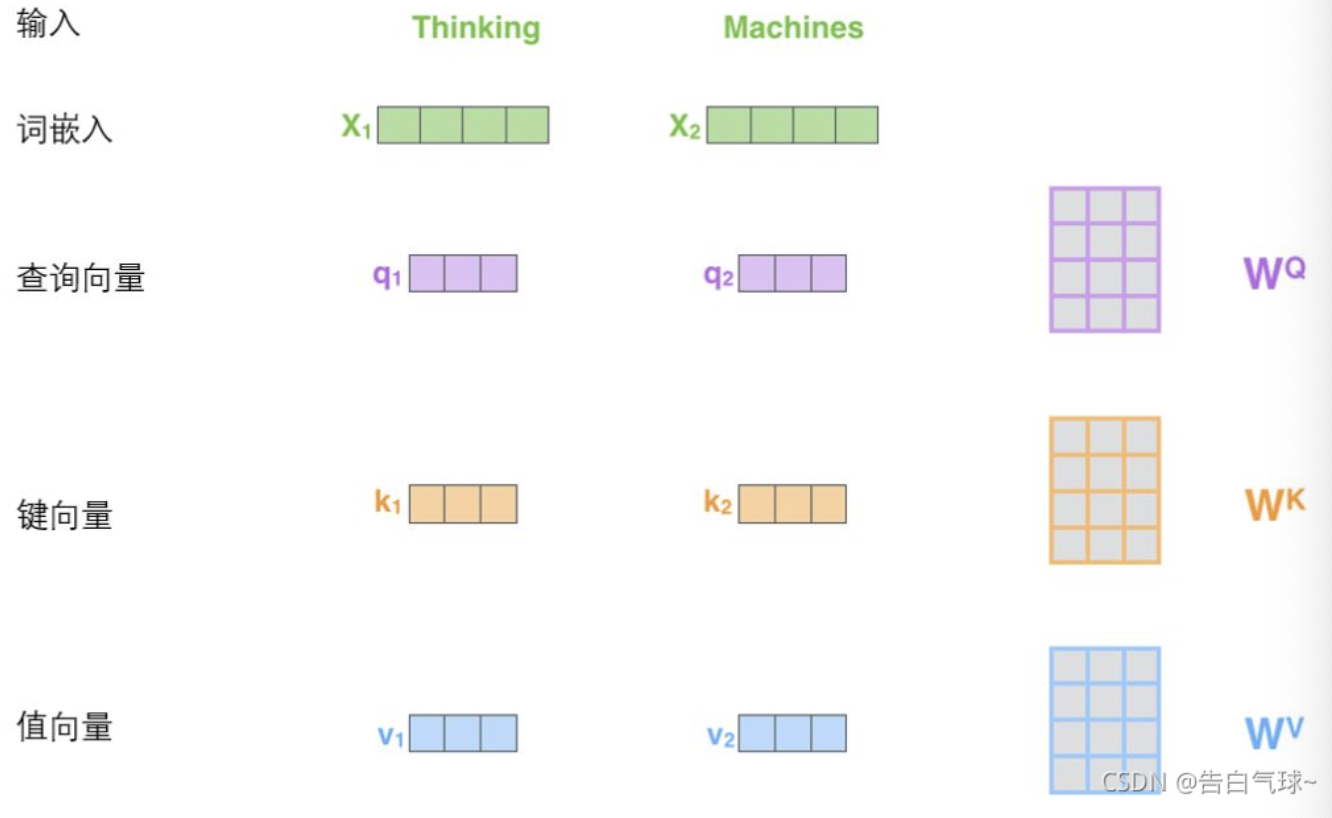
将单个向量组合,得到矩阵Q、K、V
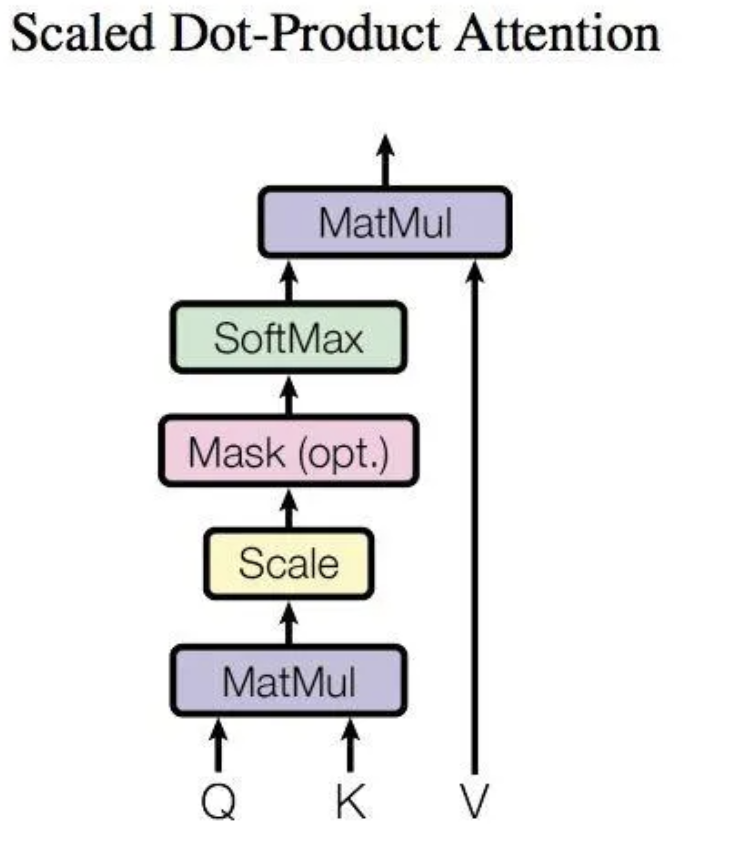
对于一个,计算自注意力向量时,需要所有x_j对x_i打分。即
, j取遍整个空间。
为了控制注意力分数的方差为1,确保在通过Softmax函数后能得到一个稳定、有效的概率分布,在计算完分数后要除以。即
3.2. multi-head attention
有多个查询/键/值权重矩阵集合,(Transformer使用八个注意力头)并且每一个都是随机初始化的。和上边一样,用矩阵X乘以WQ、WK、WV来产生查询、键、值矩阵。每组分别计算得到一个Z矩阵。
前馈层只需要一个矩阵,则把得到的8个矩阵拼接在一起,然后用一个附加的权重矩阵W_o与它们相乘。
3.3. 点积模型做放缩的原因
是为了控制注意力权重的尺度,以避免在计算过程中出现梯度爆炸的问题。
Attention的计算是在内积之后进行softmax,主要涉及的运算是,计算上溢,概率分布也会极端化。Softmax的输出几乎是一个one-hot向量(一个位置接近1,其余全部接近0)。这时,对于非最大值的位置,其梯度会非常小,接近于0,导致模型无法通过梯度下降进行有效学习。
为了解决方差增大的问题,一个经典的统计学方法就是进行缩放。在内积之后除以 d,使q⋅k的方差变为1
3.4. 在计算score时,如何对padding做mask操作
padding位置置为负无穷(一般来说-1000就可以),再对attention score进行想加。
为何不取0: ,不是0,计算会出现错误 ,而
3.5. transformer对并行化怎么理解?
层内并行:在Self-Attention层中,计算是按层进行的,而不是按时间步。输入的是所有词嵌入向量拼接成的大矩阵X[序列长度,模型纬度]。输出一次性得到所有词的输出向量。
3.6. MHA & MQA & MGA
3.6.1. MHA
模型共同关注来自不同位置的不同表示子空间的信息
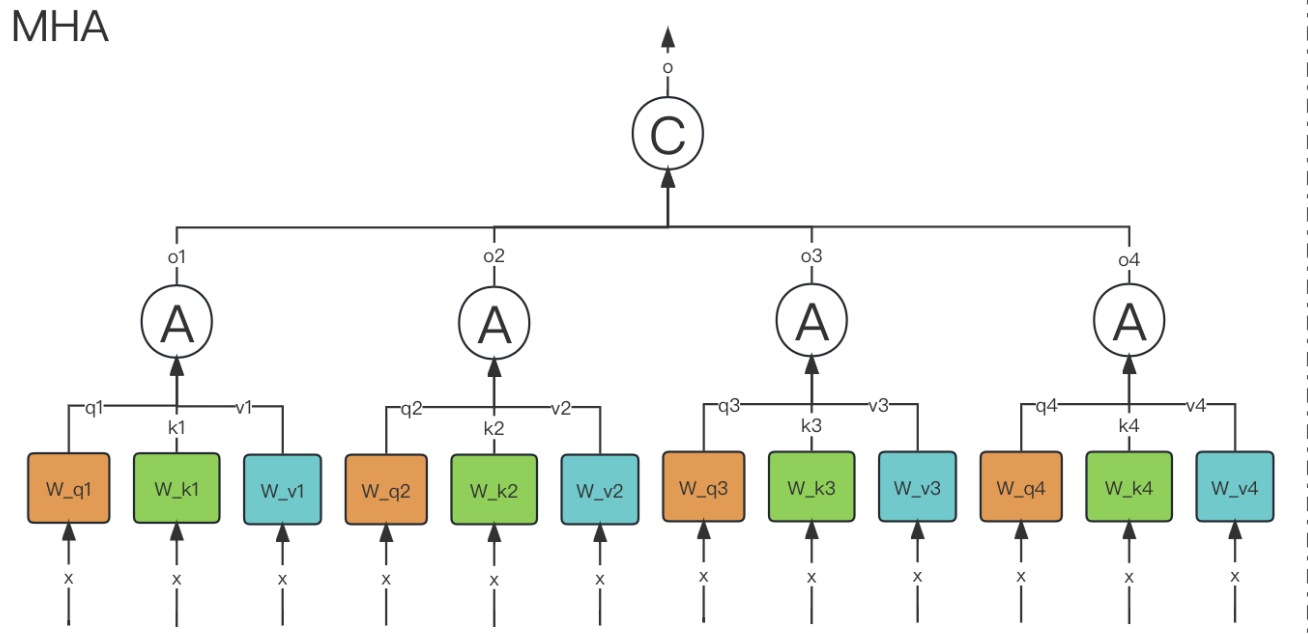
作用:能让每个注意力机制去优化每个词汇的不同特征部分,从而均衡同一种注意力机制可能产生的偏差,让词义拥有来自更多元的表达,实验表明可以从而提升模型效果.
代码实现:
import torch
from torch import nn
class MultiHeadAttention(nn.Module):
def __init__(self, hidden_size, num_heads):
super(MultiHeadAttention, self).__init__()
self.num_heads = num_heads
self.head_dim = hidden_size // num_heads
self.q_linear = nn.Linear(hidden_size, hidden_size)
self.k_linear = nn.Linear(hidden_size, hidden_size)
self.v_linear = nn.Linear(hidden_size, hidden_size)
self.o_linear = nn.Linear(hidden_size, hidden_size)
def split_heads(self, x):
batch_size = x.size(0)
# 先view再转置: [batch, seq_len, num_heads, head_dim] -> [batch, num_heads, seq_len, head_dim]
return x.view(batch_size,-1, self.num_heads, self.head_dim).transpose(1, 2)
def forward(self, hidden_states, attention_mask=None):
# hidden_state : [batch_size, seq_len, hidden_size]
# attention_mask: [batch_size, seq_len, hidden_size]
batch_size = hidden_states.size()[0]
# 与权重矩阵相乘
query = self.q_linear(hidden_states)
key = self.k_linear(hidden_states)
value = self.v_linear(hidden_states)
# 划分
query = query.view(batch_size, -1, self.num_heads, self.head_dim).transpose(1, 2)
key = key.view(batch_size, -1, self.num_heads, self.head_dim).transpose(1, 2)
value = value.view(batch_size, -1, self.num_heads, self.head_dim).transpose(1, 2)
# 计算分数
scores = torch.matmul(query, key.transpose(-1, -2)) / torch.sqrt(torch.tensor(self.head_dim, dtype=torch.float32))
if attention_mask is not None:
scores = scores + attention_mask * -1e-9
attention_weights = torch.softmax(scores, dim=-1)
output = torch.matmul(attention_weights, value)
# 拼接分数
# output[bs, nums_heads, seq_len, head_dim]
output = output.transpose(-1, -2).contiguous().view(batch_size, -1, self.num_heads*self.head_dim)
output = self.o_linear(output)
return output
if __name__ == '__main__':
batch_size = 2
seq_len = 10
hidden_size = 512
num_heads = 8
hidden_states = torch.randn(batch_size, seq_len, hidden_size)
print(f"输入形状: {hidden_states.shape}")
model = MultiHeadAttention(hidden_size, num_heads)
output = model(hidden_states, attention_mask=None)
print(output.shape)
3.6.2. MQA multi-query attention
MQA 让所有的头之间共享同一份 Key 和 Value 矩阵,每个头正常的只单独保留了一份 Query 参数,从而大大减少 Key 和 Value 矩阵的参数量。
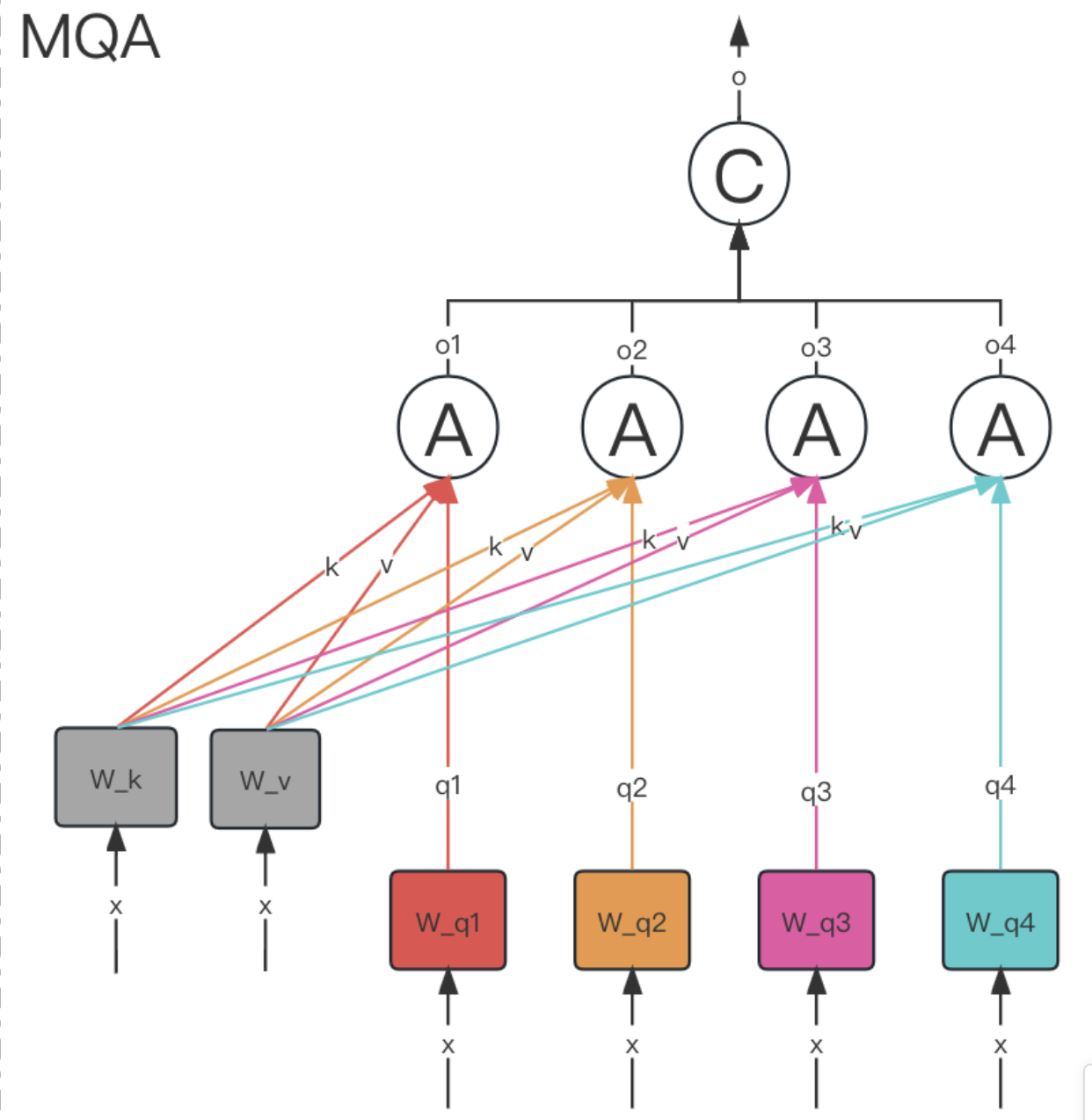
只会保留一个单独的key-value头,这样虽然可以提升推理的速度,但是会带来精度上的损失.
3.6.3. GQA
grouped query attention,会对 attention 进行分组操作,query 被分为 N 组,每个组共享一个 Key 和 Value 矩阵
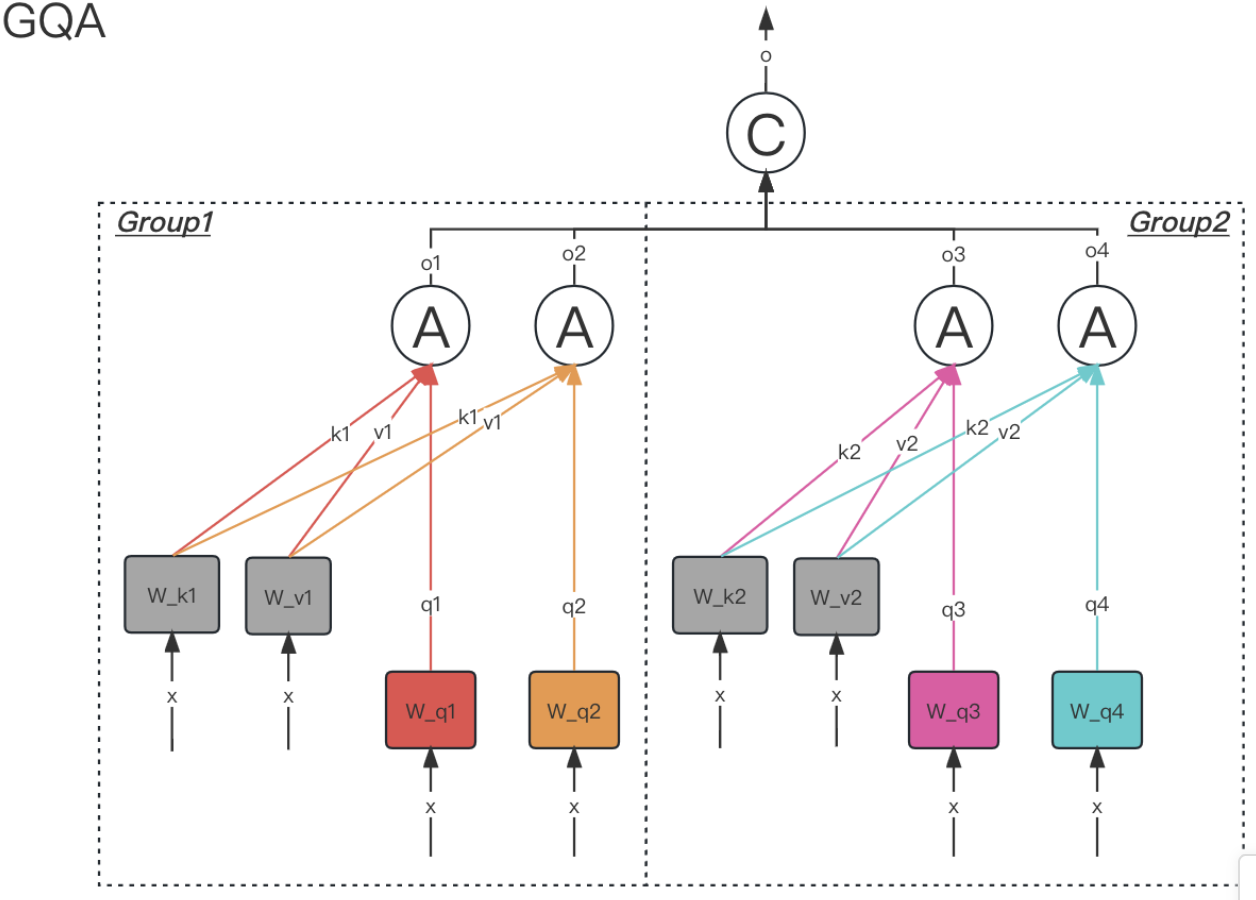
4. Add&Norm
- Add:加入残差块的目的是为了防止在深度神经网络的训练过程中发生退化的问题。
- Norm:归一化,LN是在同一个样本中不同神经元之间进行归一化。
4.1. 为什么残差连接能防止梯度消失和梯度爆炸?
在计算梯度的时候,
即使 第一项很小,但有了第二项,总体梯度至少为1
4.2. 为什么选用LN而不选择BN?
BN是在对batch纬度做归一化,LN是对特征纬度做归一化
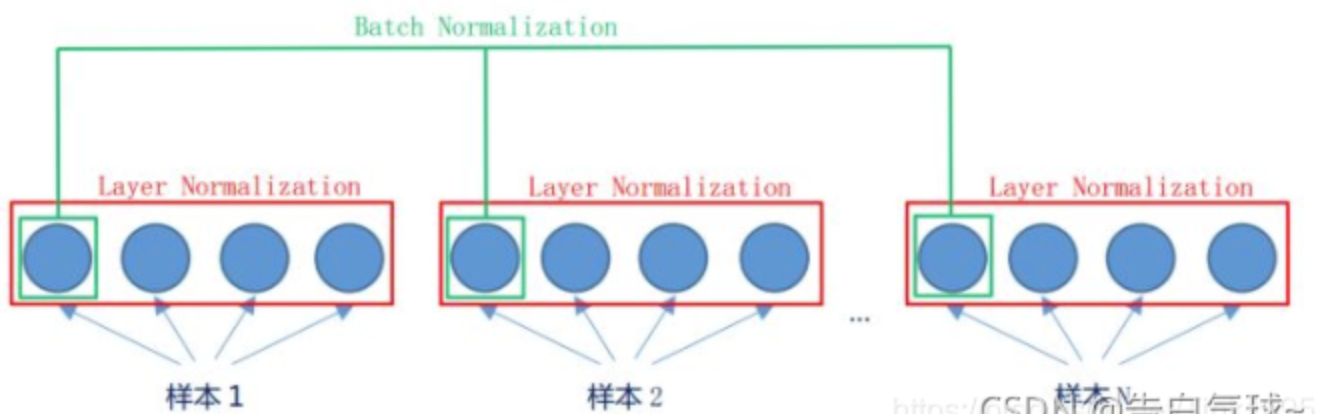
NLP中都是词向量,不同序列的长度可能差异很大,BN于短序列,某些位置的统计量可能基于很少的样本。单独分析它的每一维是没有意义的。BN更适合图像处理。
另外,在Transformer中,我们通常使用小batch训练,BN: 在每个特征维度上只有少量样本计算统计量 → 不稳定。























 3333
3333

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








