LeetCode 78. 子集（分治）-优快云博客

文章讨论了如何使用分治策略解决LeetCode中的子集问题，通过存储子集到set中避免重复，并利用erase方法动态删除数组元素。作者尝试使用unordered_set优化复杂度但遇到困难。另外，文章提到了官方题解中的位运算解决方案，指出子集数量与2的幂次关系，并解释如何通过位运算决定元素是否选入子集。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

LeetCode 78. 子集

原题
思路
代码
运行截图
收获

原题

LeetCode 78. 子集

思路

用分治的思想来做。
用set来存储子集。（本意是去重，但后来发现可以用find函数把可能存储的重复值去掉）
每次去掉一个元素，然后再分治下去。如果set里已经有了就不访问了。
最后把set里的元素push到ans里。

代码

class Solution {
public:
    set<vector<int>> s;
    void check(vector<int> nums) {
        int n = nums.size();
        s.insert(nums);
        if (n == 0) return;
        for (int i = 0; i < n; i++) {
            vector<int> subnums = nums;
            subnums.erase(subnums.begin()+i);
            if (s.find(subnums) == s.end())  check(subnums);
        }
    }
    vector<vector<int>> subsets(vector<int>& nums) {
        check(nums);
        vector<vector<int>> ans;
        for (auto it = s.begin(); it != s.end(); it++) ans.push_back(*it);
        return ans;
    }
};

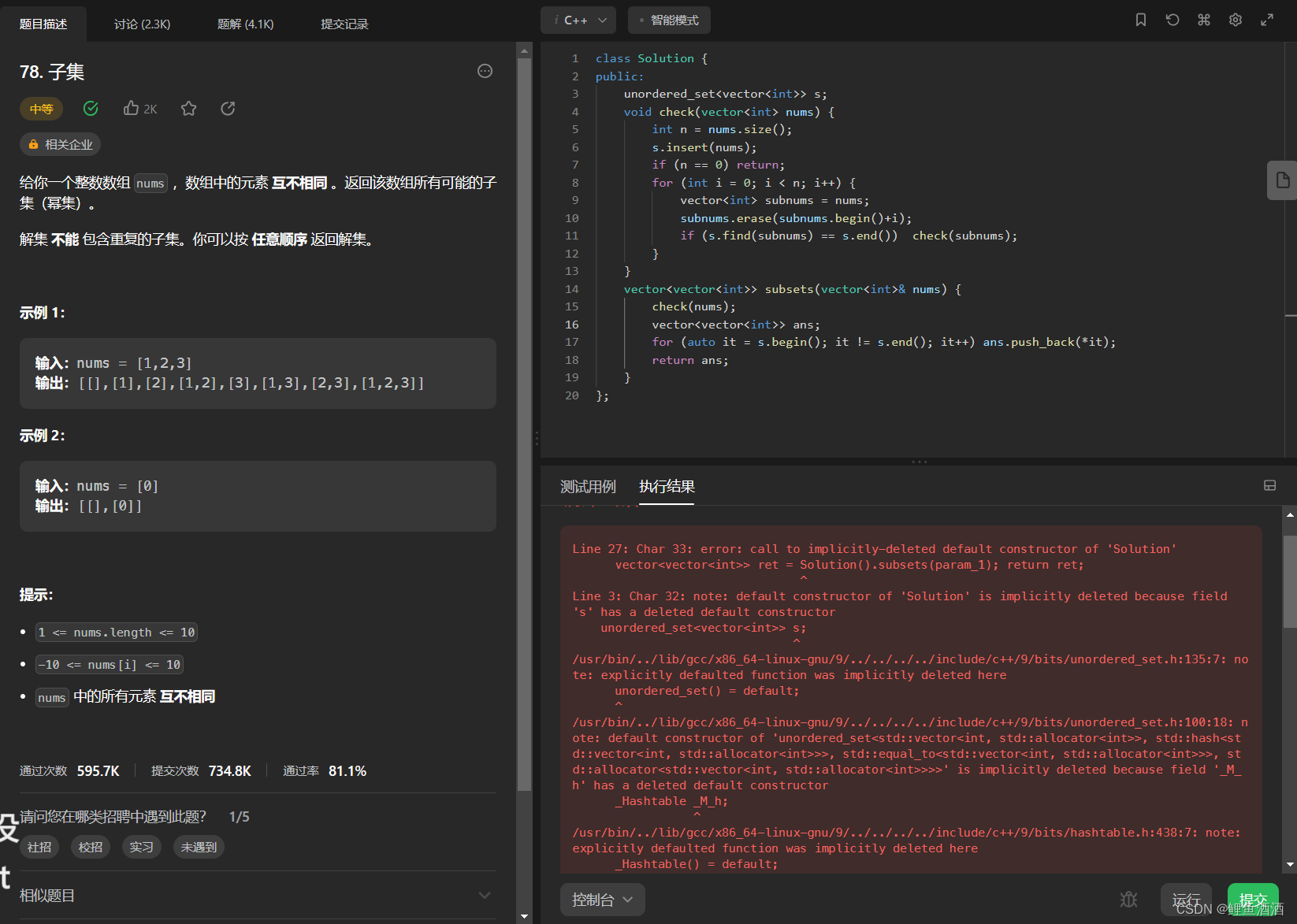
运行截图

在这里插入图片描述

收获

动态数组删除元素：erase(v.begin() + i)
当用分治或者递归超出时间限制的时候，想想在进入递归或者分治的条件处可以去除掉一些重复的递归。
这里的set我本来在想能不能用unordered_set来降一些复杂度。但是出现了一些错误，暂时没找到解决办法。
官方题解位运算。子集的数量是2的n次方。其中位运算中（1<<n）的值就是2的n次方-1。而每个状态对应子集的构建其实就是 选与不选，也就是0/1的区别。所以通过一个n的遍历，由mask & （1<<i）来决定该状体里此值是否被选进动态数组里。位运算的精妙…