2020春大连理工概率统计 上机作业

---

文首提示

如果有校友同学看到，这个作业都是随机数，自己用R语言ide再写一遍，千万别直接照抄，数都是随机的！！！！！！

第一次上机作业

1.（a）

> a <- rnorm(1000)
> mean(a)
[1] 0.03495309
> var(a)
[1] 0.9732954

（b）

> hist(a,freq=F)

期望很接近0，直方图的峰值在0的附近，左右分布较为均匀；
方差很接近1 。与计算结果较为拟合

2.（a）

> x <- rpois(100,2)
> mean(x)
[1] 1.93
> var(x)
[1] 1.964747
> hist(x,freq=F)
 

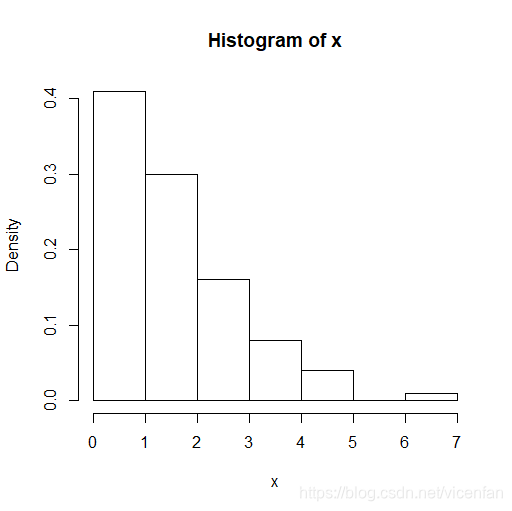
（b）

> y = seq(1,1000,1)
> for(i in 1:1000){
+ x <- rpois(100,2)
+ y[i] <- (mean(x))
+ }

（c）

> sy = seq(1,1000,1)
> for(i in 1:1000){
+ sy[i] <- ((y[i]-2)/sqrt(2/100))
+ }
> mean(sy)
[1] 0.01944544
> var(sy)
[1] 0.9973142

（d）

> hist(sy,freq=F)

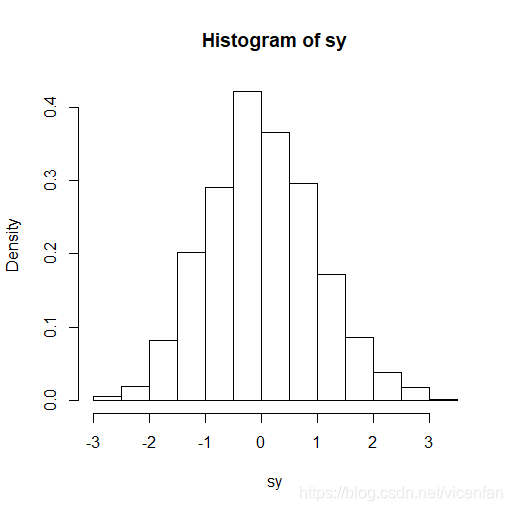
将sy的直方图与第一题相比，可以看出两者较为相似：峰值在0的附近，左右分布较为均匀。证明了当重复次数较大时，泊松分布可以用正态分布来代替。

第二次上机作业

> x = runif(1000,5,10)
> y = 4*x-6
> mean(x)
[1] 7.503603
> mean(y)
[1] 24.01441

> var(x)
[1] 2.11572
> var(y)
[1] 33.85152
> cov(x,y)
[1] 8.462881
> cor(x,y)
[1] 1

n=1时：

> y = x*exp(2*(x^(0)))
> cor(x,y)
[1] 1

n=2时：

> y = x*exp(2*(x^(1)))
> cor(x,y)
[1] 0.6700377

n=3时：

> y = x*exp(2*(x^(2)))
> cor(x,y)
[1] 0.1511285

随着n的增大，X和Y的相关系数在变小。
随着n的增大，y的方差越来越大，x，y的协方差越来越大，所以相关系数越来越小。