NBUOJ 1461 求和号(数学，推公式)

Description

在数学运算中经常要计算连续的和，例如，计算1+2+3+…+n，或者等比数列a+a2+…+an。我们经常使用求和号“∑”来表示这类连续的和。通常在∑的下方标上自变量名称和初始值，在∑的上方标终止值，而在∑的右方写表达式，如：

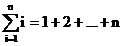
求和号也可以嵌套使用，如：

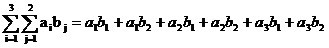
现在请计算

Input

第一行有两个整数，表示n和m。以下从第2行到第n+1行，每行包含一个整数，依次表示ai的值。紧接着从第n+2行到第n+m+1行，每行包含一个整数，依次表示bj的值。每个文件只包含一组测试数据。

Output

对每组测试数据输出一行，仅包含一个整数，即计算得到的结果。

Sample Input

2 3
1
2
4
6
8

Sample Output

54

HINT

数据范围：1<=n,m<=100 000，所给出的ai，bj的绝对值<=10 000。

注意时间限制。

考察点

公式求值

注意点

要先做好公式推导的工作，如果直接按照原始的公式计算，乘法次数容易超时

公式推导

源码

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;

typedef long long ll;
int main()
{
	ll sum1,sum2,n,m,i,tp;
	while(scanf("%lld%lld",&n,&m)!=EOF)
	{
		sum1=sum2=0;
		for(i=0;i<n;i++)
		{
			scanf("%lld",&tp);
			sum1+=tp;
		}
		for(i=0;i<m;i++)
		{
			scanf("%lld",&tp);
			sum2+=tp;
		}
		printf("%lld\n",sum1*sum2);
	}
	return 0;
}