本文深入探讨了算法的时间复杂度，包括常数阶O(1)、线性阶O(n)、对数阶O(logn)及平方阶O(n^2)等不同级别的复杂度概念与实例。通过具体案例解释了每种复杂度的特点及其在编程中的应用。
算法的时间复杂度为语句总的执行次数，记作T(n) = O(f(n)) 是关于问题规模n的函数。
常数阶O(1)：顺序结构，分支结构
语句的运行次数x与n无关, 无论运行多少次，都是O（1）的时间复杂度。
e.g.
线性阶O(n):一个循环
运行次数与n成正比
e.g.
int i;
for(i = 0; i < n: i++)对数阶O（logn）:二分查找
x记为运行次数
平方阶O(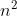
): 循环嵌套
P.S.常见的时间复杂度
算法面试笔记: 计算算法时间复杂度
最新推荐文章于 2022-04-17 22:52:52 发布
扫一扫
932
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
