玩儿转算法面试Chapter2_时间复杂度分析

Section 1

随着算法规模n的增大，常数项系数的影响并不那么大，甚至可以忽略。

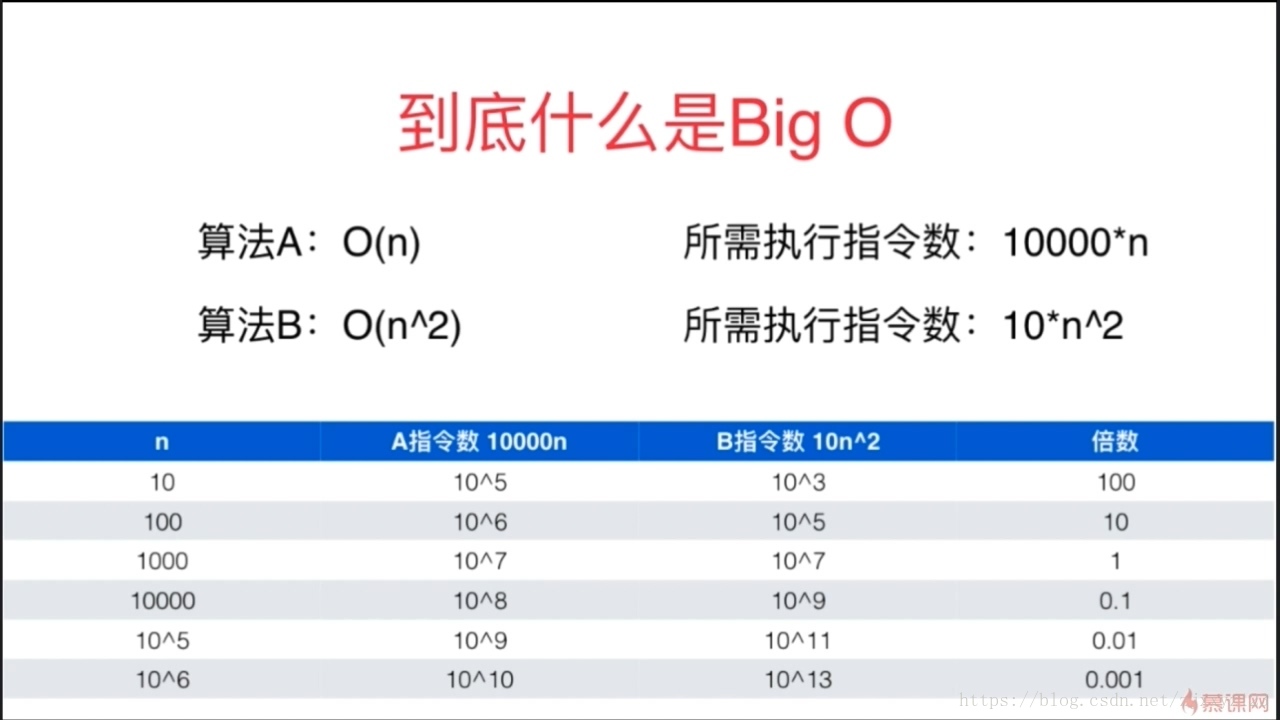
由上可知，时间复杂度衡量的是一个量级上的东西，当N超过一个点时，时间复杂度低的算法一定比时间复杂度高的算法执行慢。而我们研究的一般是大规模数据，因为对于小规模数据，研究算法其实没什么意思，比如排序，当N小于一个值时，便使用插入排序。

以上是针对数据规模一样的情况，可以选取量级大的那个代表整个算法的时间复杂度。但当两部分数据规模不一致时：

举例，时间复杂度分析时数据规模不一致的例子：


注意：为什么将整个字符串数组按照字典序排序时时间复杂度为O(s*nlogn),因为排序的时间复杂度是指 比较执行的次数为 O(NlogN)级别的，而假设每一个字符串含有s个字符，那么按照字典序排序，比较的次数自然便是 O(s*nlogn)

关于算法的用例相关，但是我们还是关注的是平均情况

Section 2

为了保险起见，以上数据规模除以10也可以。
有了以上对于数据规模与时间复杂度的概念，那么根据给定的数据规模，就可以帮助我们在面试中选择合适的算法。

O(1)的空间复杂度说明，所开的空间也数据规模 N 无关，是固定的空间大小。
当我们进行递归调用时，系统将我们递归前的状态压入栈中的。
递归的深度是会影响相应空间复杂度。。

Section 3：常见的复杂度分析

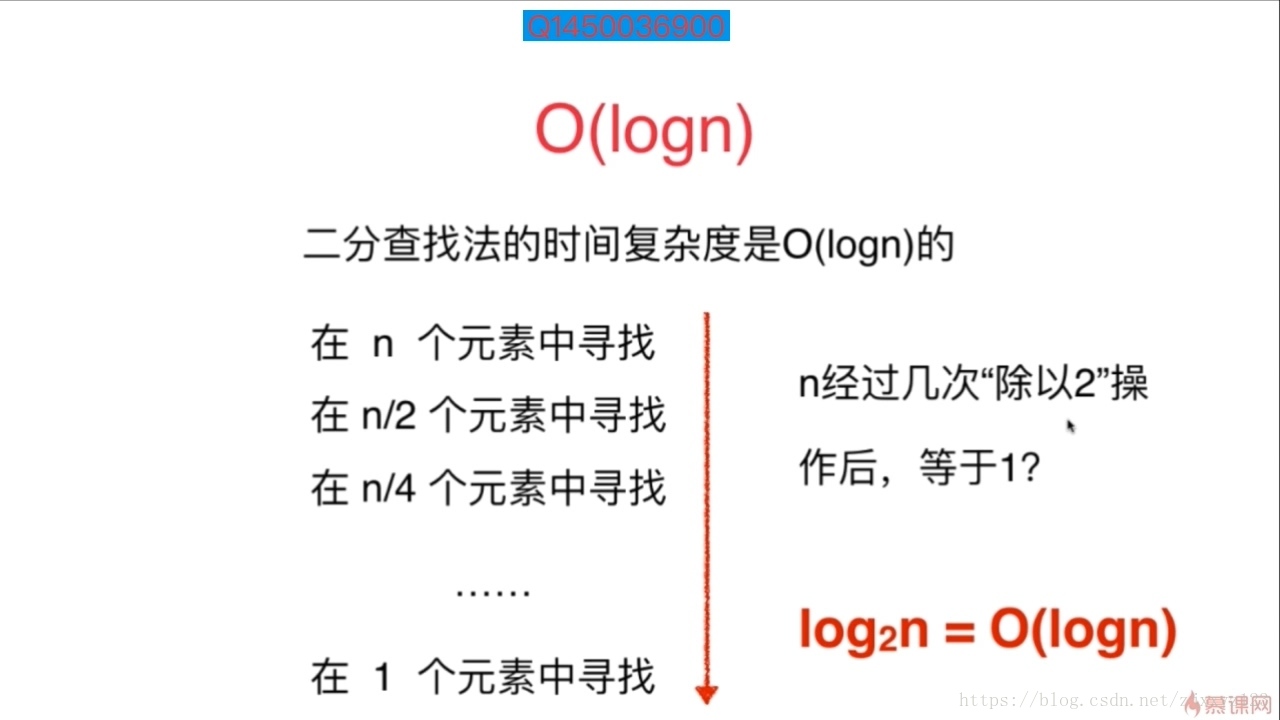
所以，如果是求 N 除以一个数 a ,最后等于 1 ，那么这就是一个O(logN)级别的时间复杂度问题。


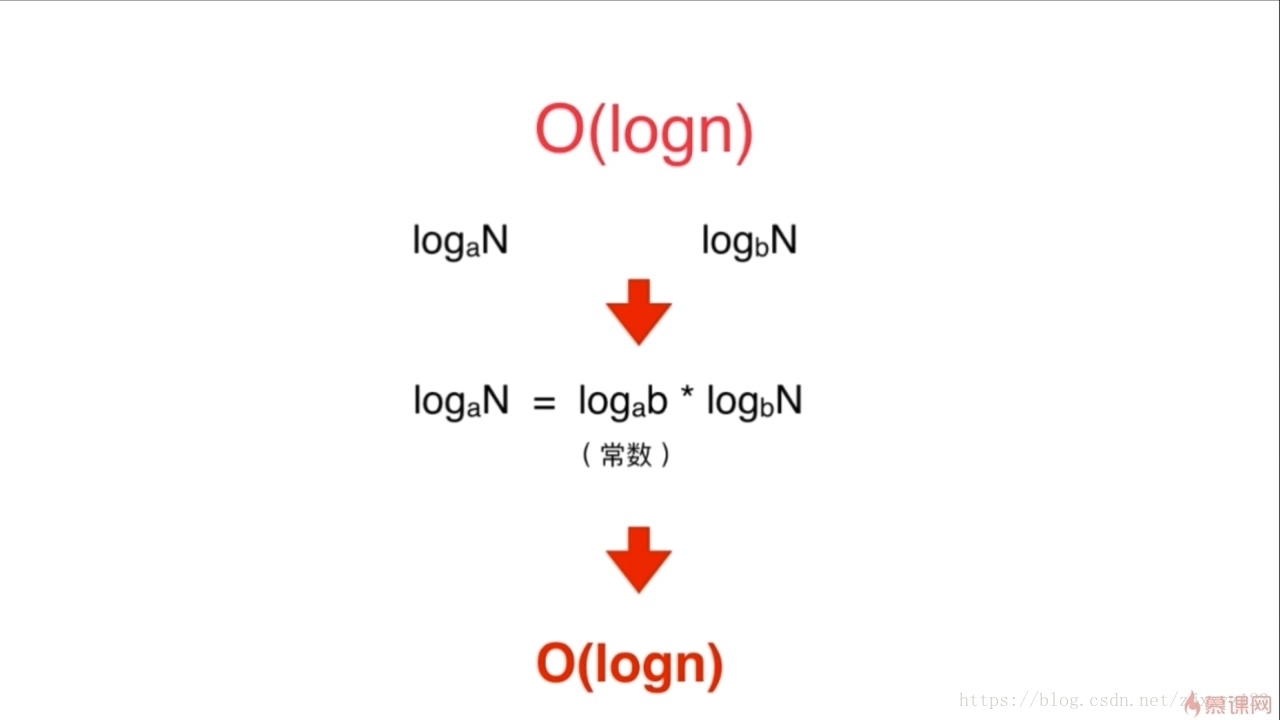
所以，不管对数底为多少，统一忽略底，视为O(logN)的时间复杂度。
举几个陷阱例子：

这个例子里层循环时O(N)次，但对于外层循环，注意增量的变化，是 1，2，4…..n这样变化的，那么外层执行的次数是 n 经过多少次 除以2 操作后，变成了1，所以是 O(log n),综合来看，这个算法时间复杂度为 O(NlogN)。
所以，分析时间复杂度，要关注循环的起始点，终止点，最重要的是增量的变化。

以上判断一个数是否为素数的算法，便是循环的终止条件决定了复杂度。

Section 4

为了保险起见，也可以降一个数量级
通过实验验证你的程序的复杂度。

Section 5:递归算法的复杂度分析

总结：

T:为当前递归函数中，除了调用递归以外，其他操作所带来的时间复杂度。也可以这样理解，每一次递归带来的时间复杂度为 O(T),那么进行 depth次递归，整体的复杂度自然便是 O(T*depth)。


因为以上每个递归函数内只会最多进行一次递归，b那么递归的深度便是递归的次数。
而对于递归中多次进行递归的情况，必须考虑的是递归的次数，可以借助于递归树的形式去思考此类问题


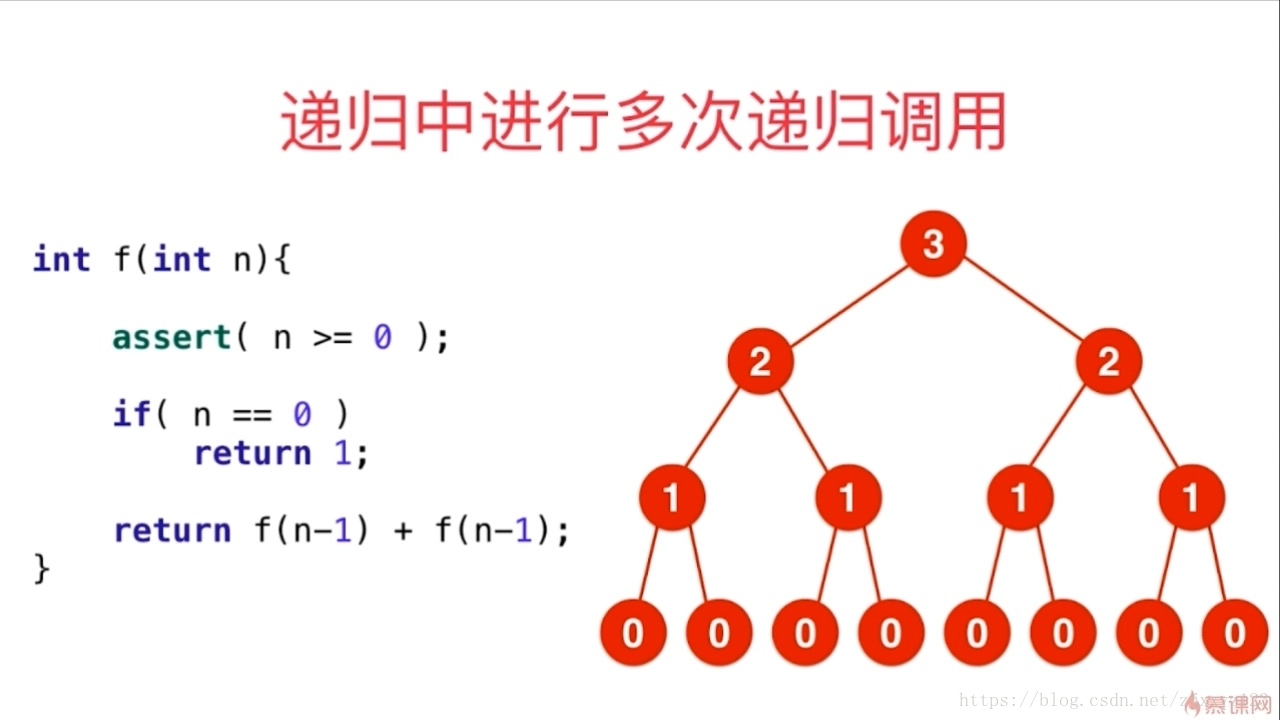
数递归树的节点即可。


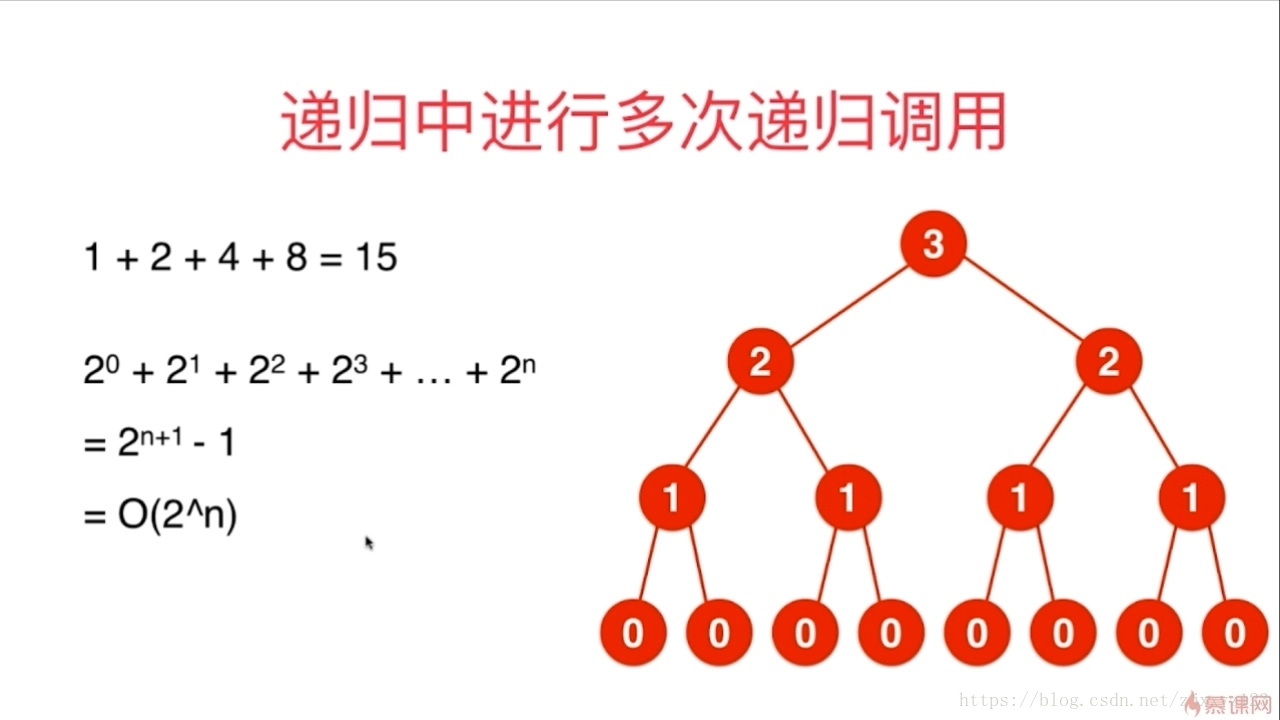
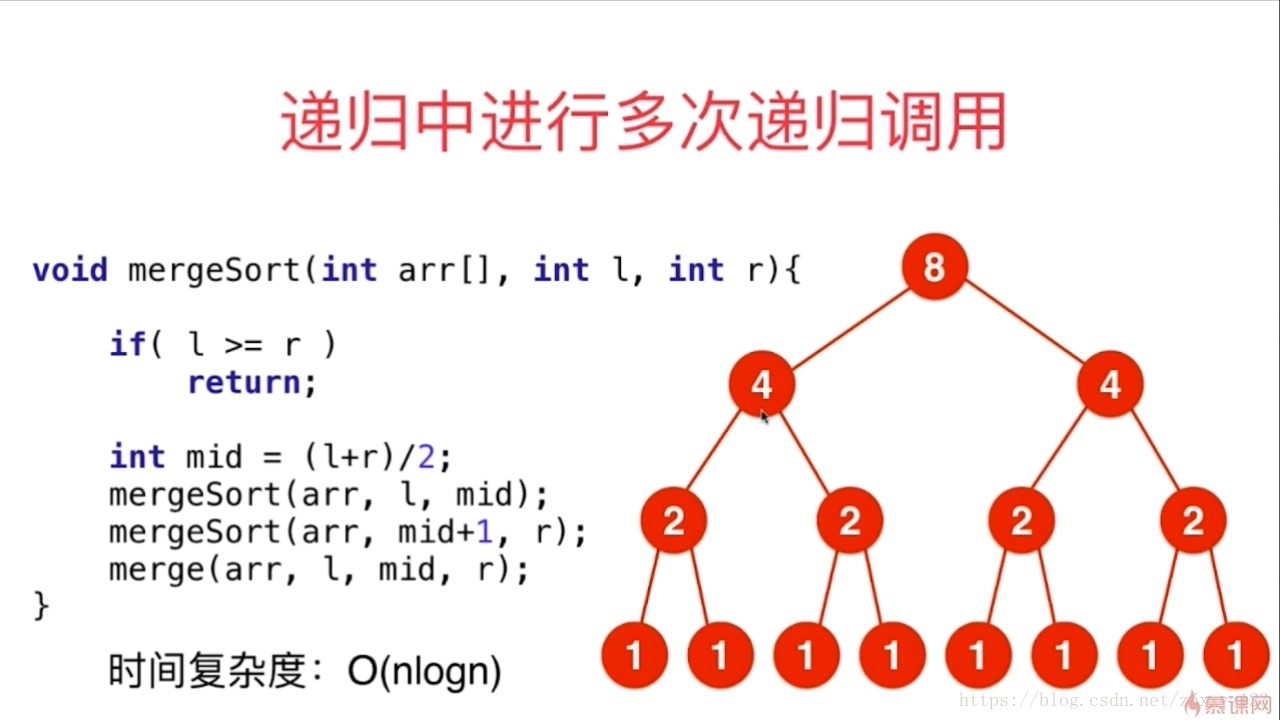
对于归并排序，可以这样想，每一次递归排序都要遍历全部N个元素，为O(N),然后要进行logN次的归并排序，所以时间复杂度为O(NlogN)
空间复杂度为O(N+logN),因为归并操作需要O(N)的额外空间和logN的栈空间（递归深度）
对于递归更复杂的情况：

Section 6: 均摊复杂度分析

• 拿向动态数组里push举例：
  
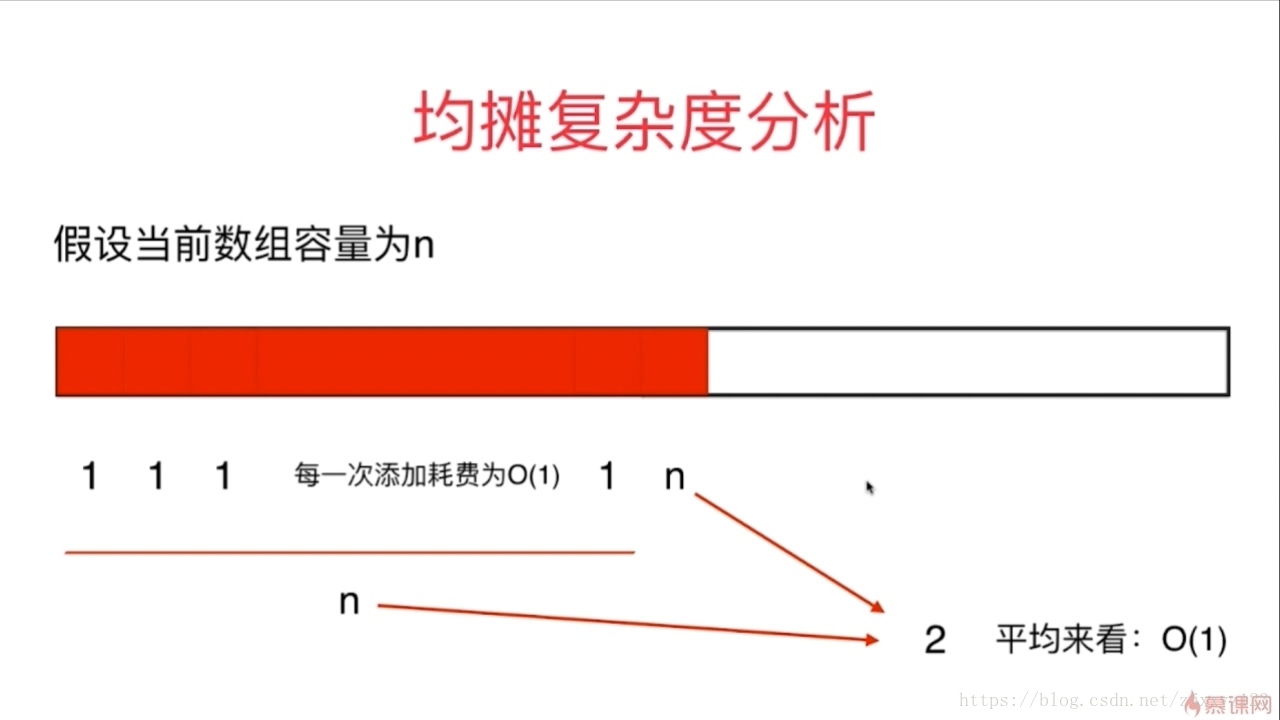
  未超过capcity时，push操作为O(1),然后超过capcity时，扩容，此时复杂度为O(N),但均摊到这一段数字是，复杂度依然是O(1),这便是均摊复杂度
  
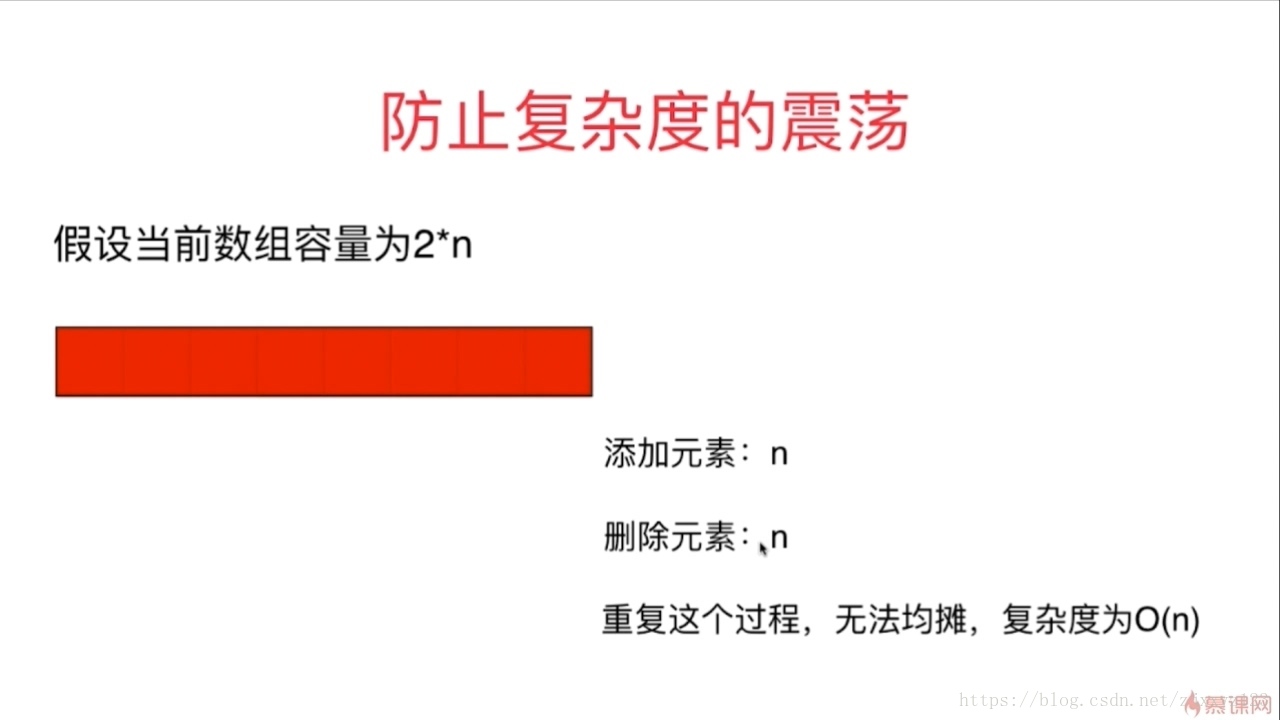
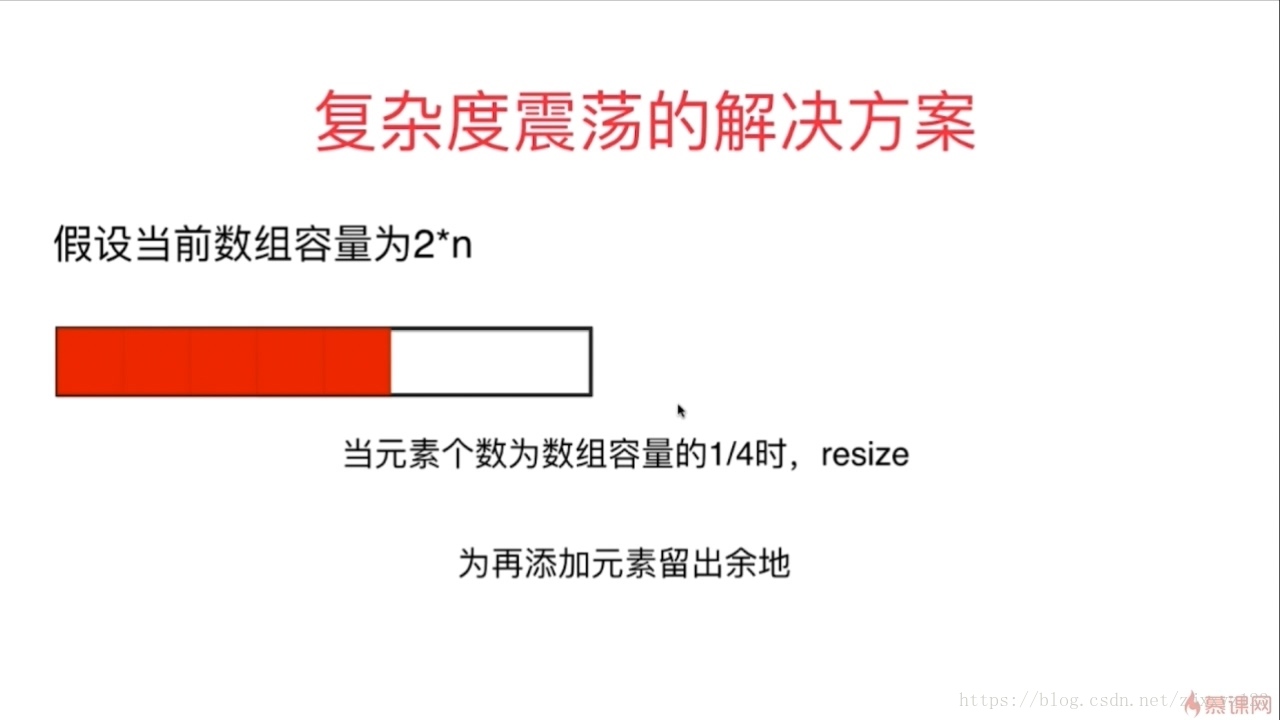
  若同样在size小于Capcity时，释放一半空间，那么会引发复杂度震荡问题。不断在边界点处删除添加，便会不断扩容，释放，造成O(N)的时间复杂度。