【深度学习中的损失函数整理与总结】

介绍

损失函数在机器学习或深度学习中非常重要，假设您正在处理任何问题，并且您已经在数据集上训练了一个机器学习模型，并准备将其放在您的客户面前，但是你怎么能确定这个模型会给出最佳结果呢？是否有指标或技术可以帮助您快速评估数据集上的模型？

是的，这里损失函数在机器学习或深度学习中就发挥了重要的作用。

在本文中，我整理并总结了不同类型的损失函数。

什么是损失函数？

维基百科说，在数学优化和决策理论中，损失或成本函数（有时也称为误差函数） 是将事件或一个或多个变量的值映射到一个实数上的函数，该实数直观地表示了本事件。
简单来说，损失函数是一种评估算法对数据集建模效果的方法，它是机器学习算法参数的数学函数。

为什么损失函数很重要？

著名作家彼得·德鲁克 (Peter Druker) 说：你无法改进你无法衡量的东西。这就是为什么要使用损失函数来评估您的算法对数据集建模的效果。如果损失函数的值较低，那么它是一个好的模型，否则，我们必须改变模型的参数并最小化损失。

损失函数与成本函数

大多数人混淆了损失函数和成本函数，让我们了解什么是“损失函数”和“成本函数”。成本函数和损失函数是同义词，可以互换使用，但它们是不同的。

损失函数：

损失函数/误差函数用于单个训练示例/输入。

成本函数：

成本函数是整个训练数据集的平均损失。

深度学习中的损失函数

1. 回归
   MSE（均方误差）
   MAE（平均绝对误差）
   哈伯损失

2. 分类
   二元交叉熵
   分类交叉熵

3. 自动编码器
   KL 散度

4. GAN
   鉴别器损失
   Minmax GAN 损失

5. 物体检测
   焦点损失

6. 词嵌入
   三重损失

在本文中，我们将了解回归损失和分类损失。

A. 回归损失

1. 均方误差/平方损失/L2 损失

均方误差 (MSE) 是最简单和最常见的损失函数，要计算 MSE，您需要获取实际值和模型预测值之间的差异，对其进行平方，然后在整个数据集上对其进行平均。

优点

1. 易于解释。
2. 总是因方而微分。
3. 只有一个局部最小值。

缺点

1. 方格中的误差单位。因为没有正确理解广场中的单位。

2. 对异常值不稳健

   注意：在最后一个神经元的回归中使用线性激活函数。

2. 平均绝对误差/L1 损失

平均绝对误差（MAE）也是最简单的损失函数，要计算 MAE，您需要获取实际值和模型预测值之间的差异，然后在整个数据集中对其进行平均。

优点

1. 直观简单
2. Error Unit 与输出列相同。
3. 对异常值具有鲁棒性

缺点

1. 不能直接使用梯度下降，可以进行次梯度计算。
   注意：在最后一个神经元的回归中使用线性激活函数。

3. 胡伯损失

在统计学中，Huber 损失是一种用于稳健回归的损失函数，它对数据中的异常值的敏感性低于平方误差损失。

n——数据点的数量。
y——数据点的实际值，也称为真值。
ŷ——数据点的预测值，该值由模型返回。
δ——定义 Huber 损失函数从二次型转变为线性的点。

优点

1. 对异常值具有鲁棒性
2. 它位于MAE和MSE之间。

缺点

1. 它的主要缺点是关联复杂度，为了最大限度地提高模型精度，还需要优化超参数 δ，这会增加训练的要求。

B. 分类损失

1. 二元交叉熵/对数损失

它用于像两个类这样的二元分类问题，例如，一个人是否感染了新冠病毒，或者我的文章是否受欢迎。
二元交叉熵将每个预测概率值，可能是 0 或 1 ，与实际类输出进行比较。然后它根据与期望值的距离计算惩罚概率的分数，这意味着离实际值有多近或多远。

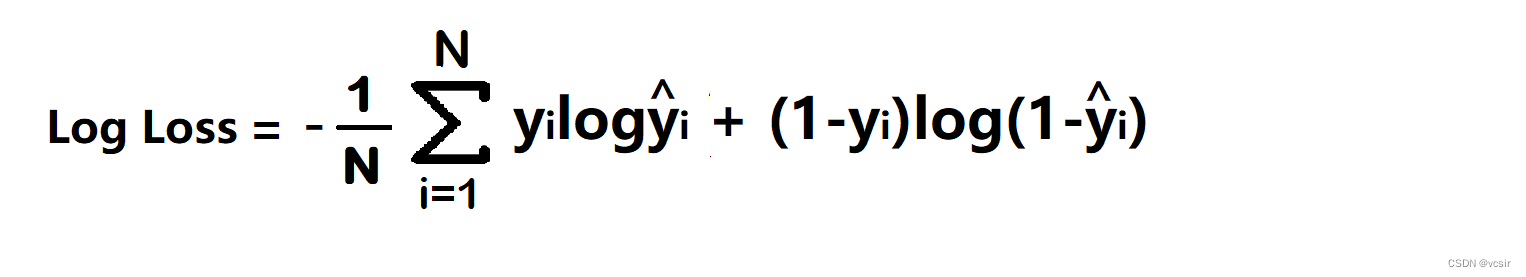
yi——实际值
yi^——神经网络预测值

优点

1. 成本函数是微分函数。

缺点

1. 多个局部最小值
2. 不直观

注意 ：在最后一个神经元的分类中使用 sigmoid 激活函数。

2. 分类交叉熵

分类交叉熵用于多类分类问题，也用于 softmax 回归。

注意：在最后一个神经元的多类分类中使用 softmax 激活函数。

何时使用分类交叉熵和稀疏分类交叉熵？

如果目标列为 0 0 1、0 1 0、1 0 0 等类似的热编码，则使用分类交叉熵。如果目标列为 1,2,3,4….n 等类似的数字编码，则使用稀疏分类交叉熵。

哪个更快？

稀疏分类交叉熵比分类交叉熵快。

结论

在本文中，我主要整理并总结了深度学习中不同类型的损失函数供大家参考和学习，若有不正确的地方，还请大家指正，谢谢！