计算机图形MVP变换

在Maple 2024下实现的立方体 模型视图投影变换

代码如下

displayCube := proc(rMat, title) 
	local i, j, p1, p2, p1v, p2v, x0, x1, y0, y1;
	local points :=Array([]);
	for i to 12 do
		for j to 3 do
			p1 := indicesVal[i,j];
			p2 := indicesVal[i, irem(j,3)+1 ];
			
			p1v := rMat[p1, 1..-1];
			p2v := rMat[p2, 1..-1];
			
			x0:= round(p1v[1]); y0:= round(p1v[2]);
			x1:= round(p2v[1]); y1:= round(p2v[2]);

			ArrayTools:-Append(points, [ [x0,y0], [x1,y1] ]);
			
		end do;
	end do;

	plot(points, axes=NONE, caption=title);
end;

# 定义模型, 行向量
cube := Matrix( [
		[1.000000, 1.000000, -1.000000],
		[1.000000, -1.000000, -1.000000],
		[1.000000, 1.000000, 1.000000],
		[1.000000, -1.000000, 1.000000],
		[-1.000000, 1.000000, -1.000000],
		[-1.000000, -1.000000, -1.000000],
		[-1.000000, 1.000000, 1.000000],
		[-1.000000, -1.000000, 1.000000]
]);

indicesVal := Array( [
[ 5, 3, 1 ],
[ 3, 8, 4 ],
[ 7, 6, 8 ],
[ 2, 8, 6 ],
[ 1, 4, 2 ],
[ 5, 2, 6 ],
[ 5, 7, 3 ],
[ 3, 7, 8 ],
[ 7, 5, 6 ],
[ 2, 4, 8 ],
[ 1, 3, 4 ],
[ 5, 1, 2 ]
] );


# 模型变换 -------------------------
rotateX := Matrix( [
	[1,0,0],
	[0, cos(rx * Pi / 180), -sin(rx * Pi / 180) ],
	[0, sin(rx * Pi / 180),  cos(rx * Pi / 180) ]
]);

rotateY := Matrix( [
	[ cos(ry * Pi / 180), 0, sin(ry * Pi / 180)],
	[0,1,0 ],
	[-sin(ry * Pi / 180), 0, cos(ry * Pi / 180)]
]);

rotateZ := Matrix( [
	[ cos(rz * Pi / 180), -sin(rz * Pi / 180), 0],
	[ sin(rz * Pi / 180),  cos(rz * Pi / 180), 0],
	[0,0,1]
]);

# 缩放矩阵
scaleXYZ := Matrix([
	[ 10, 0, 0 ],
	[ 0 , 10,0 ],
	[ 0 , 0, 10]
]);

modelTransMatrix := cube.rotateX.rotateY.rotateZ.scaleXYZ ;

objMat1 := evalf( eval(modelTransMatrix, [
	sx = 10, sy = 10, sz = 10,
	rx = 45, ry = 45, rz = 45 ]));

displayCube(objMat1, "模型变换");


# 视图变换 -------------------------
worldO := <0 , 0 , 0> ;
cameraO := <100 , 100 , 100> ;
cameraZ := LinearAlgebra:-Normalize( worldO-cameraO ,Euclidean,conjugate=false );
cameraX := LinearAlgebra:-CrossProduct( <0 , 1 , 0>, cameraZ );
cameraY := LinearAlgebra:-CrossProduct(  cameraZ, cameraX);

# 三个基向量组成矩阵
cameraMatrix := <
	cameraX | cameraY | cameraZ
>;


objMat2 := objMat1.(LinearAlgebra:-MatrixInverse(cameraMatrix ));
displayCube(objMat2, "视图变换");


# 正投影变换 -------------------------
minX := min(LinearAlgebra:-Column(objMat2,1));
maxX := max(LinearAlgebra:-Column(objMat2,1));
minY := min(LinearAlgebra:-Column(objMat2,2));
maxY := max(LinearAlgebra:-Column(objMat2,2));
minZ := min(LinearAlgebra:-Column(objMat2,3));
maxZ := max(LinearAlgebra:-Column(objMat2,3));

# 缩小到[-1,1]
OrthoProjection := Matrix([
	[2/(maxX-minX),	0,				0				],
	[0,				2/(maxY-minY),	0				],
	[0,				0,				2/(maxZ-minZ)	]
]);

objMat3 := evalf(objMat2.OrthoProjection.scaleXYZ);
displayCube(objMat3, "正交变换");

# 透视投影变换 -------------------------
R := cameraO[3]; 
d := 60; # 投影平面

for i to 8 do
	objMat3[i, 1] := objMat3[i, 1] * d / (R-objMat3[i, 3]);
	objMat3[i, 2] := objMat3[i, 2] * d / (R-objMat3[i, 3]);
	objMat3[i, 3] := objMat3[i, 3] * d / (R-objMat3[i, 3]);
end do;

objMat4 := evalf(objMat3.scaleXYZ);
displayCube(objMat4, "投影变换");

在Maple 2024下运行如图

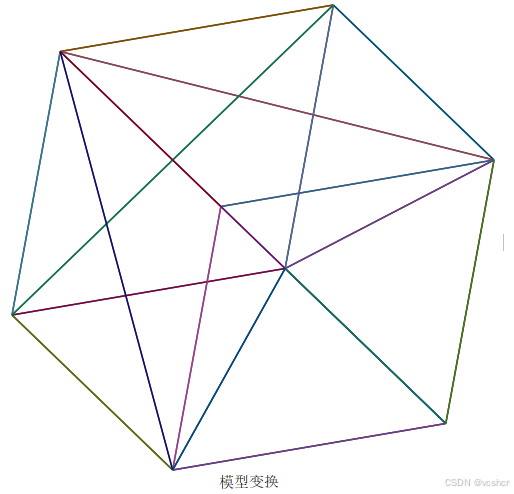
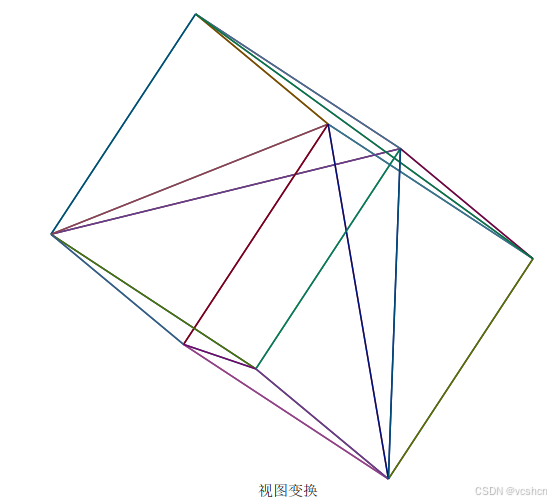
模型变换矩阵