【剑指offer题解整理版】树

最新推荐文章于 2021-11-24 22:30:45 发布

原创

最新推荐文章于 2021-11-24 22:30:45 发布 · 置顶 · 1.2k 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#binary tree

本文深入探讨了树的相关概念和算法，包括树的下一个结点、对称二叉树、镜像二叉树、多行打印二叉树、按之字形顺序打印、从上往下打印、序列化与反序列化、二叉树中和为某一值的路径、二叉树的深度、二叉搜索树的第k个结点以及二叉搜索树与双向链表的转换。文章通过实例分析和代码实现，详细解释了各种操作的逻辑和方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

树

考察点

树的数据结构特性

树的遍历规律、遍历序列特点: 树的下一个结点
树与递归: 对称二叉树、镜像二叉树
树与层序遍历：把二叉树打印成多行、按之字打印二叉树、序列化和反序列化二叉树、从上往下打印二叉树
二叉树与路径：二叉树中和为某一值的路径
二叉树与深度：二叉树的深度
二叉搜索树：二叉搜索树的第k个结点、二叉搜索树与双向链表

树的下一个结点

从树的中序遍历的规则分析一下，树的下一结点分几种情况？跟什么有关？

树的中序遍历序列的每一个part都遵循左根右(忽略空子树)的顺序规则。

由此可得出一个大致的结论，next结点要么与右子树有关，要么与根结点有关。

下面我们借助几个实例具体分析一下求树的下一个结点的问题，我们设想几种情况，先考虑最简化的情况，一个二层的二叉树：

pNode为根节点，那么当它右子树不为空时，下一结点为右子树为右子树的最左叶结点，当右子树为空时，next结点为空。
pNode为根的左结点时，next结点为父结点
pNode为根的右结点时，next结点为空。

进一步，考虑较为复杂的情况，一个三层的二叉树：

pNode为根节点，那么当它右子树不为空时，下一结点为右子树为右子树的最左叶结点，当右子树为空时，next结点为空。
pNode是父结点的左孩子时，next结点为父结点。
pNode是父结点的右孩子时，next结点为：

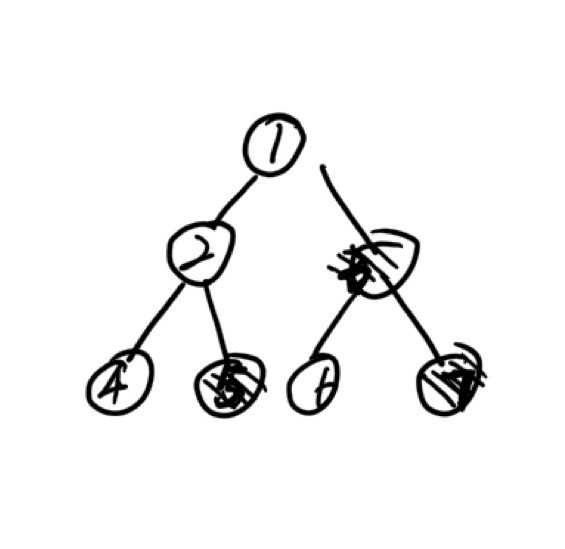
- 如pNode有右子树，那么next结点为右子树的最左叶节点
- 如pNode没有右子树，那么next结点分两种情况:
    - 父节点的父结点为空，next结点为空(如图中结点3的情况)。 
    - 父节点是它父节点的左孩子，next结点为祖父结点(如图中结点5的情况)
    - pNode的父亲结点是其父节点的右孩子，那么next结点为空(如途中结点7的情况)。

对于三层的二叉树的分析已经接近一般性的二叉树了，我们再自己分析一下就可以推断出，对于更多层数的二叉树也是这样的。
此外，我们可以继续简化上述的规律，我们发现处理情况1和情况3的规则几乎是一样的，因此可以合并一下：
next结点只与右子树、父结点、祖父结点有关，规律如下：
1. pNode为根节点或者pNode是其父结点的右孩子时，next结点为：

- **如果pNode有右子树**，那么next结点为右字树的最左叶节点
- **如果pNode没有右子树**，那么next结点分为3种情况:
    - **pNode的父结点为空或祖父结点为空**，next结点为空
    - **pNode的父节点是祖父结点的左孩子**，next结点为祖父结点
    - **pNode的父亲结点是祖父结点的右孩子**，那么next结点为空。

pNode为根的左结点时：
- 右子树为空，next结点为父结点
- 右子树非空，next结点为右子树的最左边结点
  接下来我们就可以开始写程序了。

/*
struct TreeLinkNode {
    int val;
    struct TreeLinkNode *left;
    struct TreeLinkNode *right;
    struct TreeLinkNode *next;
    TreeLinkNode(int x) :val(x), left(NULL), right(NULL), next(NULL) {

    }
};
*/
class Solution {
public:
    TreeLinkNode* GetNext(TreeLinkNode* pNode)
    {
        // 边界情况
        if(pNode == NULL) return NULL;

        if(pNode->next==NULL || pNode==pNode->next->right)
        {
            // pNode右子树为空
            if(pNode->right == NULL)
            {
                return GetNextHelper(pNode);
            }
            // pNode有右子树
            else
            {
                // 右子树的最左叶节点
                return GetLeftestLeaf(pNode->right);
            }
        }
        if(pNode == pNode->next->left)
        {
            // 右子树为空
            if(pNode->right == NULL)
                return pNode->next;
            //右子树非空
            else
                return GetLeftestLeaf(pNode->right);
        }

        //为了编译通过    
        return NULL;
    }
    TreeLinkNode* GetNextHelper(TreeLinkNode *pRoot)
    {
        // pNode父节点为空
        if(pRoot->next == NULL || pRoot->next->next==NULL) return NULL;

        // pNode父节点为组父节点的左孩子
        if(pRoot->next == pRoot->next->next->left)
            return pRoot->next->next;

        // pNode父节点为祖父节点的右孩子
        if(pRoot->next == pRoot->next->next->right)
        {    
            return NULL;
        }

        //为了编译通过    
        return NULL;
    }
    TreeLinkNode* GetLeftestLeaf(TreeLinkNode* pRoot)
    {
        TreeLinkNode *left = pRoot->left;
        if(left==NULL)
            return pRoot;
        else
            return GetLeftestLeaf(left);
    }
};

测试：

int main()
{
    TreeLinkNode* p8 = new TreeLinkNode(8);
    TreeLinkNode* p6 = new TreeLinkNode(6);
    TreeLinkNode* p10 = new TreeLinkNode(10);
    TreeLinkNode* p5 = new TreeLinkNode(5);
    TreeLinkNode* p7 = new TreeLinkNode(7);
    TreeLinkNode* p9 = new TreeLinkNode(9);
    TreeLinkNode* p11 = new TreeLinkNode(11);
    p8->left = p6;
    p8->right = p10;
    p6->left = p5;
    p6->right = p7;
    p6->next = p8;
    p10->left = p9;
    p10->right = p11;
    p10->next = p8;
    p5->next = p6;
    p7->next = p6;
    p9->next = p10;
    p11->next = p10;

    Solution s;
    TreeLinkNode* next = s.GetNext(p6);
    // cout<<next<<endl;
    if(next)
    {
        std::cout<<next->val<<std::endl;
    }
    return 0;
}

另一种思路：
上面我们从父节点与祖父结点的关系分类分析，还可以从有无右子树进行分析，ac代码如下，可以对比分析一下：

/*
struct TreeLinkNode {
    int val;
    struct TreeLinkNode *left;
    struct TreeLinkNode *right;
    struct TreeLinkNode *next;
    TreeLinkNode(int x) :val(x), left(NULL), right(NULL), next(NULL) {

    }
};
*/
class Solution {
public:
    TreeLinkNode* GetNext(TreeLinkNode* pNode)
    {
        if(pNode == NULL) return NULL;
        if(pNode->right == NULL)
            //

        {
            return GetF(pNode);
        }
        else