深度优先搜索(Depth-First-Search)

一：深度优先搜索(Depth-First-Search)

       从起点出发，走过的点要做标记，发现有没走过的点，就随意挑一个往前走，走不了就回退，此种路径搜索策略就称为“深度优先搜索”，简称“深搜”。
       其实称为“远度优先搜索”更容易理解些。因为这种策略能往前走一步就往前走一步，总是试图走得更远。所谓远近(或深度），就是以距离起点的步数来衡量的。

1：判断从V出发是否能走到终点：

bool Dfs(V) {  
    if( V 为终点） 
       return true; 
    if( V 为旧点) 
        return false; 
    将V标记为旧点; 
    对和V相邻的每个节点U { 
        if( Dfs(U) == true) 
            return true; 
    } 
    return false; 
} 
int main() { 
    将所有点都标记为新点; 
    起点 = 1 
    终点 = 8 
    cout << Dfs(起点）; 
} 

2：判断从V出发是否能走到终点,如果能，要记录路径：

Node path[MAX_LEN];  //MAX_LEN取节点总数即可 
int depth; 
bool Dfs(V) { 
    if( V为终点）{ 
       path[depth] = V; 
       return true; 
    } 
    if( V 为旧点) 
        return false; 
    将V标记为旧点; 
    path[depth]=V; 
    ++depth;
    对和V相邻的每个节点U { 
        if( Dfs(U) == true) 
            return true; 
    } 
    --depth; 
    return false;
} 
int main() { 
    将所有点都标记为新点; 
    depth = 0; 
    if( Dfs(起点）） { 
        for(int i = 0;i <= depth; ++ i) 
            cout << path[i] << endl; 
    } 
}

1->3->7->9=>7->A=>7=>3->5->6->8
path: 1,3,5,6,8

 

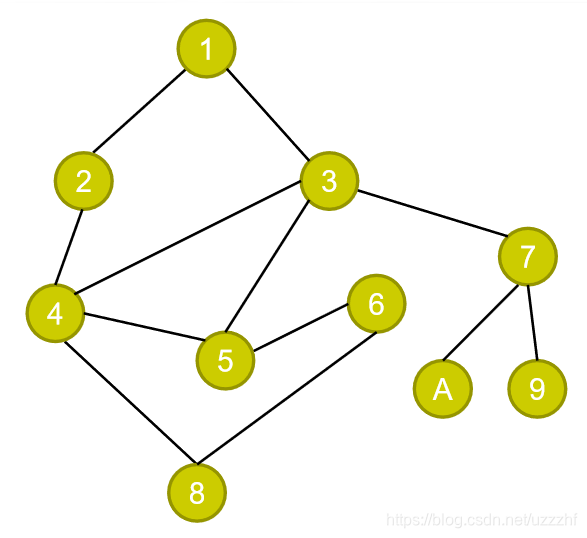
二：深度优先遍历图上所有节点

Dfs(V) { 
    if( V是旧点) 
        return; 
    将V标记为旧点; 
    对和V相邻的每个点 U { 
        Dfs(U); 
    }  
} 
int main() { 
    将所有点都标记为新点; 
    while(在图中能找到新点k) 
        Dfs(k); 
}