《【NOIP2018 普及组 基础】龙虎斗》 题解

目录

题目描述

输入描述

输出描述

解析

完整代码

---

描述

轩轩和凯凯正在玩一款叫《龙虎斗》的游戏，游戏的棋盘是一条线段，线段上有 n 个兵营（自左至右编号 1∼n），相邻编号的兵营之间相隔 1 厘米，即棋盘为长度为 n−1 厘米的线段。i 号兵营里有 ci​位工兵。 下面图 1 为 n=6 的示例：

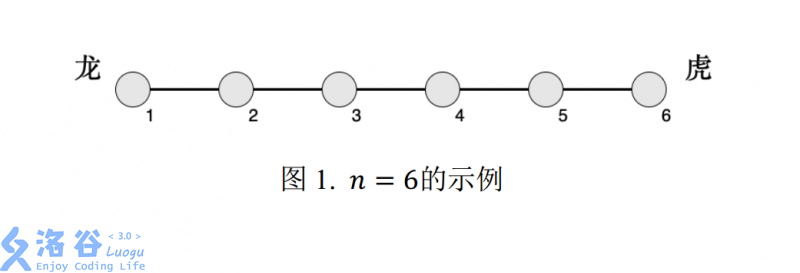
轩轩在左侧，代表“龙”；凯凯在右侧，代表“虎”。 他们以 m 号兵营作为分界， 靠左的工兵属于龙势力，靠右的工兵属于虎势力，而第 m 号兵营中的工兵很纠结，他们不属于任何一方。

一个兵营的气势为：该兵营中的工兵数× 该兵营到 m 号兵营的距离；参与游戏 一方的势力定义为：属于这一方所有兵营的气势之和。
下面图 2 为 n=6,m=4 的示例，其中红色为龙方，黄色为虎方：

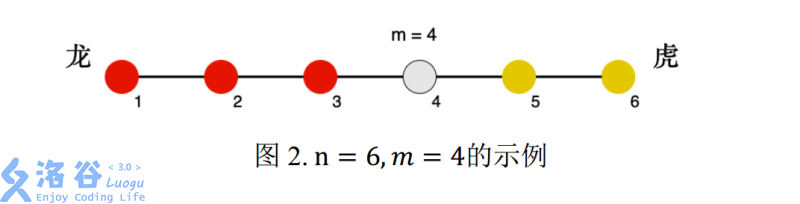
游戏过程中，某一刻天降神兵，共有 s1​ 位工兵突然出现在了 p1​ 号兵营。作为轩轩和凯凯的朋友，你知道如果龙虎双方气势差距太悬殊，轩轩和凯凯就不愿意继续玩下去了。为了让游戏继续，你需要选择一个兵营 p2​，并将你手里的 s2​ 位工兵全部派往 兵营 p2​，使得双方气势差距尽可能小。

注意：你手中的工兵落在哪个兵营，就和该兵营中其他工兵有相同的势力归属（如果落在 m 号兵营，则不属于任何势力）。

输入描述

输入文件的第一行包含一个正整数n，代表兵营的数量。

接下来的一行包含 n 个正整数，相邻两数之间以一个空格分隔，第 i 个正整数代 表编号为 i 的兵营中起始时的工兵数量 ci​。

接下来的一行包含四个正整数，相邻两数间以一个空格分隔，分别代表 m,p1​,s1​,s2​。

输出描述

输出文件有一行，包含一个正整数，即 p2​，表示你选择的兵营编号。如果存在多个编号同时满足最优，取最小的编号。

用例输入 1 

6
2 3 2 3 2 3
4 6 5 2

用例输出 1 

2

用例输入 2 

6 
1 1 1 1 1 16 
5 4 1 1

用例输出 2 

1

提示

【输入输出样例 1 说明】
见问题描述中的图 2。
双方以 m=4 号兵营分界，有 s1​=5 位工兵突然出现在 p1​=6 号兵营。
龙方的气势为：

2×(4−1)+3×(4−2)+2×(4−3)=14

虎方的气势为：

2×(5−4)+(3+5)×(6−4)=18

当你将手中的 s2​=2 位工兵派往 p2​=2 号兵营时，龙方的气势变为：

14+2×(4−2)=18

此时双方气势相等。

【输入输出样例 2 说明】

双方以 m=5 号兵营分界，有 s1​=1 位工兵突然出现在 p1​=4 号兵营。
龙方的气势为：

1×(5−1)+1×(5−2)+1×(5−3)+(1+1)×(5−4)=11

虎方的气势为：

16×(6−5)=16

当你将手中的 s2​=1 位工兵派往 p2​=1 号兵营时，龙方的气势变为：

11+1×(5−1)=15

此时可以使双方气势的差距最小。

【数据规模与约定】
1<m<n,1≤p1​≤n。
对于 20% 的数据，n=3,m=2,ci​=1,s1​,s2​≤100。
另有 20% 的数据，n≤10,p1​=m,ci​=1,s1​,s2​≤100。
对于 60% 的数据，n≤100,ci​=1,s1​,s2​≤100。
对于 80% 的数据，n≤100,ci​,s1​,s2​≤100。
对于 100% 的数据，n≤105,ci​,s1​,s2​≤109。

来源

noip复赛

兄弟们啊，不是你们c++学不会，而是个别老师他教不对啊。

来，就这题你看着懵不懵，懵不懵！

看看老高平时是怎么教我的：

要解决这个问题，我们需要实现以下步骤：

1. 读取输入数据，包括兵营数量 n、每个兵营的初始工兵数量 c、分界兵营 m、天降神兵的位置 p1 和数量 s1、以及你手中工兵的数量 s2。
2. 计算初始状态下龙方和虎方的气势。
3. 遍历所有可能的 p2 位置，计算在每个位置上放置 s2 工兵后的龙方和虎方的气势，记录使得双方气势差距最小的 p2 位置。
4. 输出使得气势差距最小的 p2 位置。

以下是实现这个逻辑的 C++ 代码（注意！下面代码不是正确的，正确代码在底下）：

 

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

int main() {
    int n;
    cin >> n;
    vector<ll> c(n + 1); // 兵营的工兵数量, c 不用, 从 c 到 c[n]
    for (int i = 1; i <= n; ++i) {
        cin >> c[i];
    }

    int m, p1, s1, s2;
    cin >> m >> p1 >> s1 >> s2;

    // 计算初始龙方和虎方的气势
    ll dragon_power = 0, tiger_power = 0;
    for (int i = 1; i < m; ++i) {
        dragon_power += c[i] * (m - i);
    }
    for (int i = m + 1; i <= n; ++i) {
        tiger_power += c[i] * (i - m);
    }

    // 天降神兵影响
    if (p1 < m) {
        dragon_power += s1 * (m - p1);
    } else if (p1 > m) {
        tiger_power += s1 * (p1 - m);
    }

    ll min_diff = abs(dragon_power - tiger_power);
    int best_p2 = 1;

    // 遍历所有可能的 p2，找到最优解
    for (int p2 = 1; p2 <= n; ++p2) {
        ll new_dragon_power = dragon_power;
        ll new_tiger_power = tiger_power;

        if (p2 < m) {
            new_dragon_power += s2 * (m - p2);
        } else if (p2 > m) {
            new_tiger_power += s2 * (p2 - m);
        }

        ll diff = abs(new_dragon_power - new_tiger_power);
        if (diff < min_diff || (diff == min_diff && p2 < best_p2)) {
            min_diff = diff;
            best_p2 = p2;
        }
    }

    cout << best_p2 << endl;
    return 0;
}

代码解释

1. ‌输入处理‌：

   • 读取兵营数量 n 和每个兵营的工兵数量 c。
   • 读取分界兵营 m、天降神兵的位置 p1 和数量 s1、以及你手中工兵的数量 s2。

2. ‌初始气势计算‌：

   • 遍历兵营，根据定义计算龙方和虎方的初始气势。

3. ‌天降神兵影响‌：

   • 根据 p1 的位置，更新龙方或虎方的气势。

4. ‌遍历寻找最优 p2‌：

   • 遍历所有可能的 p2 位置，计算放置 s2 工兵后的龙方和虎方的气势。
   • 记录使得双方气势差距最小的 p2 位置。如果有多个 p2 达到相同的最小差距，选择编号最小的 p2。

5. ‌输出结果‌：

   • 输出使得气势差距最小的 p2 位置。

这个实现考虑到了所有可能的 p2 位置，并保证了在找到最小差距的同时选择编号最小的 p2。时间复杂度为 O(n)，可以在题目给定的限制下高效运行。

接着，正确代码：

#include <bits/stdc++.h>
using namespace std;
int main(){
    long long n,c[1000001],qishi=0,m,p1,s1,s2,dragon=0,tiger=0,minx=0;
    cin>>n;
    for(long long i=1;i<=n;i++)cin>>c[i];
    cin>>m>>p1>>s1>>s2;
    c[p1]+=s1;
    for(int i=1;i<=n;i++){
        if(i<m)dragon+=c[i]*(m-i);
        if(i>m)tiger+=c[i]*(i-m);
    }
    minx=abs(tiger-dragon);
    qishi=m;
    for(int i=1;i<=n;i++){
        long long x=abs(dragon+s2*(m-i)-tiger);
        if(x<minx){
            minx=x;
            qishi=i;
        }
    }
    cout<<qishi;
    return 0;
}

结束了！

对了，忘说了一句话：

要想c++成绩好，就来jiabei小课堂。

还有，点我主页，看我简介，别给那三个人点赞就完了