《过河卒》 题解

目录

题目描述

输入描述

输出描述

解析

完整代码

---

题目描述

棋盘上 �A 点有一个过河卒，需要走到目标 �B 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 �C 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，�A 点 (0,0)(0,0)、�B 点 (�,�)(n,m)，同样马的位置坐标是需要给出的。

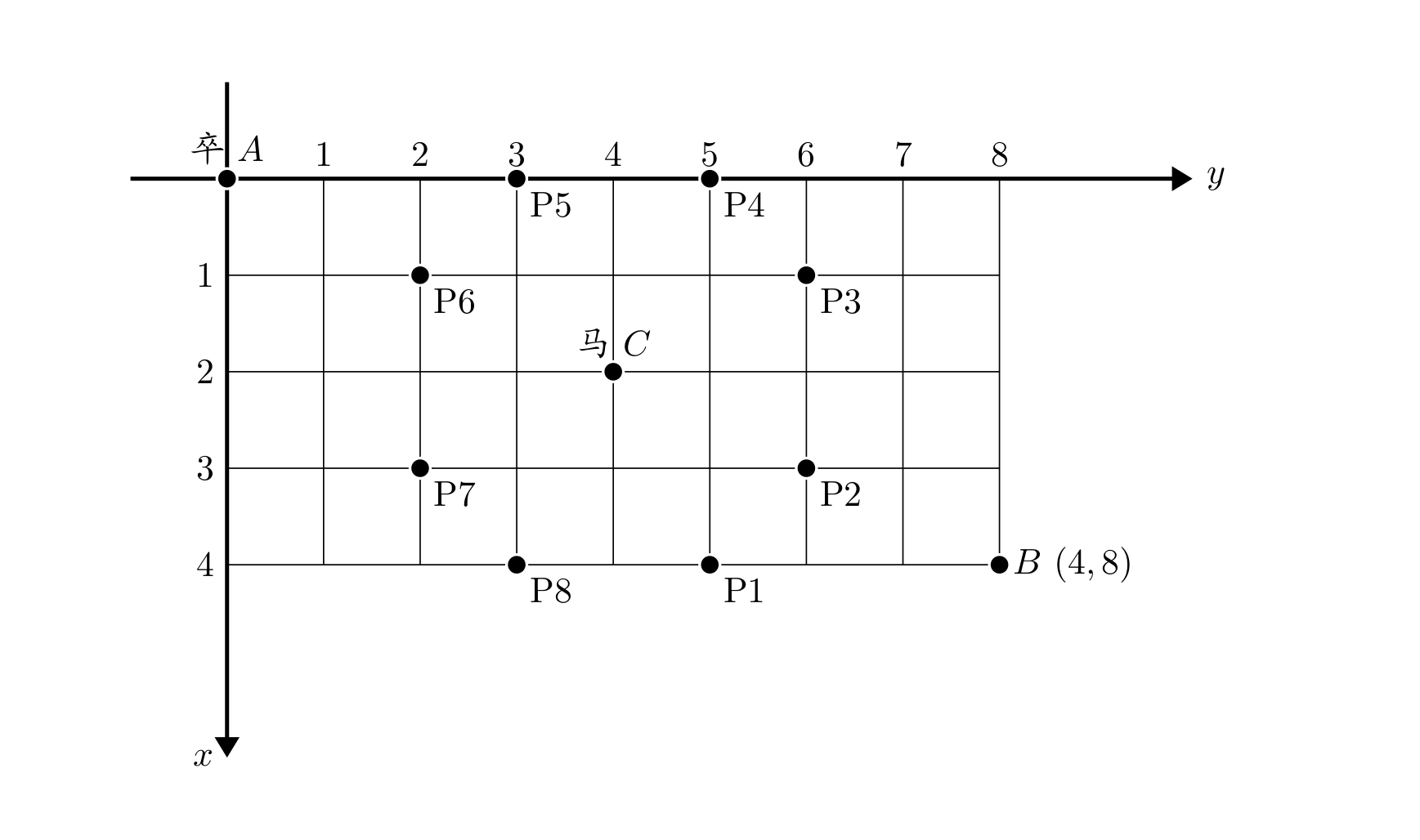
现在要求你计算出卒从 �A 点能够到达 �B 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 �B 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

输入输出样例

输入 #1复制

6 6 3 3

输出 #1复制

6

说明/提示

对于 100%100% 的数据，1≤�,�≤201≤n,m≤20，0≤0≤ 马的坐标 ≤20≤20。

【题目来源】

NOIP 2002 普及组第四题

一道比较入门的 dp 题

这道题初始位置是从 0 开始的，这样不是很利于我们解题，所以不如暂且把这题里涉及的坐标统统 +1，那么初始位置就从 (0,0)(0,0) 变成了 (1,1)(1,1)。

先考虑如果没有任何马的限制，卒子可以随便向右向下走，那么可以想到，一个卒子只能从 当前格子的左侧格子 和 当前格子的上方格子 上走到当前格子。那么假设从 (1,1)(1,1) 走到 当前格子的左侧格子 的路径条数是 �x，从 (1,1)(1,1) 走到 当前格子的上方格子 的路径条数是 �y，那么从 (1,1)(1,1) 走到当前格子的路径条数就应该是 �+�x+y。

其实我们已经得到了一个动态规划的转移方程，设 �(�,�)f(i,j) 表示从 (1,1)(1,1) 格子走到当前格子的路径条数，那么根据上一段得到的结论，可以得到：

�(�,�)=�(�−1,�)+�(�,�−1)f(i,j)=f(i−1,j)+f(i,j−1)

(�,�)(i,j) 是当前格子，那么 (�−1,�)(i−1,j) 就是 当前格子的上方格子，(�,�−1)(i,j−1)&