2023/5/28周报 Adam

摘要

This week, I learned some algorithms and strategies in machine learning, such as how to distinguish between Model bias and Optimization Issue, and deepened my understanding through some examples. In addition, it focuses on various situations of Optimization and corresponding treatment methods, such as how to deal with saddle points. Finally, various methods of adaptive learning rate are studied.

本周学习了机器学习中的一些算法和攻略，例如如何分辨是Model bias还是Optimization Issue，并通过一些例子来加深理解。此外，重点学习了Optimization的各种情形以及相对应的处理方法，例如遇到鞍点时应该如何处理。最后学习了自适应学习速率的各种方法。

机器学习任务攻略

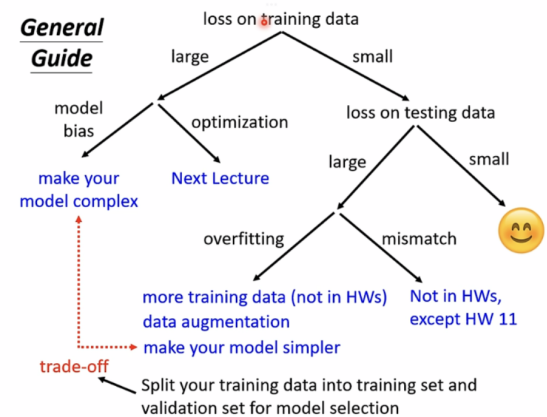
Model bias（模型偏差）
The model is too simple.
Solution：redesign the model to make it flexible

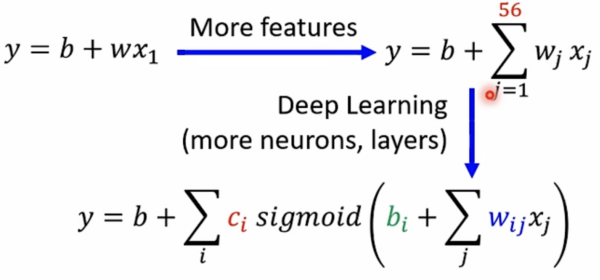
Optimization Issue（最优化出现问题）
梯度下降算法并未找出最优解

如何分辨是Model bias还是Optimization Issue？
Optimization Issue：

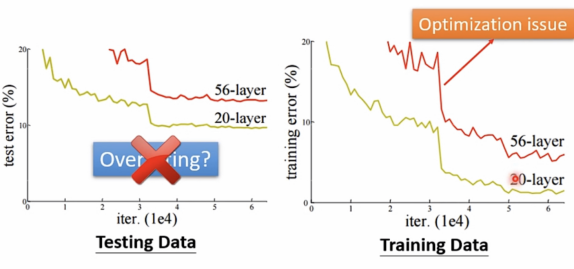
Gaining the insights from comparison
start from shallower network（or other models）which one is easier to optimize.
If deeper networks do not obtain smaller loss on training data,then there is optimization issue.
对比其他更简单的模型，如果更深层的网络不能在训练数据上获得更小的loss，说明出现了
optimization issue。

Solution: More powerful optimization technology 使用更有力的最优化方法
注： overfitting 是 small loss on training data,large loss on testing data.这里不是overfitting

for example：

这个例子里训练集很准，无误差，但实际上完全没有进行任何预测，毫无作用。

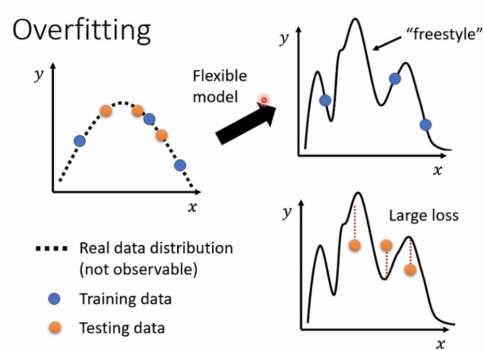
model太过于flexible，导致误差较大。
Solution： more training data（更多训练数据）
data augmentation（数据增强）
例如： 图像识别中对图片进行左右翻转，部分放大截图等等，但不可上下颠倒。
constrain model（限制模型）
例如： 限制function为一元二次。

How to constrain model？
Less parameters，sharing parameters（更少参数，共享参数）
Less features，early stopping，regularization，drop out
选择适当的model，不能太简单（model bias），也不能太过于复杂（overfitting）。

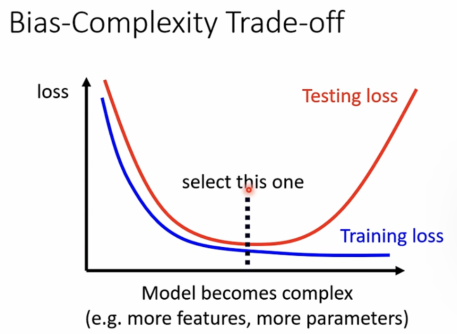
可以使用MSE（均方差）的方法计算比较，但并非完全可靠。

This explains why machine usually beats human on benchmark corpora.

Cross Validation（交叉验证）

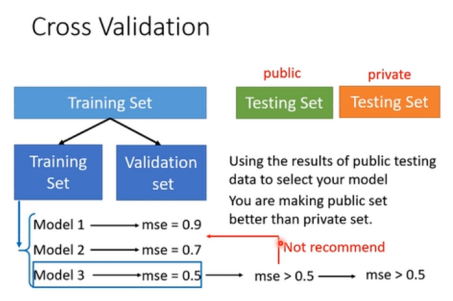
N-fold Cross Validation（N等分交叉验证）

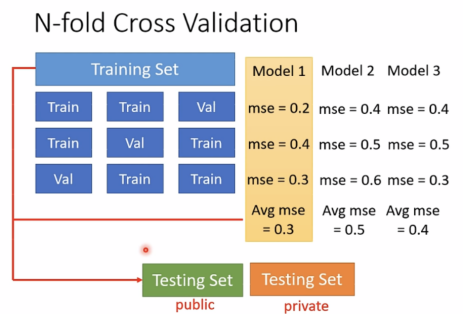
Mismatch
In fact training and testing data have different distributions
这种情况无法通过增加训练数据来解决。
Be aware of how data is generated.

局部最小值与鞍点

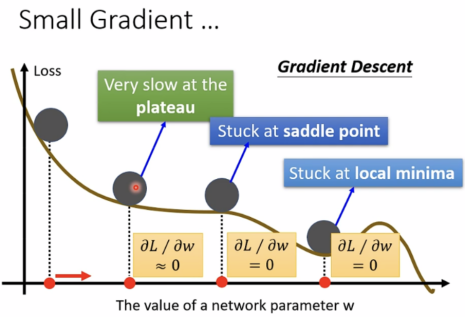
Situations when optimization fails.

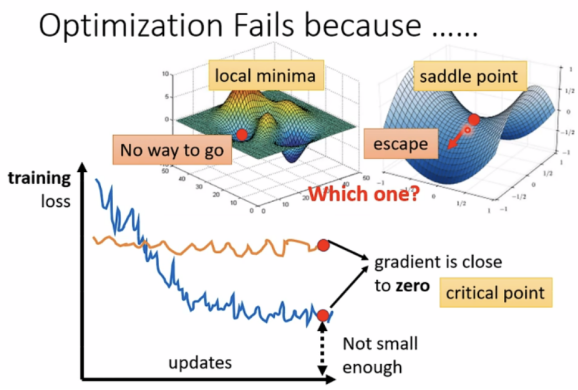
critical points（临界点）： 当gradient接近于0时
a.local minima：局部最小值（无路可走）
b.saddle points：鞍点（可逃离鞍点）

Tayler Series Approximation（泰勒级数近似）

Hessian（一种矩阵）
在critical point时，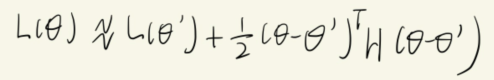
有以下情况：

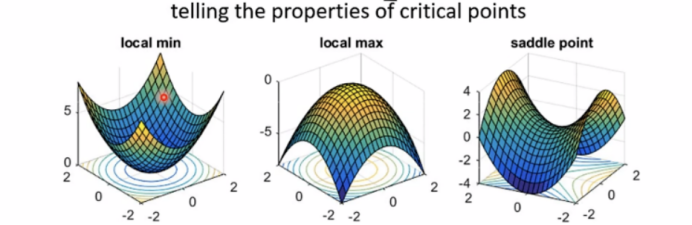
One example：



由以上可知，不必害怕saddle point。

遇到saddle point，H可以告诉我们更新前进的方向。
设u是H的一个特征向量，λ是u的特征值

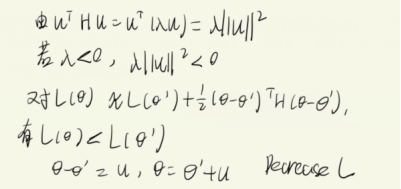
回到One example：
λ=-2时，特征向量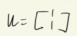，沿u的方向更新参数就可以找到更小的L。
此时可逃离saddle。

注：实际中，计算H的方法很少使用，因为计算较为复杂，可用其他方法代替。
eigenvalues 特征值 variance 误差，方差
eigen vector 特征向量 vanilla 一般的，普通的
error surface 误差曲面
从实验研究看，saddle point的情况要多于local minima

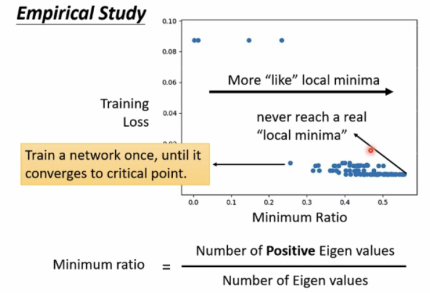
Batch and Momentum（批次与动量）

Batch
review：Optimization with Batch

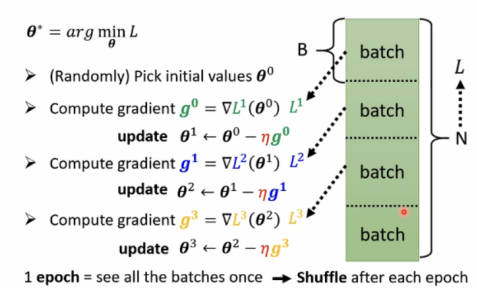
在每一次epoch后，还会重新分batch。

small batch与 large batch对比：
猜想：

然而事实上，通过GPU的平行计算的方式，更大的batch并不需要很长时间来计算gradient。

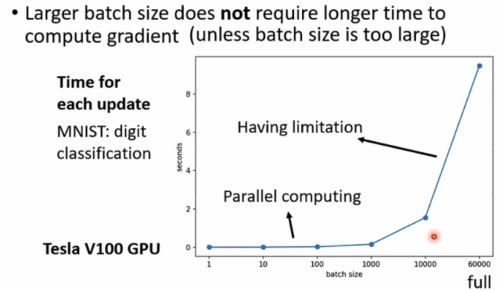
较小的batch反而需要更长时间来运行完一次epoch。

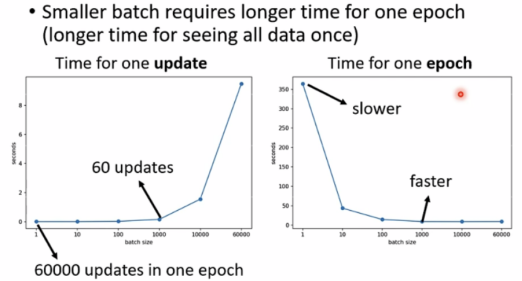
大的batch size is powerful，小的is noisy。但powerful不意味着准确率高，如下图较大batch size反而准确率低：

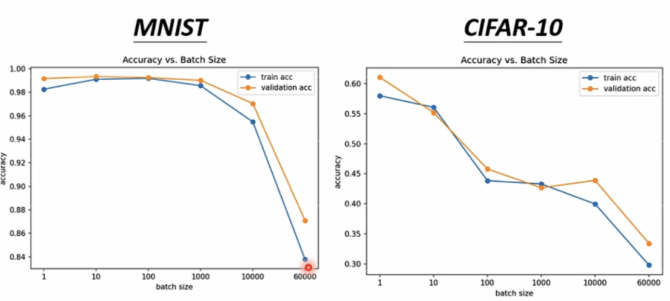
实际上noisy更新对training和testing更好：

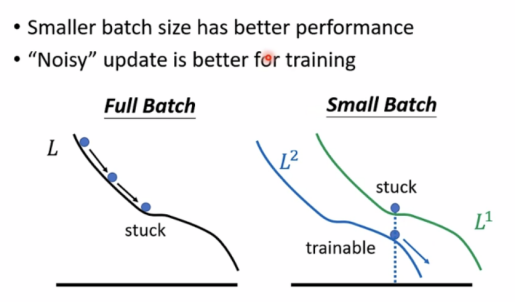
small batch size performs better on training and testing.

大小batch总结:

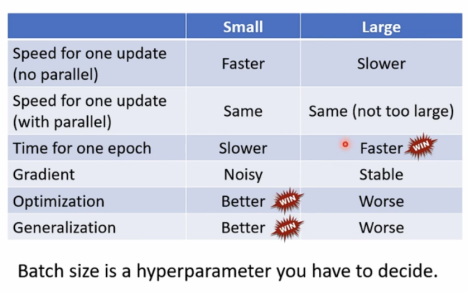
batch size也是可调节的hyperparameter

momentum
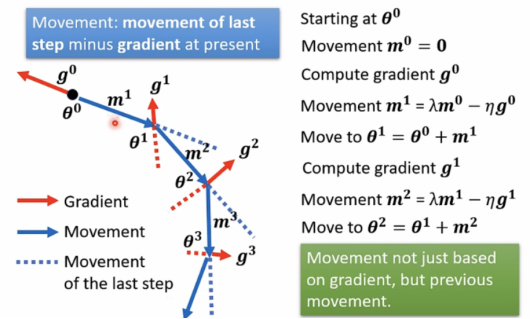
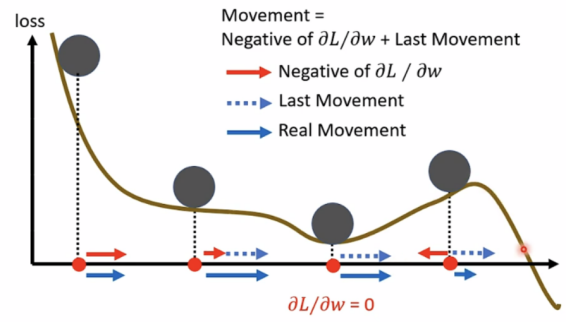
用Gradient+Momentum的方式，则movement方向改变，不再只往gradient反方向移动参数，新方向是反方向加上前一步调整的结果。

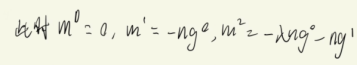
Concluding Remarks

Adaptive Learing Rate（自适应学习速率）

Training stuck≠small gradient

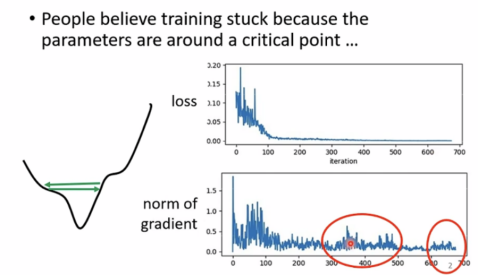
事实上，Training即使不遇到critical point也是十分困难的一件事。

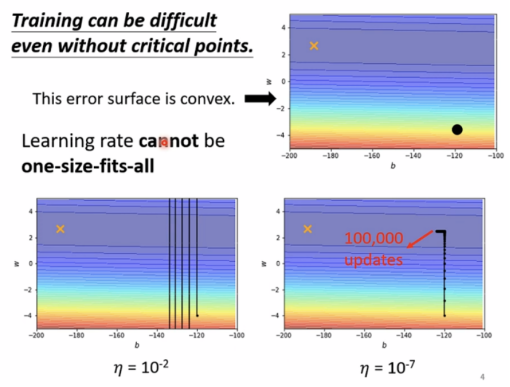
Different parameters needs different learning rate
陡峭时需要较小的学习速率，平缓时需要较大的学习速率。
可以先考虑只有一个parameter的情形：

Root Mean Square（均方差）

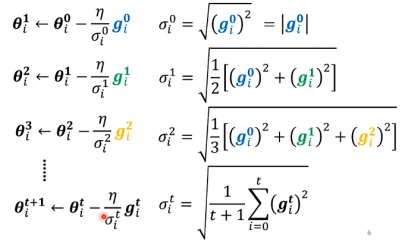
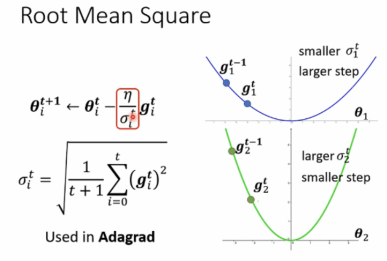
这种方法使用于Adagrad（自适应梯度算法）。

RMSProp（解决Adagrad方法学习速度衰减的问题）

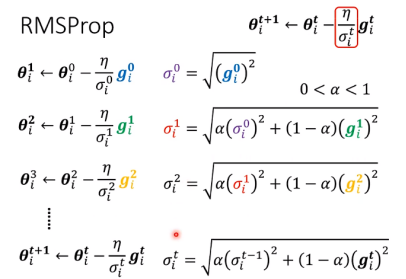
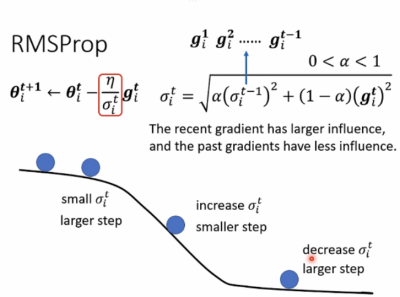
此外还有种Adam方法：RMSProp+Momentum

Adagrad缺点如下：

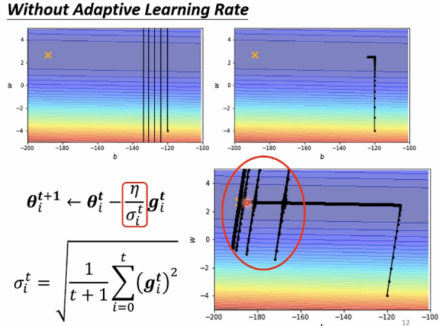
Solution：
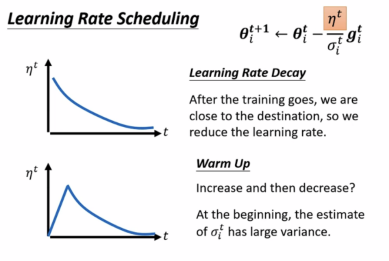
使用Learing Rate Scheduling

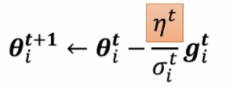
让学习率与时间有关，如learning rate delay（随着时间增加学习率减少），warm up（随时间增加，学习率先增加后减少）:


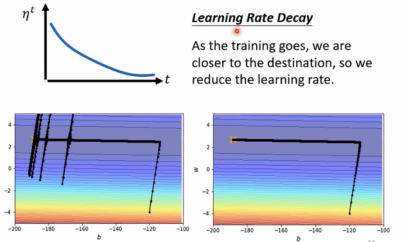
summary of optimization：


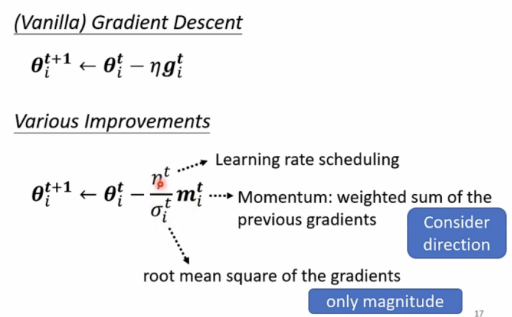
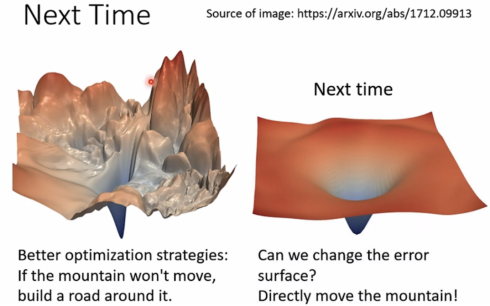
目前都是绕过崎岖的点，接下来还有些方法可以直接移平整座山。
注：magnitude 数值大小 variance 误差，方差
vanilla 一般的，普通的
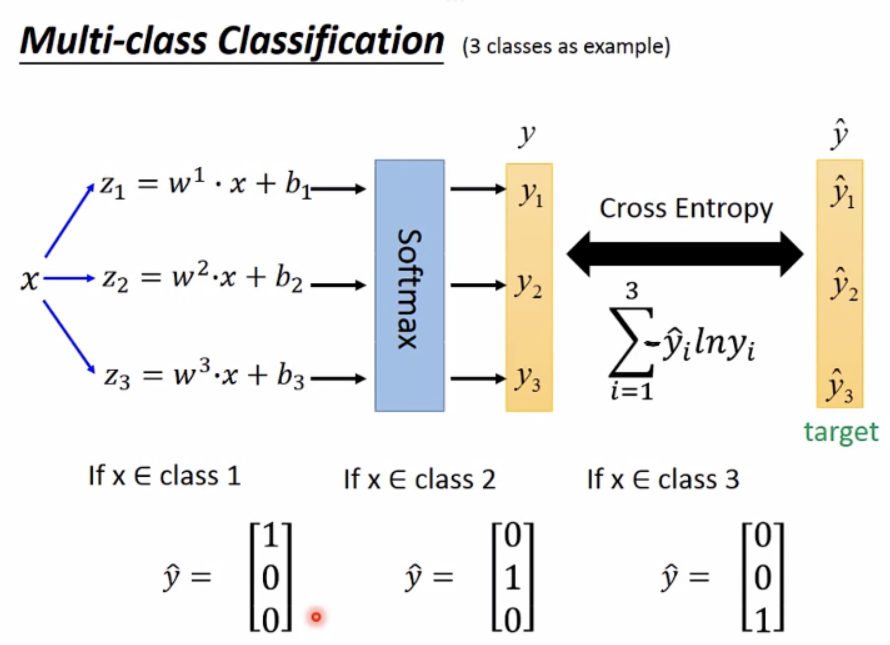
注： softmax

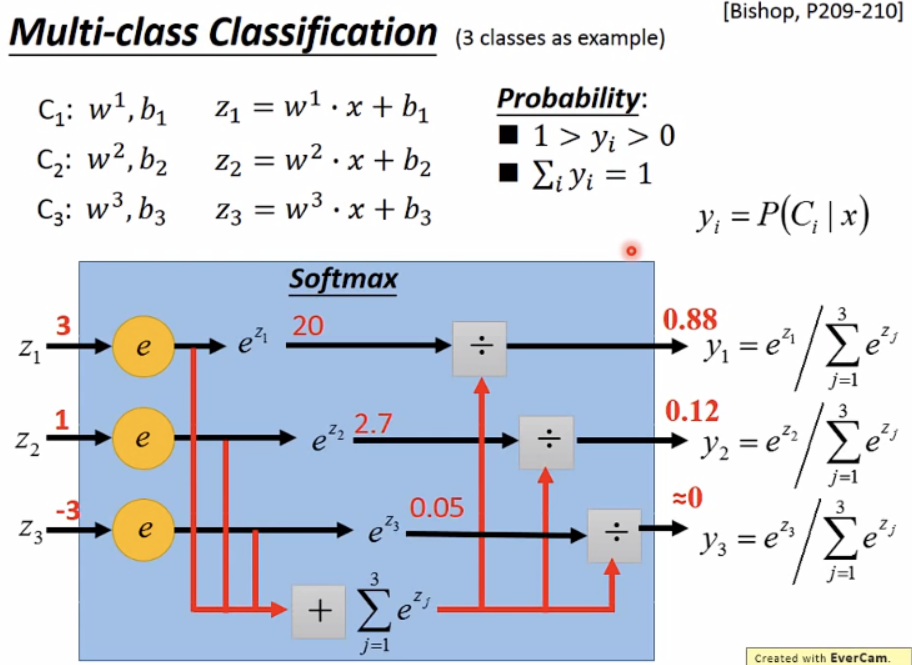
总结

本周研究了机器学习中遇到问题应该如何解决，例如如何绕过鞍点等等。下周将继续学习新的解决方法以及CNN卷积神经网络。