深入理解 javascript 排序算法

对于前端开发一般在实际应用中算法用得不算多， 不过一向对于面试造航母，工作拎螺丝。考察算法也是现在大公司必考的题，排序更是经常命中的题。

排序时间复杂度和空间复杂度对比：

以下列出常用的排序方式，性能（差 => 优）

公共代码调换数组两个下标的位置

const swap = function (array, index1, index2) {
    [array[index1], array[index2]] = [array[index2], array[index1]];
}

冒泡排序

冒泡排序比较任何两个相邻的项，如果第一个比第二个大，则交换它们。元素项向上移动至 正确的顺序，就好像气泡升至表面一样，冒泡排序因此得名。

bubbleSort(array) {
  let length = this.array.length;
  for (let i = 0; i < length; i++) {
    for (let j = 0; j < length - 1; j++) {
      if (array[j] > array[j + 1]) {
        swap(array, j, j + 1)
      }
    }
  }
  return array
}

• 图示
  
• 优化后冒泡排序

跳过已经排序过的循环，在正确位置上的数字没有被比较。即便我们做了这个小改变，改进
了一下冒泡排序算法，但我们还是不推荐该算法，它的复杂度是O(n2)。

const modifiedBubbleSort = function (array) {
  let length = array.length;
  for (let i = 0; i<length; i++) {
    for (let j = 0; j<length-1-i; j++) {
      if (array[j]> array[j+1]) {
          swap(array, j, j+1)
      }
    }
  }
  return array
}

图示：

选择排序

选择排序算法是一种原址比较排序算法。选择排序大致的思路是找到数据结构中的最小值并
将其放置在第一位，接着找到第二小的值并将其放在第二位

selectionSort(array) {
  let length = array.length,
      indexMin;

  for (let i = 0; i < length; i++) {
    indexMin = i;
    for (let j = i; j < length; j++) {
      if (array[indexMin] > array[j]) {
        indexMin = j;
      }
    }
    if (i !== indexMin) {
      swap(array, i, indexMin);
    }
  }
  return array
}

图示：

插入排序

插入排序每次排一个数组项，以此方式构建最后的排序数组。假定第一项已经排序了，接着， 它和第二项进行比较，第二项是应该待在原位还是插到第一项之前呢?这样，头两项就已正确排 序，接着和第三项比较(它是该插入到第一、第二还是第三的位置呢?)

	insertionSort(array) {
	        let length = array.length,
	            j, temp;
	        for (let i = 1; i < length; i++) {
	            j = i;
	            temp =array[i];
	            while (j > 0 && array[j - 1] > temp) {
	                array[j] = array[j - 1];
	                j--
	            }
	            array[j] = temp;
	        }
	        return array
	}

图示：

归并排序

归并排序是一种分治算法。其思想是将原始数组切分成较小的数组，直到每个小数组只有一 个位置，接着将小数组归并成较大的数组，直到最后只有一个排序完毕的大数组.

// 将拆好的小数组合并成一个大数组
const merge = function (left, right) {
    var result = [],
        il = 0,
        ir = 0;

    while (il < left.length && ir < right.length) {
        if (left[il] < right[ir]) {
            result.push(left[il++])
        } else {
            result.push(right[ir++])
        }
    }

    while (il < left.length) {
        result.push(left[il++])
    }

    while (ir < right.length) {
        result.push(right[ir++])
    }

    return result;
}
//将大数组递归拆成小数组
const mergeSortRec = function (array) {
    let length = array.length;

    if (length === 1) {
        return array;
    }

    let mid = Math.floor(length / 2),
        left = array.slice(0, mid),
        right = array.slice(mid, length);

    return merge(mergeSortRec(left), mergeSortRec(right))
}

执行图示：

通过在merge函数debug 查看left和right的值同样也可以看到每次传进来left和right的变化。

快排

快速排序也许是最常用的排序算法了。它的复杂度为O(nlogn)，且它的性能通常比其他的复 杂度为O(nlogn)的排序算法要好。和归并排序一样，快速排序也使用分治的方法，将原始数组分 为较小的数组

const partition = function (array, left, right) {
    let pivot = array[Math.floor((right + left) / 2)], // 选择主元
        i = left, // 初始化数组的第一个元素
        j = right; // 初始化数组的最后一个元素

    while (i <= j) { // 只要left和right没有相互交错就执行划分
        while (array[i] < pivot) {// 移动left指针直到找到一个元素比主元大
            i++
        }
        
        while (array[j] > pivot) { // 移动right指针直到找到一个元素比主元小
            j--;
        }
        
        if (i <= j) { // 如果左项大于左项则交换， 然后移动两个指针并重复此过程
            swap(array, i, j);
            i++;
            j--
        }
    }
    return i;
}

// 快排
const quick = function (array, left, right) {
    let index;

    if (array.length > 1) {
        index = partition(array, left, right)
        if (left < index - 1) {
            quick(array, left, index - 1)
        }

        if (index < right) {
            quick(array, index, right)
        }
    }
}

cosnt array = [3, 5, 1, 6, 4, 7, 2];
quick(array, 0, array.length - 1)

partition 执行示意图

第一次执行化分，得出i在索引为5的位置 ，所以quick第一次Index = 5，往下执行
quick(array, left, index - 1)此时7和6 排出不进行化分。

此时Index的值为1, right最大值为4
执行进入if (index < right) { quick(array, index, right) }此时对[5,3,2,4]再做划分

此时Index值为2 再次进入递归对[2, 3]进行划分， left指向2， right指向3 开始。

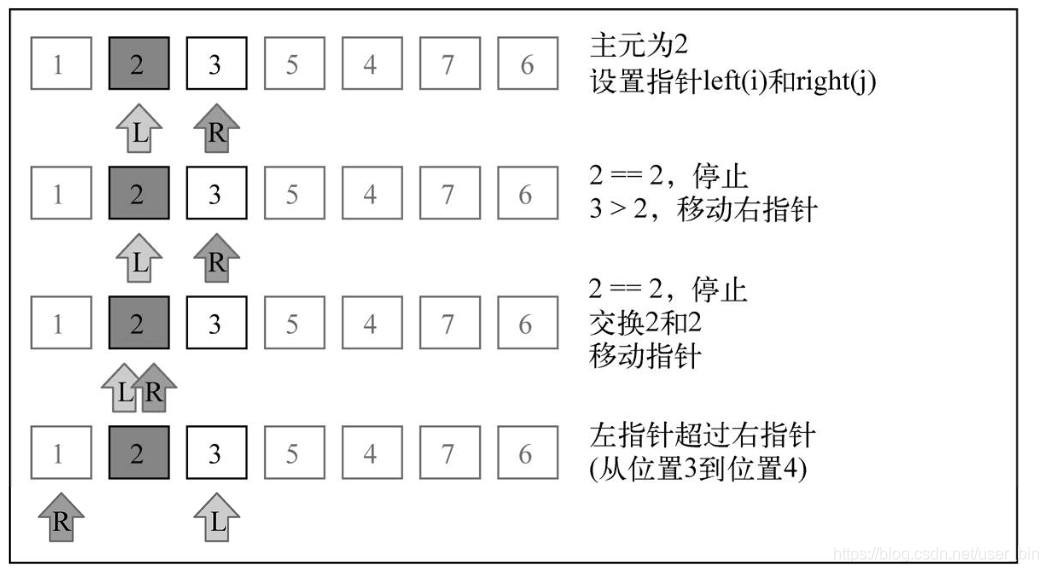
然后对[5, 4]进行划分排序和6，7进行划分排序

堆排

堆排序也是一种很高效的算法，因其把数组当作二叉树来排序而得名

数组转为二叉树规则：

• 索引0是树的根节点
• 除根节点外，任意节点N的父节点是N/2。
• 节点L的左子节点是 2 * L
• 节点R的右子节点是2*R+1

举例：
如数组 arr = [3, 5, 1, 6, 4, 7, 2]根据以上规则转换：
根节点为3,index = 0，则左子节点为 index * 2 + 1右子节点index * 2 + 2,所以3左子节点为arr[index * 2 + 1]，右子节点为arr[index * 2 + 2]对应如下图:

// 生成大顶堆
const buildHeap = function (array) {
    const heapSize = array.length;
    for (var i = Math.floor(array.length / 2); i >= 0; i--) {
        heapify(array, heapSize, i);
    }
}

// 对比交换位置
var heapify = function (array, heapSize, i) {
    let left = i * 2 + 1, // 左子节点
        right = i * 2 + 2, // 右子节点
        largest = i; // 父节点

    // 是否左子节点的值比当前节点值更大
    if (left < heapSize && array[left] > array[largest]) {
        largest = left;
    }

    // 是否右子节点的值比当前节点值大
    if (right < heapSize && array[right] > array[largest]) {
        largest = right;
    }

    // 如果当前父节点值不是最大的，
    if (largest !== i) {
        // 调整堆的位置
        swap(array, i, largest);
        // 然后再对当前的树进行比对
        heapify(array, heapSize, largest)
    }
}
const heapSort = function (array) {
	let heapSize = array.length;
    // 生成 大顶堆
    buildHeap(array);
    // 此时大顶堆顶部值是最大的， 即为数组的索引0
    while (heapSize > 1) {
        heapSize--;
        swap(array, 0, heapSize);
        heapify(array, heapSize, 0)
    }
	return array
}

文章主要摘要：[1] javascript数据结构与算法，
[2] https://www.geeksforgeeks.org/analysis-of-different-sorting-techniques/