平衡二叉树-python_python 题目一:平衡二叉树-优快云博客

本文链接：https://blog.youkuaiyun.com/unseven/article/details/123022810

该篇博客探讨了LeetCode第110题——平衡二叉树的判断问题。通过递归方法实现，当遇到空节点时返回0，计算左右子树深度，如果左右子树深度差超过1则返回-1，否则返回最大深度加1。示例展示了不同情况的输入及对应的输出。递归函数在平衡二叉树的判断中起到了关键作用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

leetCode第110题平衡二叉树
链接：https://leetcode-cn.com/problems/balanced-binary-tree

给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：
一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。

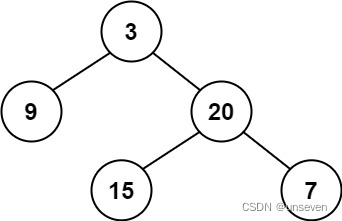
示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：true

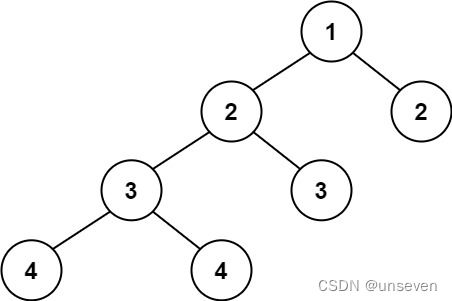
示例 2：

输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

提示：

树中的节点数在范围 [0, 5000] 内
-104 <= Node.val <= 104

平衡二叉树的定义就是每一个结点的左右子树的高度差不能超过1.
如果子树不是平衡二叉树那么这棵树就一定不会是平衡二叉树，那么完全可以通过递归来解决。
定义递归函数，root为None时，说明到了树的最底层的更下面，返回深度为0.
否则继续统计左子树和右子树的深度。
当左右高度差超过1时，那么返回-1，证明树绝不可能时平衡二叉树；当左边深度是-1或者右边深度是-1时，直接返回-1。
否则选出左右高度最大的一边，将高度+1再返回

## python3
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        if root == None:
            return True
        return self.helper(root) != -1
    def helper(self,root: TreeNode) -> int :
        if root == None:
            return 0
        left = self.helper(root.left)
        right = self.helper(root.right)
        if left == -1 or right == -1 or abs(left - right) > 1:
            return -1
        return max(left,right)+1