POJ 2411 Mondriaan's Dream（状压 dp）

最新推荐文章于 2021-07-29 15:52:01 发布

原创最新推荐文章于 2021-07-29 15:52:01 发布 · 494 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#状压dp

DP 动态规划专栏收录该内容

142 篇文章

订阅专栏

本文介绍了一个算法问题，即使用尺寸为2×1的小矩形来填充一个较大的矩形的方法数量计算。该问题源自荷兰画家皮特·蒙德里安的一个梦境，并通过动态规划方法解决，实现了对不同大小的大矩形的有效填充计数。

Language:

Mondriaan's Dream

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 12403		Accepted: 7237

Description

Squares and rectangles fascinated the famous Dutch painter Piet Mondriaan. One night, after producing the drawings in his 'toilet series' (where he had to use his toilet paper to draw on, for all of his paper was filled with squares and rectangles), he dreamt of filling a large rectangle with small rectangles of width 2 and height 1 in varying ways.

Expert as he was in this material, he saw at a glance that he'll need a computer to calculate the number of ways to fill the large rectangle whose dimensions were integer values, as well. Help him, so that his dream won't turn into a nightmare!

Input

The input contains several test cases. Each test case is made up of two integer numbers: the height h and the width w of the large rectangle. Input is terminated by h=w=0. Otherwise, 1<=h,w<=11.

Output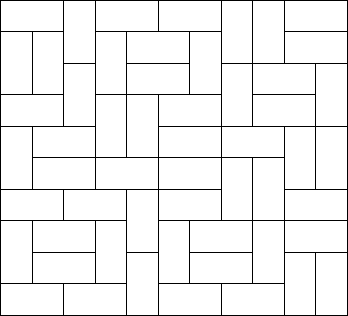

For each test case, output the number of different ways the given rectangle can be filled with small rectangles of size 2 times 1. Assume the given large rectangle is oriented, i.e. count symmetrical tilings multiple times.

Sample Input

Sample Output

Source

Ulm Local 2000

有砖铺满为1，无砖为0，看成下一行可以像上一行差砖的模式进行枚举哪么状态可以转移

这里第一行需要单独处理，哪么每个1应该是连续的2个

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>
#include<set>
#include<map>


#define L(x) (x<<1)
#define R(x) (x<<1|1)
#define MID(x,y) ((x+y)>>1)

#define eps 1e-8
typedef __int64 ll;

#define fre(i,a,b)  for(i = a; i <b; i++)
#define mem(t, v)   memset ((t) , v, sizeof(t))
#define sf(n)       scanf("%d", &n)
#define sff(a,b)    scanf("%d %d", &a, &b)
#define sfff(a,b,c) scanf("%d %d %d", &a, &b, &c)
#define pf          printf
#define bug         pf("Hi\n")

using namespace std;

#define INF 0x3f3f3f3f
#define N 10005

ll dp[12][1<<12];

int n,m;

bool ok(int x)
{
    int i;
    for(i=0;i<m;)
	{
		if((1<<i)&x)
		{
			if(i==m-1) return false;
			if((1<<(i+1))&x) i+=2;
			else return false;
		}
		else
			i++;
	}
	return true;
}

bool okk(int down,int up)
{
	int i;
	for(i=0;i<m;)
	{                             //列
		  if((1<<i)&down)        //(i)=1
		  {
		  	 if(up&(1<<i))       //（i-1）==1
			 {
			 	 if(i==m-1||!(up&(1<<(i+1)))||!(down&(1<<(i+1))))    //那么这个砖是横放的 上一行的i+1应该为1
					return false;                                    //                    这一行的i+1应该为1
				 i+=2;
			 }
			 else
			    i++;   这一块砖插入上一行
		  }
		  else
		  {
		  	  if(up&(1<<i)) i++;    //这一行i=0,那么上一行一定要为1
		  	  else return false;
		  }
	}
	return true;
}

int main()
{
	int i,j;
	while(sff(n,m),n+m)
	{
		if(n<m) swap(n,m);

		if(n%2&&m%2)
		{
			pf("0\n");
			continue;
		}

		mem(dp,0);
        int len=1<<m;

	    fre(i,0,len)
		   if(ok(i))
			dp[0][i]=1;

		int up,down;


		fre(i,1,n)
		{
			fre(down,0,len)
			  fre(up,0,len)
			   if(okk(down,up))
				 dp[i][down]+=dp[i-1][up];
		}

		pf("%I64d\n",dp[n-1][len-1]);

	}
	return 0;
}