全波形反演之卷积、自相关、互相关（2）

最新推荐文章于 2025-04-20 23:06:56 发布

苗妮

最新推荐文章于 2025-04-20 23:06:56 发布

阅读量673

点赞数

分类专栏：地震勘探原理文章标签：人工智能

本文链接：https://blog.youkuaiyun.com/u014655960/article/details/134967382

版权

地震勘探原理专栏收录该内容

8 篇文章

订阅专栏

使用深度学习的全波形反演方案，面临的一个重要问题就是带标签的数据不足，往往我们会从合成尽可能真实的速度模型（输出标签）和地震数据（输入数据）入手。

通常的做法，当获得足够多的合成数据时，在合成数据上训练，在真实数据上测试。

然而，合成数据往往无法捕捉现场/真实实验的真实性，导致训练好的神经网络在推理阶段性能较差。

有学者，从信号处理的角度，利用卷积、自相关、互相关等，描述了一类新的方法来增强对具有真实数据特征的合成数据的监督训练（领域自适应）。

1、方案一（卷积减轻波形源效应）：

Choi Y, Alkhalifah T. Source-independent time-domain waveform inversion using convolved wavefields: Application to the encoded multisource waveform inversion[J]. Geophysics, 2011, 76(5): R125-R134.

1）算法描述

动机：传统的全波形反演需要对源小波进行良好的估计，论文开发了使用卷积波场的与源无关的时域波形反演。

方法：在损失函数的计算中，观测波场与来自建模波场的参考迹线卷积，再加上建模波场与观测波场的基准迹线的卷积。

贡献：

1) 损失函数中，对观测和建模波场的源小波进行卷积，并且从而消除了两波场源小波差异对反演结果的影响。

2）建模的波场起到低通滤波的作用，观测到的波场在失配函数中，只需设置建模波场的源小波的最大频率，就可以很容易地采用从低到高的频率选择策略；因此不需要滤波。（不是很理解）

3）损失函数的梯度计算方法。（传统全波形反演关注、深度方法不考虑）

经验与局限性：

当将随机噪声添加到合成数据中时，方法存在局限性。与使用单道数据相比，多道数据的平均值是参考迹线的更好选择。

2）理论分析

下述一、二式等价。其中，E表述损失函数。u表示建模（合成）数据，d表示观测（真实）数据。

ns表示炮数、nr表示道数。g表示格林函数、s表示子波。

下述三、四式等价。通过对上述一式，观测波场与来自建模波场的参考迹线卷积、建模波场与观测波场的基准迹线的卷积，再结合卷积运算的线性性质，目前的子波变成了 $S^{u} \ast S^{d}$ ，消除了不同子波对全波形反演的影响，求解目标为g格林函数。

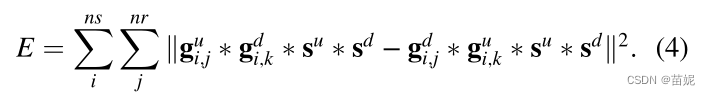
我的思考： 这四个g之间其实也有误差，那这4个g之间的关系是怎样的？

3）卷积的作用

将观测数据与合成数据进行卷积的过程，以反演速度模型，有助于减少波形源效应对目标函数的影响。

2、方案二（相关操作实现压缩数据、滤除随机噪声的作用）：

Wang H, Alkhalifah T. Direct microseismic event location and characterization from passive seismic data using convolutional neural networks[J]. Geophysics, 2021, 86(6): KS109-KS121.

1）相关操作压缩数据

将数据与参考迹线相关操作后，可以有效减少数据量，如下图所示。并且有效减少训练和测试数据分布的方差（方案三对此论文的评述）。

2）相关操作滤除噪声

依据维纳-辛勤定理，噪声每一时刻都不同，自相关后噪声就趋近于0了，也实现了去噪功能，相当于低通滤波器。

3、方案三（涉及卷积、自相关、互相关）：

Alkhalifah T, Wang H, Ovcharenko O. MLReal: Bridging the gap between training on synthetic data and real data applications in machine learning[C]//82nd EAGE Annual Conference & Exhibition. European Association of Geoscientists & Engineers, 2021, 2021(1): 1-5.

本方案的基本动机同方案一一致，在地震震源定位和低频外推两个任务中，取得较好的效果。

并且明确，此种数据增强手段对于输入数据的纵轴（时间或深度）的绝对值不是关键的任务都非常有效。