约会推荐系统-优快云博客

本文链接：https://blog.youkuaiyun.com/u014296502/article/details/80213687

都说女人是善变的，做的每个决定都让我们男性同胞找不到任何根据，于是就有了女人的心思你别猜。但是很多时候我们需要知道她们在想什么，知己知彼才能百战不殆，少一点争吵，少一些矛盾，少一些猜疑。于是这个维护世界和平，共同创造和谐社会的责任就让我来承担一些吧！相信很多男同胞都会遇到这个问题：约女孩出来吃饭；这个问题看似简单，其实不然，吃饭要吃出水平，而且要结合女孩的心思，否则很容易让女孩觉得你不解风情，根本不了解她，或者你的女朋友自己也没什么想法，就想让你出个好点子，取吃些想吃的东西。一般的人会使用穷举法，列出附近所有好吃的，让女孩挑选，个人觉得如果每次都这样，很容易让人产生一种不愉快感。看似女孩的心思与决定都是随机的我们无法预测，但是我相信哲学里面的一句话“联系是普遍存在的“，也就是说女孩所作出的决定肯定有规律可循，这次就让我们使用统计机器学习最大熵模型的手段，来解决每次约女孩吃饭的问题。假如我们约到女孩了，我们如何去决定一个最符合女孩想吃食物的类型，比如说：小吃、火锅、自助餐、地锅鸡、鸡公煲、鸭血粉丝、韩式料理等。首先我们要对女孩心思的不确定进行一种度量，熵就是对随机变量不确定性的度量，可以借助熵来量化这种不确定性。假设P(‘吃饭’)模型是估计的概率分布，它是对确定性的一种度量。假设P(‘吃饭’=‘火锅’)=90%，也就是说这个女孩喜欢吃火锅，我很确定下次约她，如果我要求吃火锅她会很开心。因为我很确定。为什么呢？我们对概率取log并加个负值，得 $i(x=‘火锅’)=-log(p('吃饭'=‘火锅’))$ 是一个很小的值，其中 $i(x)$ 函数被称为自信息，是对不确定性的一种度量，既然吃火锅的不确定性很低，那么是不是就说明应该去吃火锅呢？嘿嘿！！对自信息取期望，就得到了的熵的定义：

H (x) = - \sum P (x) l o g P (x)

$H(x)=-\sum P(x)logP(x)$
如何得到“吃饭”模型的概率分布呢？一般想吃什么，是由心情决定的，我们能从什么角度知道，女孩的心情呢？对穿衣打扮，穿衣打扮大概能够得出这个女孩的当前心情状态，这其实就是特征提取的过程。
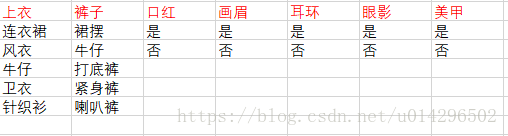
这里写图片描述

定义好特征之后，就是数据采集的过程，你需要先去成功的约出女孩，然后询问她想吃什么（标签），然后注意的她的穿衣打扮，做好数据录入。因为样本采集成本非常高，所以我采集了4个样本。

这里写图片描述

有了样本，我希望下次我看到下次约她出来看到她的穿衣，我能够提供更好建议（针对不同的女孩你需要做成更多的努力采集样本，针对女孩的不同模型不具有唯一性），这里引出互信息的定义：

i (x, y) = i (y) - i (y | x) = l o g (p (y | x) / p (x))

$i(x,y)=i(y)-i(y|x)=log(p(y|x)/p(x))$
互信息衡量了，特征与标签之间的相关性，同理取互信息的均值：

I (x, y) = \sum x, y p (x, y) l o g p ( x , y ) p ( x ) p ( y )

$I(x,y)=\sum_{x,y}p(x,y)log \frac{p(x,y)}{p(x)p(y)}$ 是不是有似曾相识的感觉？对，这就是决策树中“信息增益”的定义，ID3算法中，是如果信息增益大则对这个特征划分，使得节点尽可能的“纯净”。有了上面的定义，也就是说模型可以通过学习“穿衣打扮”特征，得到一个决策模型。
最大熵模型的原理：最大熵原理是概率模型学习中的一个准则，最大熵原理认为，学习概率模型时候，在所有可能的概率模型中，熵最大的模型是最好的模型。最大熵原理认为在满足已有事实，即约束条件，那些不确定的部分都是“等可能的”，最大熵原理通过熵的最大化表示等可能。具体啥意思呢？就是假设你对象是清真女孩，那就是不吃猪肉之类的，除去她不吃的（满足约束），最大熵模型认为，她爱吃牛肉、羊肉的概率是相等的。

p(′羊肉′)=p(′牛肉′)p(′羊肉′)=p(′牛肉′) $p('羊肉')=p('牛肉')$ ，或者她更爱吃素，偶然会吃肉，那么就可以认为

p(′素食′)>0.5p(′素食′)>0.5 $p('素食')>0.5$ 假设

p(′素食′)=0.6p(′素食′)=0.6 $p('素食')=0.6$ 那么在满足这个约束条件的时候，你并不知道她更爱吃牛肉还是羊肉，那么在这个不确定的情况下，为了保持熵的最大化，我们可以认为

p(′羊肉′)=p(′牛肉′)=0.2p(′羊肉′)=p(′牛肉′)=0.2 $p('羊肉')=p('牛肉')=0.2$ ,总结一下约束条件为：

P (x)

$P(x)$

s t . p (' 素 食') = 0.6

$st.p('素食')=0.6$

p (' 素 食') + p (' 羊 肉') + p (' 牛 肉') = 1

$p('素食')+p('羊肉')+p('牛肉')=1$
以上就是对最大熵的原理的阐述，其实就是满足约束条件后，其他的尽可能的保持随机，均匀分布。
对我们采集的训练集进行抽象，训练集

T=(x1,y1),(x2,y2),(x3,y3),(x4,y4)T=(x1,y1),(x2,y2),(x3,y3),(x4,y4) $T={(x_1,y_1),(x_2,y_2),(x_3,y_3),(x_4,y_4)}$ ,有了样本数据，可以确定联合分布P(x,y)的经验分布，与边缘分布P(x)的经验分布,分别用

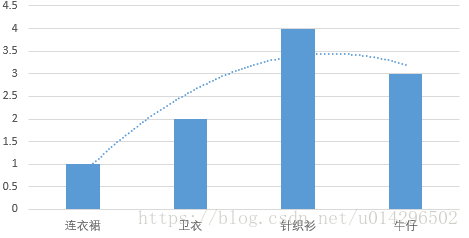
P‘(x,y)与P‘(x)P‘(x,y)与P‘(x) $P^{`}(x,y)与P^{`}(x)$ 表示。什么是经验分布？其实就是根据极大似然估计的思想：已经出现的事件是独立事件，并且是可能性最大的事件。也就是说，我们认为后面的发生都会跟样本差不多。以P(x=’上衣’)为例，如下图：这里写图片描述

根据样本上衣的分布来看，我们可以简单认为女孩的穿衣大概服从正太分布，也就是说P(x)的经验分布为正太分布(该图像为解释经验分布，数据是胡诌的，现在的女孩还是穿牛仔的多点，哈哈)。用一个特征函数，来描述穿衣打扮与吃饭直接的关系:

f(x,y)=0,1f(x,y)=0,1 $f(x,y)=0,1$ ,当穿衣打扮与吃饭满足某个事实时候，取值为1否则取值为0。取这个特征函数的期望：

E (f) = \sum x, y P ‘ (x, y) f (x, y)

$E(f)=\sum_{x,y}P^{`}(x,y)f(x,y)$
根据条件概率公式：

p (x, y) = p (x) p (y | x)

$p(x,y)=p(x)p(y|x)$ 则：

E (f) = \sum x, y P ‘ (x, y) f (x, y) = \sum x, y P ‘ (x) P ‘ (y | x) f (x, y)

$E(f)=\sum_{x,y}P^{`}(x,y)f(x,y)=\sum_{x,y}P^{`}(x)P^{`}(y|x)f(x,y)$
如果模型能够获取训练数据中的信息，那么就可以认为经验分布与真实分布相同即：

① \sum x, y P ‘ (x, y) f (x, y) = \sum x, y P ‘ (x) P (y | x) f (x, y)

$①\sum_{x,y}P^{`}(x,y)f(x,y)=\sum_{x,y}P^{`}(x)P(y|x)f(x,y)$
条件熵的定义为：

H (P) = - \sum x, y P (x, y) l o g P (y | x)

$H(P)=-\sum_{x,y}P(x,y)logP(y|x)$
那么满足所有的约束条件，由公式①我们可以直接引出最大熵模型的定义：

H (P) = - \sum x, y P ‘ (x) P (y | x) l o g P (y | x)

$H(P)=-\sum_{x,y}P^{`}(x)P(y|x)logP(y|x)$
根据最大熵模型的原理，也就是说最大化H(p)得到的P(y|x)概率分布，就可以认为是真实分布，P(y|x)就是我们要学习的模型。（解出这个模型我就不继续深入了，有兴趣的可以看一下李航老师的书，里面有具体的推导），最后我们会解出模型

P (y | x) = 1 Z w ( x ) e x p (\sum i = 1 n w i f i (x, y))

$P(y|x)= \frac{1}{Z_{w}(x)}exp(\sum_{i=1}^{n}w_if_i(x,y))$

Z w (x) = \sum y e x p (\sum i = 1 n w i f i (x, y))

$Z_{w}(x)=\sum_{y}exp(\sum_{i=1}^{n}w_if_i(x,y))$
幸好，有很多包已经为我们解决这件事了，我们只需要将我们采集的数据特征one-hot处理（图没有截全）这里写图片描述

，在训练之前可能需要做特征选择，因为有的女孩懂得如何搭配，比如说穿连衣裙可能就搭配高跟鞋，也就说特征之间可能存在相关性，制作协方差矩阵去掉几个，或者我们想多了，有些特征根本与吃什么无关，比如说“眼影”与“吃饭”之间可能就没有关联，通过person相关系数，对比与标签的相关性，进行特征选择。以上做完之后，你就能得到一个撩妹神奇了，祝你顺利！如果效果不行，请加我微信公共号，让我们共同优化。

最大熵模型教你如何撩妹