圆圈中最后剩下的数（约瑟夫环问题）

最新推荐文章于 2022-03-07 14:37:37 发布

原创最新推荐文章于 2022-03-07 14:37:37 发布 · 696 阅读

0 ·

CC 4.0 BY-SA版权

数据结构和算法专栏收录该内容

50 篇文章

订阅专栏

本文介绍了一个经典的约瑟夫环问题，并提供了一种高效的算法解决方案。通过使用递推公式 f(n,m)，该算法可以在 O(n) 时间复杂度内找到 n 个数字在特定步长 m 下的最后一个剩余数字。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目：0, 1, … , n-1 这 n 个数字排成一个圈圈，从数字 0 开始每次从圆圏里删除第 m 个数字。求出这个圈圈里剩下的最后一个数字。

递推公式：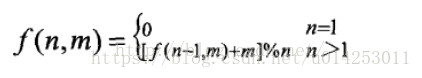
这里写图片描述
f(n,m)表示n个数，每次以步长为m删除，最后剩下的数。可以根据 f(n-1, m)递推求出。

#include <iostream>

using namespace std;
int LastRemaining_Solution(int n, int m)
{
    if (n <1 || m <1)
        return -1;
    int last = 0;
    for (int i = 2; i <= n; i++)
        last = (last + m) % i;
    return last;
}
int main() {
    int n, m;
    cin >> n >> m;
    cout<<LastRemaining_Solution(n, m)<<endl;
    return 0;
}