9.Branch-and-Bound 方法

Branch-and-Bound 方法

Branch-and-Bound（分支限界）是一种用于解决优化问题的算法框架，尤其适用于组合优化问题，如整数规划、旅行商问题（TSP）、指派问题等。该方法通过系统地搜索解空间树来找到问题的最优解或近似解。

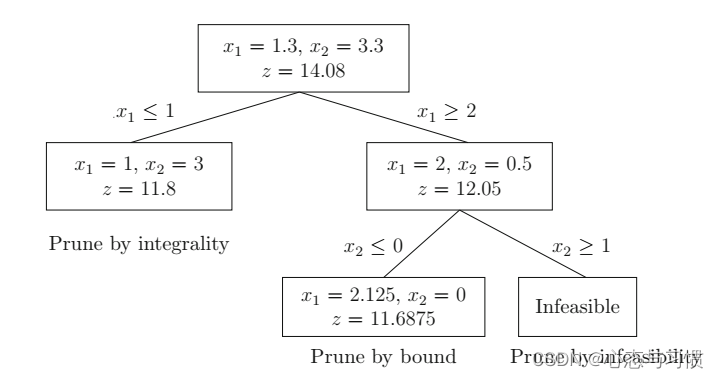
基本概念

Branch-and-Bound 方法的核心在于分支（Branching）和限界（Bounding）两个步骤：

1. 分支：将解空间划分为两个或更多个子空间，通常是通过选择一个变量并为其赋予所有可能的整数值来实现的。这样，原问题就转化为多个子问题。

2. 限界：为每个子问题计算一个界限，这个界限是子问题最优解的一个估计值。对于最小化问题，如果子问题的界限大于当前已知的最优解的界限，那么这个子问题及其所有后代节点可以被排除（剪枝），无需进一步搜索。

工作流程

Branch-and-Bound 方法的工作流程通常包括以下步骤：

• 初始化：选择一个起始节点（通常是问题的完整解空间），计算其界限，并将其加入到待搜索列表中。

• 分支：从待搜索列表中选择一个节点进行扩展，为该节点的每个子节点计算界限，并将这些子节点加入到待搜索列表中。

• 限界：计算每个待搜索节点的界限，并与当前最优解的界限进行比较。如果子节点的界限不优于当前最优解，则该节点及其所有后代可以被排除。

• 更新最优解：如果在待搜索列表中发现一个节点的界限优于当前最优解，则更新最优解。

• 重复分支和限界步骤，直到待搜索列表为空或者找到满意的最优解。

优势和局限性

Branch-and-Bound 方法的优势在于它能够保证找到问题的最优解，并且在搜索过程中通过剪枝减少了不必要的计算。然而，该方法的局限性在于它可能需要搜索大量的节点，特别是在解空间非常大时，算法的运行时间可能会很长。

实际应用

Branch-and-Bound 方法在实际中有着广泛的应用，例如：

• 整数规划：在物流和生产计划中，用于分配资源以最大化利润或最小化成本。

• 旅行商问题（TSP）：在运输和配送中，用于寻找最短的闭合路线，访问一系列城市一次。

• 指派问题：在人力资源管理中，用于将任务有效地分配给可用的员工。

Branch-and-Bound 方法的有效性很大程度上依赖于问题的特性和限界函数的选择，良好的限界函数可以显著提高算法的效率.