矩阵和Tensor
1. Tensor
实际是一个多维的矩阵。

2.矩阵

3.线性代数正确打开方式

3.1 行视图


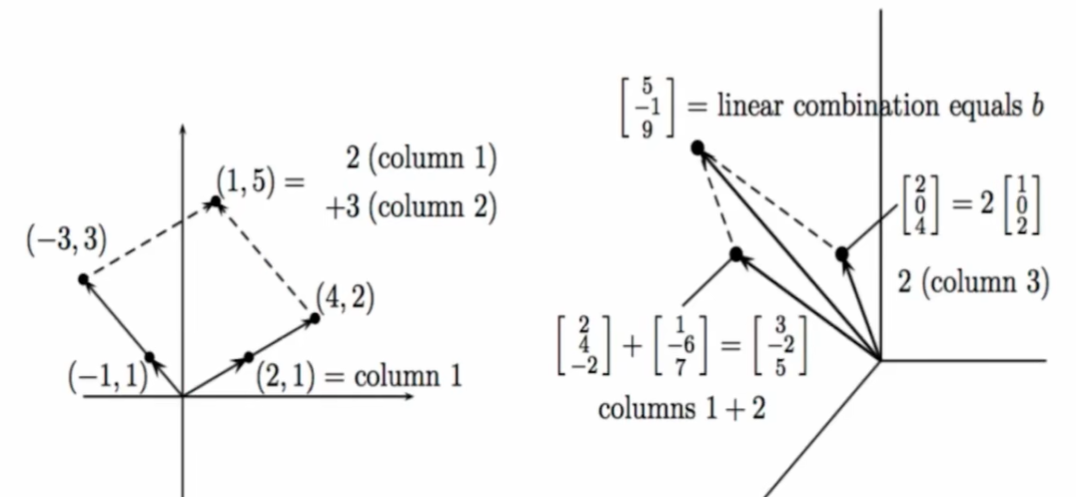
3.2 列视图

4.线性相关和线性无关

5. Span、基和子空间(Subspace)

6.四个基本的子空间
6.1 列空间

6.2 零空间

6.3 行空间

6.4 左零空间

6.5 四个基本子空间的关系
行空间 零空间 正交补
列空间 左零空间 正交补
7.可逆矩阵

8.方阵的特征值与特征向量
λ 是特征值,x是特征向量

9.特征分解
9.1一般矩阵
一般矩阵

- 不是所有的方阵 都能对角化。
- 特征值不一定是实数,还有可能是复数,虚数。
9.2 对称矩阵
对称矩阵。

U是正交矩阵
9.3.1 对称矩阵的性质

9.3.2 特征分解和子空间的关系
A是对称矩阵


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








